[Front page] [Contents] [Previous] [Next] |
Modern Windships; Phase 2
6. Design Loads
Rules, Regulations, Standards, and Other Sources of Information
Short Background on Design Wind Load
Wind Speed Calculations
Wind Pressures
Ship’s Movements
Wind Speeds Updated with Actual Weather Statistics
Loads from Wind Tunnel Measurements of Single Rig
Dynamic Load
Individual Member Forces.
Acceleration Loads
Ice Loads
Sea Water Pressures
Other Loads
Design Loads, Summary
Factors of Safety
To determine the loads affecting the wing mast proved to be quite complicated. Early in the project no measurements or good wind statistics were available. Engineering judgement was used instead. As the project proceeded more and more load data became available, consequently an update of the loads used was called for.
The fact that a sailing ship is subject the fluctuations of both wind and waves makes accurate load prediction difficult. Not only is the mast a flexible tower vibrating on its own with the fluctuating wind load, but the mast foundation and the ship is also moving. The ship accelerates up and down the waves creating both inertia loads and relative wind speeds. The task was to get realistic load values without drowning in safety factors.
Rules, Regulations, Standards, and Other Sources of Information
Before performing any strength analysis it is essential to gather information regarding design loads, factors of safety, allowable stresses and strains etc. In the ship building industry the structure to be constructed is also most often "classed" by a classification society. The requirements of the particular society on scantlings, stability, equipment etc. should be fulfilled.
The WindShip is not designed specifically to any class society, but where applicable the regulation of Det Norske Veritas (DNV) are used. All references can be found in the reference list, see page *.
Short Background on Design Wind Load
The first design load considered was the wind load. Here Lloyds and DNV (see page * section "14. References") converged on which basic design cases should be considered:
- Full sail load, sailing without reef - full wind condition.
- Reefed condition – hard wind.
- Survival, all masts closed – extreme wind.
This also coincided with Ref. 31, though it only considered cases 1 and 2. All rules seemed to have the same basic approach, where the wind is divided into two components. One is a "background" steady component, onto which a fluctuating turbulent component is added. The steady component is often taken as a 10 min. average wind speed. The fluctuating component is then added, often taken as 2-3 sec. gusts.
The size of the gust addition is typically dependent on the surface surrounding the structure. Smooth surfaces will lead to lower turbulence levels and thereby less gusting. On the other hand one might expect higher "steady" components in open landscapes and over sea.
To the above wind speeds the speed of the structure itself has to be added. The movement of the structure can be divided in two components:
- The foundation movement when the ship is making speed over ground as well as rolling and pitching. Heaving was not considered.
- Structural movement due to natural frequency and aero-elastic excitation of the mast. Eigen-frequency excitation can happen when the turbulent component has a frequency near the eigen-frequency of the structure.
The above components can add a significant speed to the local apparent wind components.
One should also consider the wind shearing effect. This means that the wind speed increases with increasing height, as a natural consequence of the ground boundary layer. The slight change of wind direction, which occurs with change of height is normally neglected. The wind shearing effect is normally accounted for by using a logarithmic boundary layer law.
When looking at wind loads it also important to remember the following effects:
| The pressure acts not only as an increased pressure on the upwind side, but also as a decreased pressure on the downwind side. | |
| The turbulent wind load means that one cannot assume the loading to be completely symmetric, its resultant position may fluctuate somewhat over the structures area. | |
| There is a skin friction load to be accounted for. | |
| Structures without sharp corners may be prone to vibrations due to unstable interacting flow patterns in the wake, the so-called "von Karman vortex wake". |
The wind load pressure is calculated using Bernoulli’s equation:
| Equation 5 |
multiplied by some shape/lift/drag factor C. To obtain forces one multiplies the pressure with the exposed area. Notation:
q = pressure [N/m2]
r = density of air » 1.25 [kg/m3].
v = wind speed [m/s].
Wind Speed Calculations
Since wind statistics from the chosen routes were not available until relatively late in the project, some initial estimates were done. When the weather statistics were made available it was obvious that we had been somewhat conservative in our estimates.
The basis wind speed was initially set to 25 m/s. This is the 10 min average wind at 10 meters above sea level. In higher winds the mast should be reefed, folded together. Further calculations on wind speeds can be found in Appendix 4.
Wind Pressures
From the wind speed initially calculated above we could estimate the wind pressures experienced by the wing mast. Further details regarding the wind pressure calculations can be found in Appendix 7.
We concluded that an equivalent sail pressure of 1.7 kPa was the chosen design criteria for the full sail condition. This corresponds to an equivalent wind speed if 29.35 m/s and using a lift coefficient CL of 3.2.
Ship’s Movements
The above calculations did not include the added wind velocities of the ship’s own movements. They can essentially be subdivided into:
- Ship’s speed, sailing at 13 knots in average.
- Rolling and pitching, where the "rolling" is the ship’s movement in the transverse direction around a longitudinal axis. "Pitching" is the movement in the longitudinal direction around a transverse axis.
The addition to the true wind speed is greatest when sailing upwind. From the Velocity Prediction Program (VPP) we know, that the smallest angle at the true wind, where the masts will still give a reasonable contribution to the propulsion, is 40-45° .
At 25 m/s true wind at 45° and a ship’s speed of 13 knots = 6.7 m/s the speed of the apparent wind will be = 30.1 m/s. This corresponds to an addition of 30.1 – 25 = 5.1 m/s. The angle of the apparent wind will be 36° .
Rolling angles were calculated according to DNV, see Appendix 5. From the calculation we had a roll angle of 26.6º, and a rolling period of 16.7 sec. This meant that the ship rolled 4*26.6º = 106º in 16.7 sec. Assuming that the mast top is 60 m above the roll centre this corresponded to sweeping an arc of 1.85 rad, radius 60 m in 16.7 sec. The speed at the top of the wing mast was then 6.6 m/s.
Further calculations indicated that the roll period was 12 sec in ballast, and 20 sec fully loaded. The ballast configuration yielded 9.3 m/s wind speed in the mast top.
Pitching was also calculated according to DNV, see Appendix 5. We got a pitching angle of 5.8º, and a pitch period of 8.3 sec. Assuming the same pitch centre as roll centre we got a wind speed at the mast top of 2.9 m/s.
These calculations were performed without taking the significant aerodynamic damping resulting from adding a sail rig to a ship into account. This damping is specially pronounced in the rolling direction.
If the total effect of simultaneous rolling (9.3 m/s) and pitching (2.9 m/s) should be taken into account the apparent wind speed would be = 38.4 m/s corresponding to an addition of 38.4 – 25 = 13.4 m/s.
This is not reasonable. As the flaps are designed to give way and relieve the wind pressure in case of strong gusts it was decided not to include rolling and pitching and to use the above addition of 5.1 m/s as a standard addition to the true wind speed.
Combining the measured heeling moment coefficient CK with the data obtained from the WindShip hull definition it was possible to determine the heeling angle at different wind speeds. The stability curve for the WindShip can be found below in Figure 32. See also page *, section "WindShip Stability".
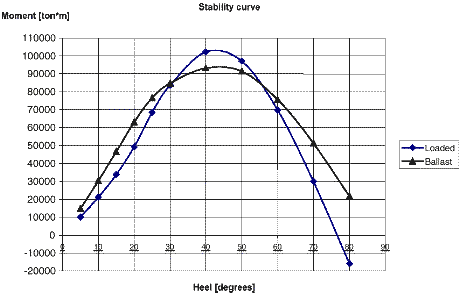
Figure 32. The WindShip stability curve.
Using measurements described below we found the max heeling angle when sailing in 25 m/s wind. With 6 masts we had a heeling moment of approximately 15.500 ton*m. This would incline the WindShip between 5º to 8º depending on loading condition.
Wind Speeds Updated with Actual Weather Statistics
At the beginning of the design phase the design wind speed was set to 25 m/s measured 10 m above the sea level. At this speed the ship should be able to sail with the flaps of the wing mast in their max-lift positions. However, when wind statistics were available later in the design process it became obvious that this choice was unnecessarily high, see Table 3 below. See also page *, section "Weather Routing" and Ref. 8.
| Route nr. | 1 | 2 | 3 | 4 | 5 | 11 | 12 | 13 | 14 | 15 |
| Average wind [m/s] | 5.1 | 5.2 | 3.2 | 7.1 | 5.5 | 8.0 | 7.0 | 5.6 | 5.7 | 5.9 |
| Max 95% [m/s] | 10.8 | 10.8 | 12.6 | 13.4 | 14.0 | 18.1 | 13.9 | 10.8 | 13.6 | 14.0 |
Table 3. Wind statistics on the different trade routes.
The updated wind statistics showed that in the northern Atlantic 95% of the wind speeds were below 18.1 m/s. The rest of the routes had 95% of the wind strengths below 14 m/s. Adding 5.1 m/s to this value from the analysis of the ship’s movements above, the initial basis design wind speed of 25 m/s was still not reached.
As the wind pressure varies directly with the square of the wind speed a reduction of the design wind speed from 25 m/s to 20 m/s would reduce the pressure to 64% of the original. Reducing from 25 to 18 m/s will actually halve the wind pressure.
The majority of the rig components are thin walled sections. As the strength of these sections (the section modulus) vary almost directly with the thickness of the walls, the scantlings calculated for 25 m/s can easily be reduced for a lower design wind speeds:
tred. = t25 m/s ´ (updated design
wind speed)2 / 252 (t = wall thickness)
(This of course is only valid within certain limitations).
We conclude that for the North Atlantic area using 25 m/s as design criteria is probably slightly conservative. For all the other routes 20 m/s would be a more realistic choice.
It is important to note that for the strength calculations of the central steel mast the design wind speeds have been used for the entire mast area (including flaps) regardless of the fact that the flaps will actually give way at a lover value of the wind pressure.
Loads from Wind Tunnel Measurements of Single Rig
In this section the moments and forces measured in the wind tunnel experiments are discussed.
From the measurements in the wind tunnel we do not have the individual forces and moments for each profile. Instead we have the total moments and forces at the mast foot. The measured values can therefore be used for determining the scantlings of the mast. The measured values of the non-dimensional coefficients are averages over the entire wing mast. In the table below the extreme values from runs with a fully deployed wing are summarised.
The measurements were performed with the correct height and turbulence distribution, simulating an open sea environment.
Coefficient |
Angle of attack a [° ] |
Value |
Cl |
21 |
3.2 |
Cd |
66 |
1.7 |
CK |
21 |
3.3 |
CNc/4 |
0-15 |
0.5 |
Table 4. Extreme values of non-dimensional coefficients
Where:
| CL = lift coefficient = | , Equation 6 | |
| CD = drag coefficient = | , Equation 7 | |
| CK = bending moment coefficient = | , Equation 8 | |
| CN = rotating moment coefficient = | , Equation 9 |
And:
| , dynamic pressure, v is the current airspeed. |
a = 23.5 m, force centre of attack.
l = 19.45 m, chord length.
A = 838 m2, area of the wing mast.
r = 1.25 kg/m3, density of air.
The value of CN was relatively constant, depending on the mast foot being located near the aerodynamic centre of the wing mast. Max. bending moment was reached when CL peaked at a = 21° . Max. CD was reached in a stalled configuration.
Using the coefficients measured above the loads on the mast foot were calculated. A design wind velocity 25.0 m/s was used, as stated above. However, since the measurements were not compensated for the wing mast being placed at approximately 15 m above the sea level, this was compensated for by increasing the wind speed. The wind speed thus becomes approximately 26.4 m/s.
The resulting extreme forces can be found in Table 5 below. Note that the values are for different angles of attack a .
Force / Moment component |
Value |
Lift L |
1.17 MN |
Drag D |
0.62 MN |
Bending moment K |
28.3 MNm |
Rotating moment N |
3.55MNm |
Table 5 Forces and moments in the mast foot at 26.4 m/s of wind.
Dynamic Load
To account for dynamic effects from gusts the so called "dynamic gust factor" was calculated in accordance with "Snö och Vindlast" kap 3:322, . The calculations can be found in Appendix 6.
We have Cdyn = 1.93.
The wind loads found in Table 5 above should thus be multiplied with 1.93 in subsequent strength analysis.
Individual Member Forces.
From the measurements above only information regarding loads on the entire mast could be found. An attempt to determine the load on the individual components was made below. These calculations were used to indicate the dimensions of the mechanisms used for steering the flap. The calculations can be found in Appendix 8. See Table 6 for values at a = 21° .
LIft [kN] |
Drag [kn] |
Moment Coefficient CN |
|
SLAT |
262 |
121.3 |
-0.289 |
MAST |
158 |
18.6 |
-0.010 |
FLAP |
654 |
247 |
-0.209 |
Table 6. Estimation of individual forces in the wing mast.
It should be emphasised that these values were rough estimates. Proper measurements should be performed on each member before a more detailed analysis is performed.
Acceleration Loads
Inertia loads occurs both due to acceleration of the foundation, and eigen-frequency excitation, as explained above. Below, loads induced by the ship’s movement are described.
The calculations are performed in accordance with DNV, see Ref. 14. Calculations can be found in Appendix 5.
Using that force equals mass times acceleration, we got the following:
Case 1, vertical and transverse force:
Fvertical = 9.81 * m [N] (normal gravitational load) Equation 10
Ftransverse = (2.95 + 0.044*(h-9.5))*m [N] (transverse load with added rot.) Equation 11
Case 2, vertical and longitudinal force:
Fvertical = 12.9 * m [N] (gravitation with added acceleration) Equation 12
Flongitudinal = 4.51 * m [N] (longitudinal acceleration) Equation 13
where:
m = mass in kg.
h = height above the baseline in metres.
The two load cases do not occur simultaneously. Case 1 was considered most severe since it acts in the "weak" transverse direction of the mast. Thus case 1 was the only load case subsequently used in the FE-analysis described below.
Ice Loads
Ice loads should also be considered, if the WindShip was to operate in conditions where icing can occur. At this stage ice loads were not considered.
Sea Water Pressures
The forward lower panels might be subject to wave loads in extreme weather conditions. The sea-pressure loads were calculated according to DNV, Ref. 14. The pressure to be added to the lowest sails was:
qsea-pressure = 11.5 [kN/m2] which corresponds to approximately 1200 kg/m2.
A lowest allowable design pressure is specified in Ref. 14 as 5 kN/m2.
These pressures are substantial, designing the entire sail and mast to withstand sea pressures would significantly increase their weight and price. Since the mast mechanism is designed to give way in case of overload these loads were not further considered.
Other Loads
As mentioned above there are more loads to consider, like skin friction, von Karman vortex shedding etc. These loads will not be considered here.
Design Loads, Summary
From the above calculations we got the following load cases:
Case |
Wind speed [m/s] |
Design pressure [N/m2] |
Comments |
| 1 - Full drive on all sails | 25.0 design speed 29.3 average panel wind speed |
CL = 3.2. p = 3.2 * ½ * 1.25 * 29.32 = 1.7*103Pa. |
First reefing to be done at 25 m/s of continuos wind at 10 m height. |
| 2 – Reefed condition | above 25.0 | Determined by mast considerations. | |
| 3 – Survival condition | continuos: 55.0 gust: 80.8 |
CD = 1.0 p = ½ * 1.25 * 80.82 = 4.1*103 |
All sails folded and set in the wind direction. |
Table 7. Load cases to be considered.
The loads above are to be multiplied with Cdyn = 1.93
Inertia loads are added by applying the following accelerations:
Fvertical = 9.81 * m [N]
Ftransverse = (2.95 + 0.044*(h-9.5))*m [N]
which corresponds to the normal gravity together with a sideways acceleration of 2.95 [m/s2] and an added rotary inertial acceleration of 0.044 [rad/s2].
The whole mast should start turning at the design wind speed of 25 m/s (with the flaps in the minimum lift position as they will give way already at 20 m/s). When folded and turned into the wind’s eye the wing mast should be able to survive a gust wind speed of 81 m/s.
In the subsequent FEM-calculations only load case 1 was investigated. Load case 2 will have to be monitored during sailing, so that max. bending moment in the mast is not exceeded. The survival condition is basically a bending moment acting in the mast "strong" direction, and was not considered critical for the mast. The mast area facing the wind when reefed is approximately 110 m2, to be compared with approximately 840 m2 for the full mast. Thus the total load will be lower in condition 3 than in condition 1.
Factors of Safety
When using finite elements to check stresses in a construction, a material factor of safety, FoS is normally added. These may vary depending on the rule set being used. For the WindShip DNV was used. The material FoS for composite materials in DNV is rather high and specified to 5,0.
This means that the allowable stresses in the face sheets of the sandwich material becomes:
![]() MPa, (see below for composite material
properties).
MPa, (see below for composite material
properties).
For the steel material the allowable stresses were defined in Table 29.
Using a material FoS of 5 on the core material was not judged necessary, as this is not a material which is made in the manufacturing process of the component. This is in contrast to the laminates, where a high material FoS can be motivated due to human error introduced in the production. The core material FoS was set to 2, allowing for 0.5 MPa in shear. No other factors of safety were used.
[Front page] [Contents] [Previous] [Next] [Top] |