Kolloid-faciliteret transport af glyphosat og pendimethalin
Bilag 9
MIKE SHE AG – Brugermanual
Kolloidmodul
Contents
- 1 Technical Reference Manual
- 1.1 Generation of colloidal particles
- 1.2 Generation of boundary condition
- 1.3 Modification of Macropore Module for MIKE SHE
- 1.4 Transport of colloids
- 1.5 Transport of compounds accounted for in the model
- 1.6 Reactions accounted for in the solver
- 1.7 Process type 3: Sorption (includes colloid-sorption, -filtration and -source)
- 1.7.1 Sorption together with dual porosity
- 1.7.2 Sorption type 1 & 2: Soil- or colloid-sorption
- 1.7.3 Sorption type 3: Clogging
- 1.7.4 Sorption type 4: Filtration of colloid (and species sorbed to colloid)
- 1.7.5 Sorption type 5: Colloid source (detachment of colloid with sorbed species), only UZ matrix and/or SZ mobile phase
- 1.8 Mass balance variables used for "special" processes
- 2 User Guide
- 3 References
1 Technical Reference Manual
This manual presents the theoretical basis for modelling transport of colloids and colloid-facilitated transport in matrix and macropores. The incorporation of colloidal transport in the model includes description of the production of colloidal particles, the transport of these particles through the unsaturated zone, the saturated zone and drains. The module(s) presented herein have been developed for a specific project and therefore may lack some generality.
1.1 Generation of colloidal particles
There are two ways colloids can be generated: 1) colloids can be mobilised at the soil surface in response to rainfall and 2) colloids may be generated through desorption in the soil matrix. Mobilization of colloids in deeper soil structures is usually a smaller amount compared to the mobilization at the soil surface. The actual description of particle mobilization is comparable to erosion modelling. The mobilization of particles from a time-variant pool of potentially mobile soil particles at the surface is proportional to the kinetic energy or squared momentum of the rainwater and a parameter describing the ease with which, particles are detached from the particular soil-type.
Three approaches to modelling of colloid generation can be used:
- a kinetic energy model
- a raindrop momentum model
- A kinetic energy model similar to that of the MACRO-model (Jarvis & Larsson, 1998)
1.1.1 Kinetic Energy Model
Soil detachment by raindrop impact is described based on a kinetic energy model also used in the EUROSEM model by Morgan et al.1998c given by:
![]() (1)
(1)
where DET is the detachment [ML-2T-1], (g/m²/s)
KET is the total kinetic “energy” of the rainfall [MT-3], (g/s³)
k is an index of detachability of the soil [T²L-2], (s²/m²) and
KH is a water depth factor [-].
The total kinetic energy of rainfall can be divided into energy by raindrop impact on the bare ground and energy from rain reaching the surface as leaf drainage:
![]() (2)
(2)
where KEDT is kinetic energy from direct throughfall [MT-3], (g/s³) and
KELD is kinetic energy from leaf drainage [MT-3], (g/s³).
The rainfall energy reaching the ground surface as direct throughfall is estimated as a function of rainfall intensity from an equation derived by Brandt (1989) relating energy to precipitation:
![]() (3)
(3)
where P is rainfall intensity [LT-1], (notice: mm/hour!)
DT is direct throughfall [LT-1], (notice: mm/s!)
The energy of leaf drainage is estimated using the following relationship developed experimentally by Brandt (1990):
![]() (4)
(4)
where PH is effective plant height [L], (m)
LD is leaf drainage [LT-1], (notice: mm/s!)
The model sets the kinetic energy by leaf drainage to zero when the height of the plant canopy is less than 14 cm in order to avoid the otherwise negative values predicted by Equation (4).
The water depth factor KH expresses a decrease in soil detachment with increasing water depth, h (m), due to absorption of energy by the ponding water instead of the soil and a decrease in lateral water jets occurring within the splash crater. Several exponential and power functions have been proposed by Park et al. (1982), Hairsine and Rose (1991) and in EUROSEM by Morgan et al. (1998c), of which three have been incorporated into this model.
The model by EUROSEM assumes an exponential relationship given by:
![]() (5)
(5)
where b is an experimentally derived coefficient [L-1], (1/mm).
The model by Parks relates the water depth factor to median drop size by:
![]() (6)
(6)
where dds is median drop size [L], (m), and is computed by an empirical relation (dds = 1,238·P0,182).
The water depth factor by Hairsine and Rose is similarly to Park’s expression related to median drop size, however using a power function instead:
![]() (7)
(7)
The three models are depicted in Figure 1.1 below as a function of water depth and apart from the shape the curves are clearly very different. The function by EUROSEM decreases very steeply compared to the other two since no account for drop size is made in this formula.
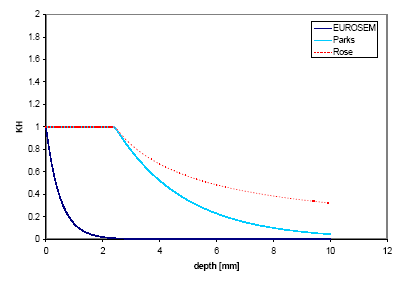
Figure 1.1. Water depth factor functions used in MIKE SHE SE computed for a rainfall intensity of P=40 mm/h.
Figur 1.1. Vanddybdefaktor-funtioner anvendt I MIKE SHE SE beregnet for en nedbørsintensitet på P=40 mm/time.
1.1.2 Rainfall Momentum Model
The description of splash erosion using rainfall momentum is based on a model developed by Styczen and Høegh-Schmidt (1988). The method describes detachment of soil by the momentum of raindrops reaching the bare soil as well as by the momentum of drops falling from the canopy. The expression for soil detachment is given by:
![]() (8)
(8)
where A(e) is a soil resistance factor [T²M-1L-2], (s²/g/m²)
MA is a mulch factor [-]
CM is the ratio of the total squared momentum of drops relative to the squared momentum of drops on bare soil [-]
MR is the squared momentum of drops on bare soil [M²T-3], (g²/s³).
The resistance factor A(e) comprises the soil factors related to the resistance of the soil to erosion such as average energy required to detach one micro-aggregate and the probability that the detached aggregate retains energy for lifting to a water layer. The probability is assumed constant for all sizes of particles for a given soil and A(e) is thus a constant value. The mulch factor is the fraction of soil, which is covered by either mulch, stone and close growing vegetation and thus constitutes areas that are never reached by rainfall. This evidently implies that no erosion due to splash can occur here. The momentum of rainfall MR on bare soil depends on the drop size distribution of the rainfall. For rainfall following the Marshall Palmer distribution, the rainfall momentum is approximately proportional to the intensity of the rainfall lifted to a power given by:
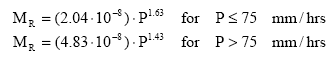 (9)
(9)
The canopy momentum factor CM is a factor expressing the relative effect of vegetation on soil detachment and is actual rain drop momentum from bare soil and vegetated soil given relative to rainfall momentum, i.e.
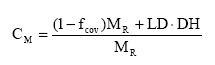 (10)
(10)
where DH is the momentum of drops from the canopy [M²L-1T-2], (g²/m/s²)
LD is leaf drip [L/T], (m/s)
The momentum factor for canopy DH depends on drop velocity, which again depends on drop size and fall height. Velocities have been measured by Epema and Riezebos (1983) for various combinations of drop sizes and water heights and based on this set of data the following relationship is proposed for drop sizes between 4.5 – 6 mm:
![]() (11)
(11)
where the constants a, b, c and d are given in Table 1.1 below.
Table 1.1. Constants used in computation of the vegetation factor DH.
Tabel 1.1. Konstanter anvendt i beregningen af vegetationsfaktoren DH.
| Drop sizes | (mm) | ||||
| Plant Height | 4.5 | 5.0 | 5.5 | 6.0 | |
| < 2 m | a | - | - | - | - |
| b | 0.7954 | 1.1058 | 1.4916 | 1.9601 | |
| c | - | - | - | - | |
| d | - | - | - | - | |
| 2-13 m | a | -0.5 | -0.5 | -0.5 | -0.5 |
| b | 1.2031 | 1.5930 | 2.0692 | 2.5496 | |
| c | -0.12416 | -0.15954 | -0.20184 | -0.23976 | |
| d | 4.33E-3 | 5.44E-3 | 6.70E-3 | 7.68E-3 | |
| > 13 m | a | 3.8647 | 5.4080 | 7.2934 | 9.5310 |
| b | - | - | - | - | |
| c | - | - | - | - | |
| d | - | - | - | - |
The water depth factor KH in equation (8) was defined in equations (5)-(7) and is identical to the formulation used in the kinetic energy model.
1.1.3 MACRO-Model
The original formulation of detachment in the MACRO model is given by:
![]() (12)
(12)
where DET is the particle detachment rate [ML-2 T-1], (g/m²/s)
kd1 is an index of detachability of the soil [T²L-2], (s²/m²)
Ms is the mass fraction of dispersible (movable) particles (g/g soil)
KET is the kinetic energy from Equation (2).
The pool of detachable particle Ms is time-variant according to:
![]() (13)
(13)
where ρs is the soil bulk density [ML-3], (g/m³)
zi is the depth of top-soil influenced by detachment and dispersion, [L], (m)
α is the share of the detached particles that are actually transported away from the soil surface (0 < α < 1)
Rrep is the rate of replenishment of the pool of particles [ML-2T-1], (g/m²/s)
The process of replenishment is not well known (or described) and therefore a simple functional relationship is used to describe the replenishment towards a maximum value Mmax (g/g soil):
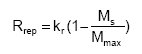 (14)
(14)
where kr is the replenishment rate coefficient [ML-2T-1], (g/m²/s)
The temporal development in the pool of dispersable particles is calculated by analytical integration of (13) leading to:
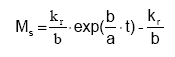 (15)
(15)
where a = ρS ·· zi
![]()
1.2 Generation of boundary condition
The output from the subroutine for calculating detachment is ‘DET’ given in units of mass/area/time. The detachment is then automatically added to the overland component as a source and may pond, infiltrate or run off on the surface.
1.3 Modification of Macropore Module for MIKE SHE
Research showed that it was necessary to perform an adjustment in the code of the Macropore Module for MIKE SHE. The physical water exchange between macropores and matrix was previously only allowed to transport water from the matrix to the macropores and not to uptake water from the macropores into the matrix. Now, water can exchange between both domains defined by empirical first-order linear water transfer coefficients.
1.4 Transport of colloids
Colloid transport is handled as transport of any other species in MIKE SHE Advection-Dispersion (AD). Readers are referred to the manual for MIKE SHE AD for further explanation of the principles applied in the transport algorithm. Apart from the general advective-dispersive transport, specific sink terms for filtration of colloidal particles will apply. Filtration of colloids in macropores is described in Jarvis, 1994 as:
![]() (16)
(16)
where Fmacro is the filtering rate [M L-3 T-1], (g/m³/s).
fref is the reference filter coefficient [L-1], (1/m)
vref is the pore water velocity where fref is measured [L/T], (m/s)
v is the pore water velocity [L/T], (m/s)
nf is an empirical constant
c is the colloid concentration [M/L³], (g/m³)
θ is the water content [L³/L³], (-)
For filtration of colloids in the matrix the same type of expression is used, but the filter coefficient is expected to be significantly higher:
![]() (17)
(17)
where fc is the reference filtering coefficient [L-1], (1/m)
1.5 Transport of compounds accounted for in the model
The colloids, pesticide, and its metabolite can exist in various states (names in parenthesis indicate the names used in the code) in the four domains – the matrix and macropores (UZ) and mobile and immobile water (SZ):
- pesticide dissolved (PDis)
- metabolite dissolved (MDis)
- colloids dissolved (Col)
- pesticide EQ-sorbed to colloids (PEqCol)
- pesticide Kin-sorbed to colloids (PKnCol)
- metabolite EQ-sorbed to colloids (MEqCol)
- metabolite Kin-sorbed to colloids (MKnCol)
- pesticide EQ-sorbed to soil (PEqSrb)
- pesticide Kin-sorbed to soil (PKnSrb)
- metabolite EQ-sorbed to soil (MEqSrb)
- metabolite Kin-sorbed to soil (MKnSrb)
- colloid source of colloids (ColSrc) – only matrix and mobile water!
For the macropores and immobile water the list is the same – except the last state “colloid source sorbed to soil”.
Each of these states is defined as a species in the setup for MIKE SHE AD. The distribution of the pesticide and the metabolite between the various states is handled by a special version of the Sorption-Degradation (SD) module of MIKE SHE. Also the degradation of the pesticide and following formation of the metabolite is handled by that module. The exchange of solute between matrix and macropore is handled by the AD-module for macropore transport as for any other species (see manual for macropore transport).
1.6 Reactions accounted for in the solver
The reactions listed below are solved in four domains:
- unsaturated zone matrix (domain A-UZ)
- unsaturated zone macropores (domain B-UZ)
- saturated mobile zone (domain A-SZ)
- saturated immobile zone (domain B-SZ)
The reactions are shown in Figure 1.2 below.

Figure 1.2. Overview of reactions solved in domain A (UZ matrix / SZ mobile zone) – similar reactions occur in domain B (UZ macropores / SZ immobile zone).
Figur 1.2. Oversigt over reaktioner beregnet I domæne A (UZ-matrice/SZ mobil zone) – lignende reaktioner sker I domæne B (UZ makroporer/ SZ immobil zone).
Each sorption reaction is defined as two reactions; a sorption and a desorption reaction. An equlibrium constant is specified and the correct proportion between the two rates is chosen from a forward rate and the relation Kd = kforward/kbackward. The smallest value of kforward or kbackward is defined as:
Maximum [10 × max (other reaction constants); MinEqSorpRC]
where MinEqSorpRC = 1.9254 ·· 10-4 s-1 (T1/2 = 1 hour)
The filtration processes are only directed from the aqueous phase towards the solid phase. The filtration processes are defined so that:
- filtrated colloids become soil and cannot re-enter the aqueous phase as colloids
- filtrated colloids carrying pesticide or metabolite is converted to pesticide/metabolite sorbed to soil, and hence the pesticide can re-enter the aqueous solution
The degradation reactions are first-order reactions which can be made dependent upon water content and temperature (see the MIKE SHE SD-manual). The total system is solved using an L-stable Rosenbruck with a strongly embedded formula for error control.
1.7 Process type 3: Sorption (includes colloid-sorption, -filtration and –source)
Sorption of dissolved species to soil or colloid can be described as equilibrium (EQ) sorption:
C <-> S1
or combined equilibrium- and kinetic (EQ/Kin) sorption:
S2 <-> C <-> S1
where C : concentration of dissolved species (M/L³)
S1: EQ-sorbed concentration of sorbed species (M/Msoil or M/Mcolloid)
S2: Kin-sorbed concentration of sorbed species (M/Msoil or M/Mcolloid)
In this case the EQ-sorption Fraction (0-1) specifies the fraction of the soil mass allocated for EQ-sorption. The rest (1-Frac) ·· SoilMass is allocated to Kin-sorption. Setting the fraction to 0 results in a pure kinetic sorption process C <-> S2.
1.7.1 Sorption together with dual porosity
In this case the soil mass is divided in two parts, available for sorption from the two domains. The Sorption Bias Factor (Fb, range from -1 to +1) is used to control this division:
Bias factor = 0:
Division proportional to porosities, M1 = M ·· Por1/(Por1+Por2)
Bias factor [0;1]:
More soil is allocated to domain A: M1 = M ·· (Por1+Fb·Por2)/(Por1+Por2)
Bias factor [-1;0]:
Less soil is allocated to domain A: M1 = M ·· Por1 ·· (1+Fb)/(Por1+Por2)
Please notice the definition in UZ and SZ, respectively:
UZ: Domain A = matrix, domain B = macropores
SZ: Domain A = fractures (mobile phase), domain B = matrix (immobile phase)
1.7.2 Sorption type 1 & 2: Soil- or colloid-sorption
Sorption type 1: Equilibrium sorption
Sorption type 2: Combined equilibrium- and kinetic sorption
Linear sorption isotherm (Type of Equilibrium-sorption = 1): S = Kd * C.
| Variable | Description | Data type | Unit for global value |
| K1 | Distribution coefficient (Kd) | First Order Grazing Rate Dependance | m³/g |
| K2 | Not used | - | - |
| K3 | Time constant for kinetic sorption | 1st order rate WQ model | per day |
| K4 | Time constant for kinetic de-sorption if Hysteresis is included | 1st order rate WQ model | per day |
Freundlich sorption isotherm (Type of Equilibrium-sorption = 2): S=Kd * CK2.
| Variable | Description | Data type | Unit for global value |
| K1 | Distribution coefficient (Kd) | First Order Grazing Rate Dependance | m³/g |
| K2 | Freundlich sorption isotherm exponent | Dimensionless exponent | ( ) |
| K3 | Time constant for kinetic sorption | 1st order rate WQ model | per day |
| K4 | Time constant for kinetic de-sorption if Hysteresis is included | 1st order rate WQ model | per day |
Langmuir sorption isotherm (Type of Equilibrium-sorption = 3): S=K1*K2*C/(1+K1*C).
| Variable | Description | Data type | Unit for global value |
| K1 | Distribution coefficient (Kd) | First Order Grazing Rate Dependance | m³/g |
| K2 | Langmuir K2 factor | Dimensionless exponent | ( ) |
| K3 | Time constant for kinetic sorption | 1st order rate WQ model | per day |
| K4 | Time constant for kinetic de-sorption if Hysteresis is included | 1st order rate WQ model | per day |
1.7.3 Sorption type 3: Clogging
Not described here.
1.7.4 Sorption type 4: Filtration of colloid (and species sorbed to colloid)
Notice: In the “Species definition” for the filtration process in the *.xtsf file, both the “Dissolved species” and the “Sorbed species” lines must refer to the name of the colloid species:
GENERAL PROCESS PARAMETERS
------------------- Species definitions
Dissolved species : Colloid
Sorbed species : Colloid
Filtration in UZ matrix was defined in Eq. (17):
![]()
where F: the filtration [M L-3T-1]
fc: reference filter coefficient, [L-1]
c : concentration of dissolved colloid [M L-3]
θ : water content [-]
v : pore water velocity [L T-1]
Filtration in UZ macropores and SZ fractures was defined in Eq. (16):
![]()
where F: the filtration [M L-3T-1]
fref : reference filter coefficient, [L-1]
nf : empirical exponent [-]
vref: the pore velocity at which fref has been measured [L T-1]
v : pore water velocity [L T-1]
| Variable | Description | Data type | Unit for global value |
| K1 | Reference filter coefficient, fc (UZ matrix). Not used for SZ. |
Attenuation | m-1 |
| K2 | Reference filter coefficient, fref (macropores & SZ mobile phase). | Attenuation | m-1 |
| K3 | Reference pore velocity, vref (macropores & SZ mobile phase). | Flow velocity | m/s |
| K4 | Filter exponent, nf (macropores & SZ mobile phase). | Dimensionless exponent | ( ) |
1.7.5 Sorption type 5: Colloid source (detachment of colloid with sorbed species), only UZ matrix and/or SZ mobile phase
Notice: In the “Species definition” for the filtration process in the *.xtsf file, both the “Dissolved species” and the “Sorbed species” lines must refer to the name of the colloid species:
GENERAL PROCESS PARAMETERS
------------------- Species definitions
Dissolved species : Colloid
Sorbed species : Colloid
The source is defined by means of an equilibrium concentration of dissolved colloid and a rate constant:
dCol/dt = Ksrc * (Ceq-Col)
where Col: concentration of dissolved colloid (M L-3)
Ksrc: source time constant (T-1)
Ceq: Equilibrium concentration (M L-3)
Detachment of sorbed pesticide and/or metabolite from soil:
The concentration of pesticide and/or metabolite sorbed on the detached colloid is determined as a specified “soil enrichment factor” multiplied with the corresponding sorbed concentrations.
Notice: The source process is one-way. The time constant is automatically set to 0 if the actual concentration of colloid is higher than the specified equilibrium concentration.
| Variable | Description | Data type | Unit for global value |
| K1 | Source time constant, Ksrc | 1st order rate WQ model | per day |
| K2 | Equilibrium concentration, Ceq | Concentration | µg/m³ |
| K3 | Soil enrichment factor for detachment of sorbed pesticide and/or metabolite from soil. | Dimensionless factor | ( ) |
| K4 | Not used |
1.8 Mass balance variables used for ”special” processes
Sorption of sprayed Pesticide (moving sprayed pesticide to upper node in UZ):
- Sources -> OL (Dissolved Pesticide) (spraying defined as an OL source with Pesticide)
- OL -> Sorp/DeSorp(Dissolved Pesticide)
- OL -> UZ (Sorbed Pesticide)
Colloid detachment from ground surface, including sorbed pesticide and/or metabolite from upper node in UZ:
- Sources -> OL (Colloid)
- UZ -> OL (Sorbed Pesticide and/or Metabolite)
- Colloid-Sorp/DeSorp -> OL (Colloid-sorbed pesticide and/or metabolite)
Colloid filtration, including moving colloid-sorbed pesticide and/or metabolite to soil (listed below for UZ, same for SZ):
- UZ -> Sorp/DeSorp (Colloid)
- UZ -> Sorp/DeSorp (Colloid-sorbed Pesticide and/or Metabolite)
- Colloid-Sorp/DeSorp -> UZ (Sorbed Pesticide and/or Metabolite)
Colloid source (detachment), including moving sorbed pesticide and/or metabolite from soil to detached colloid (listed below for UZ, same for SZ):
- Sorp/DeSorp -> UZ (Colloid)
- Sorp/DeSorp -> UZ (Colloid-sorbed Pesticide and/or Metabolite)
- UZ -> Colloid-Sorp/DeSorp (Sorbed Pesticide and/or Metabolite)
2 User Guide
2.1 The Flow Setup File (<setup>.SHE)
In addition to the usual MIKE SHE parameters, two lines need to be specified in the ”Extra Parameters” menu if macropores are included:
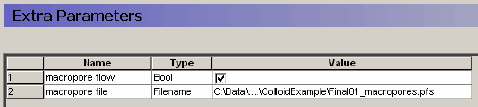
Figure 2.1. Extra Parameters menu in MIKE SHE.
Figur 2.1. Menu for ekstra parameter I MIKE SHE.
For each soil type in the *.pfs file (see Figure 2.2) specified in the ”Extra Parameters” menu, a number of additional parameters regarding macropores need to be specified:
Max_MP_infiltration: Maximum infiltration to macropores to be allowed within a time step. Recommended value is 1 mm or less.
Max_Node_Exchange: Maximum exchange between macropore and matrix to be allowed within a time step for a single UZ-compartment. Recommended value is 0.5 mm or less.
Max_Column_Exchange: Maximum exchange between macropore and matrix to be allowed within a time step for the entire uz-column. Recommended value is 2.0 mm or less.
CloseToWaterTableCorrection: 1:none, 2:Matrix pressure, 3:Hydrostatic pressure.
NO_SOILS: Number of soils included in the *.pfs file.
SoilName: A text string to identify the soil type.
MacroPores: 0: no macropores, 1: macropores.
Porosity: Macroporosity of the soil (-). If the total porosity of the soil is e.g. 0.40 and the macroporosity is 0.02, then the remaining 0.38 is the porosity of the matrix. Please, remember to adjust the matrix porosity of the uz soil property database when including macroporosity.
Ksat: Saturated hydraulic conductivity of the macropores of the soil (m/s).
ConExpo: Exponent in the hydraulic conductivity function for the macropores (-), see manual for Macropore Module. Expected to vary from 2.0 to 6.0.
Psi_Threshold: Matrix threshold pressure at which macropore flow is initiated (m). The value may be below zero as e.g. the air entry point on the retention curve. Expected values could vary from 0.0 m to -0.15 m.
Beta_Mp_Matrix: Water transfer coefficient accounting for water exchange from the macropores to the matrix (m-2).
Beta_Matrix_Mp: Water transfer coefficient accounting for water exchange from the matrix to the macropores (m-2).

Figure 2.2. The macropore *.pfs file can be edited in a text editor.
Figur 2.2. Makropore*.pfs-filen kan editeres i en tekst-editor.
2.2 The Transport Setup File (<setup>.tsf)
The following parameters should be set to true:
Execute all.: T
SZ double por.: T
Overland source: T
In addition to the usual parameters regarding simulation period, time step etc., a total of seven species need to be specified along with a source (pesticide) in the overland (OL) compartment, and a dual porosity mass transfer coefficient in the saturated zone (SZ) to account for mobile/immobile water. The dual porosity is not relevant for the sorbed species.
| Species # | Name | Source | Dual porosity mass transfer coeff. (DP) |
| 1 | Colloid | - | 0.5 |
| 2 | Pesticide | OL, e.g., as a dfs0 file | 0.5 |
| 3 | Metabolite | - | 0.5 |
| 4 | Sorbed-Pesticide | - | 0 |
| 5 | Sorbed-Metabolite | - | 0 |
| 6 | Col-Sorbed-Pesticide | - | 0 |
| 7 | Col-Sorbed-Metabolite | - | 0 |
Particle-facilitated transport is activated by:
- setting a logical Colloid Module = TRUE at the bottom of the transport setup file (.tsf)
- specifying the input for the necessary input parameter for MIKE SHE AD
- specifying the input for the activation module in a file named ‘setupname’.colloid.
The very last lines of the <setup>.tsf file should look like this:
++*+*+*++*++*+*+*++*+*+*+*+*+**+*+*+*+*+*+*+*+*+*+*+*
error if fp control word changed : T
EXTRA TSF FILE : T
Colloid Module : T
max macropore courant number next line : T
max macropore courant number : 0.8
Input for initial conditions, solubility and sources are given as usual, except that source-terms for colloids should be specified in the file ‘setupname’.colloid, see Chapter 2.4.
2.3 The Extra Transport Setup File (<setup>.xtsf)
The following parameters should be set to true or specified:
Sorption: T
Decay: T
Bulk density: 1600 (kg/m³)
A total of 12 processes along with appropriate parameters need to be specified:
| Process # | Name | Process type1) | Sorption type2) | Bias factor3) | K1, K2, K3, K44) |
| 1 | Colloid source | 3 | 5 | ||
| 2 | Colloid filtration | 3 | 4 | ||
| 3 | Kin-sorption of pesticide | 3 | 2 | ||
| 4 | Kin-sorption of metabolite | 3 | 2 | ||
| 5 | Colloid-sorption of pesticide | 3 | 2 | ||
| 6 | Colloid-sorption of metabolite | 3 | 2 | ||
| 7 | Decay of dissolved pesticide | 4 | n/a | ||
| 8 | Decay of dissolved metabolite | 4 | n/a | ||
| 9 | Decay of sorbed pesticide | 4 | n/a | ||
| 10 | Decay of sorbed metabolite | 4 | n/a | ||
| 11 | Decay of col-sorbed pesticide | 4 | n/a | ||
| 12 | Decay of col-sorbed metabolite | 4 | n/a |
1) Process type: 1=not used, 2=not used, 3=sorption og 4=degradation
2) Sorption type: 1=Eq, 2=Eq+Kin, 3=clogging, 4=filtration, 5=source
3) Bias type is further described in the Technical Reference Manual.
4) The constants K1-K4 have different meaning depending on the process and/or sorption type, and are further described in the Technical Reference Manual.
Species dependent unsaturated zone (UZ) data:
| Species # | Name | Matrix-Macropore Mass Transfer coeff. (Beta-MP) |
| 1 | Colloid | 0.5 |
| 2 | Pesticide | 0.5 |
| 3 | Metabolite | 0.5 |
| 4 | Sorbed-Pesticide | Not specified |
| 5 | Sorbed-Metabolite | Not specified |
| 6 | Col-Sorbed-Pesticide | Not specified |
| 7 | Col-Sorbed-Metabolite | Not specified |
2.4 The Colloid Setup File (<setup>.colloid)
If “Colloid Module” is set to true in the <setup>.tsf file, a file containing colloid input data needs to be specified:

Figure 2.3. Example of the *.colloid input file .
Figur 2.3. Eksempel på *.colloid-inputfilen.
Species name: The first seven lines must be included in the input file, however, only species actually included in the simulation need to be specified after the colon “:”.
Conversion factor (g met / g pest): Refers to the amount of g metabolite that is created from each g of pesticide.
Sorption of sprayed pesticide: A logical T/F to determine whether sprayed pesticide (defined as an OL source) should sorb to the soil of the upper node of the unsaturated zone (UZ).
MaxPrecDepthPerTimeStep: Maximum precipitation depth per time step (mm). Controlling the time step of the detachment calculation.
PrecThresholdRate: Precipitation rate requiring its own time step (mm/hour). Controlling the time step of the detachment calculation.
Precipitation distribution: Spatial distribution of the precipitation. Can refer to a dfs2-file or be an integer number.
No. precipitation codes: Number of different precipitation stations in the setup.
Precipitation time series (1-noprec): Temporal variation of the precipitation. Can refer to a dfs0-file or be an integer number. This line is repeated noprec times.
Code for detachment model: Refers to the three options for determining the detachment rates:
1: Kinetic Energy Model
2: Raindrop Momentum Model
3: MACRO-Model
Waterdepth correction: Exponential factor b (1/mm) in Equation (5) in the Technical Reference Manual.
Alpha: Coefficient (0 ≥ α ≤ 1), which determines the fraction of detached particles that infiltrate (See Equation (13) in the Technical Reference Manual).
Parks/Rose/Eurosem: Determines which of the models to be used for calculating the water depth correction.
1: Parks
2: Rose
3: Eurosem
Soil type distribution: Spatial distribution of soil types. Can refer to a dfs2-file or be an integer number.
No. of soil types: Number of different soil types in the setup.
Soil counter (1-nosoil): Soil code used in the soil distribution file. This line is repeated nosoil times.
Detachability, k: Parameter k (g/J) in Equation (1) in the Technical Reference Manual.
A(e): Soil resistance factor A(e) (1/J) in Equation (8) in the Technical Reference Manual. Only relevant for detachment model 2.
Mulch factor, MA: Mulch factor MA (-) in Equation (8) in the Technical Reference Manual. Only relevant for detachment model 2.
Replenishment rate, kr: Replenishment rate coefficient kr (g/m²/s) in Equation (14) in the Technical Reference Manual.
Dry bulk density, ρs: Dry bulk density of top soil ρs (kg/m³) in Equation (14) in the Technical Reference Manual.
Influence depth, zi: Depth of top-soil influenced by detachment zi (m) in Equation (13) in the Technical Reference Manual.
Maximum detachable soil, Mmax: The maximum amount of detachable soil particles Mmax (g/g soil) in Equation (14) in the Technical Reference Manual.
Sorption enrichment factor: For calculation of concentration of pesticide and metabolite sorbed to detached colloid (surface or soil source) = factor × concentration of pesticide and metabolite sorbed on soil.
Vegetation distribution: The distribution of vegetation in the model area is either specified with a single grid code value, if the same vegetation is present in the entire model area or by a dfs2-file containing a number of grid codes, each one representing a specific vegetation type. Each vegetation type is characterised by a number of different properties such as plant cover, plant height, angle and shape. The different plant properties are described in the following sections and must all be specified for each vegetation type.
No. veg types: The total number of plant types in the model.
Veg counter (1-noveg): The vegetation type code is an integer value representing a specific vegetation type, which is initially specified in the before mentioned map file. NB: Must be numbered 1, 2, …, No. veg types.
Cover: The density of vegetation is expressed by the spatial fraction of plant cover, which is dimensionless (0 < cover < 1). Can refer to a dfs0-file or be an integer number.
ICmax: ICmax is the maximum volume of interception by plant cover and is given as a water depth in [mm]. Can refer to a dfs0-file or be an integer number.
Plant height: Effective plant height is used for computing the energy of leaf drainage in Equation (4) [m]. Can refer to a dfs0-file or be an integer number.
Plant angle: The plant angle is given in degrees.
Plant shape: Two different shapes of vegetation have been incorporated into the model. One type (1) represents grass or grass like vegetation and the other type (2) covers all other kinds of vegetation. The shape of the plants is of importance in computing stemflow. For grasses or vegetation with mean diameters smaller than the mean diameter of the drops, gravity plays an important role as opposed to other types of vegetation.
Canopy raindrop size: Canopy raindrop size is important in computing detachment by splash in relation to the computation of the water depth factor, see chapter 3.1.9. The unit is [m].
3 References
Brandt, C. J. (1989). The size distribution of throughfall drops under vegetation canopies. Catena 16, pp. 507-524.
Brandt, C. J.(1990). Simulation of the size distribution and erosivity of raindrops and throughfall drops. Earth Surf. Proc. Landf., 15, 687-98.
Epema, G.F. and Riezebos, H.Th. (1983). Fall velocity of waterdrops at different heights as a factor influencing erosivity of simulated rain. In: de Ploey, J. (Ed.): Rainfall simulation, runoff and soil erosion. Catena Supplement 4, Braunschweig 1983, 1-18.
Hairsine, P.B. and Rose, C.W. (1991): Rainfall Detachment and Deposition: Sediment Transport in the Absence of Flow-Driven Processes. Soil Sci. Soc.Am.J., Vol 55: 320-324.
Hairsine, P.B. and Rose, C.W. (1992). Water Erosion Due to Overland Flow Using Physical Principles. 1. Sheet Flow. Water Resources Research, Vol 28 (1): 237-243.
Hansen, S., Jensen, H.E., Nielsen, N.E., and Svendsen, H. (1990). Daisy-soil plant atmosphere system model. Technical Report A10, Miljøstyrelsen.
Jarvis, N. (1994). The MACRO model – Technical description and sample simulations. Reports and Dissertations, Vol, 19, 51 pp. Department of Soil Sciences, Swedish University of Agricultural Sciences, Uppsala.
Jarvis, N, and Larsson, M. (1998). The MACRO Model (Version 4.1), Technical Description, SLU, Dep. of Soil Sciences, Uppsala.
Morgan, R.P.C., Quinton, J.N., Smith, R.E., Govers, G., Poesen, J.W.A., Auerswald, K., Chisci, G., Torri, D., Styczen, M.E. (1998). The European Soil Erosion Model (EUROSEM): Documentation and user guide. Cranfield university, version 3.6.
Park, S.W, Mitchell, J.K., and Scarborough, J.N. (1982). Soil Erosion Simualtion on Small Watersheds: A modified ANSWERS Model. Transactions of the ASAE, 25(6):1581-1588.
Styczen, M. og Høeg-Schmidt, K. (1988). A new description of splash erosion in relation to raindrop sizes and vegetation. In: Morgan, R.P.C. and Rickson, J. (Eds) Erosion assessment and modelling. Proceedings of a workshop held in Brussels, Belgium, 2-3 Dec. 1986. Commission of the European Communities, EUR 10860.
Wùsten, J.H.M., Lilly, A., Nemes, A., and Le Bas, C. (1998). Using existing soil data to derive hydraulic parameters for simulation models in environmental studies and land use planning. Report 156, Agricultural Research Department, Wageningen, The Netherlands.
Version 1.0 Februar 2007, © Miljøstyrelsen.