| Front page | | Contents | | Previous | | Next |

Water Prices in CEE and CIS Countries. Volume I: Main Text

Appendix 9
Estimation of Willingness to Pay

Estimation of a utility function

From the answers of the stated preference questions a utility function can be estimated. The utility function evaluates the alternatives by tariff and service characteristics.

The theoretical approach to the estimation of willingness to pay higher tariffs is that of microeconomic consumer theory. In consumer theory, individual consumers choose consumption bundles to maximise utility. In stated preference games, the respondent is asked to choose an alternative between two alternatives, A and B, so this is a discrete choice. Letting U represent the utility function respondent i will choose the alternative that implies the highest utility:

The alternatives are described by a number of attributes, x₁, x₂,..,x_k, and these attributes are different for each respondent and each choice. The choice of the consumer reveals the consumer's preferences among the alternatives.

A probability model is used in order to allow for uncertainty. The probabilistic model is used in order to be able to allow effects of unobserved variation among the respondents and to take pure random choices into account as well as errors due to measurement or incorrect information. The random utility approach was formalised by Manski (1977)²⁶. Let V_i be the random utility of consumer i:

Here represents U_i the observed part of the respondents i's observed utility while e_i represents the unobserved or random part. The unobserved part, e_i, is assumed to be independently and identically distributed. When uncertainty is introduced, the choice is treated as a random variable, and the choice probability of alternative A then equals the probability that the utility of alternative A is greater than the utility of alternative B.

Letting P denote a probability, this can be written as:

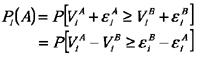
In other words, the choice probability of alternative A is a function of the differences between alternative A and alternative B.

In order to estimate the model, a probability function and functional form of the utility function must be specified. The cumulative logit function, L(), is applied and the utility function is assumed to be of a simple linear form. The probability of choosing A can then be written as follows:

where   etc. and the standard deviation is normalised to 1. In order to take heterogeneity among respondents into account, socio-economic variables are allowed in the model. The socio-economic variables reflect the different preferences about the attributes included in the game, and are included by letting the coefficients of the utility function vary for different groups of respondents. Let s denote a variable defining socio-economic groups such that si denotes the membership of respondent i. Hence, the coefficients for the attributes in the games are different according to the membership of the respondent.

The model is estimated by maximum likelihood. This estimation method gives unbiased and efficient estimates. The method is described e.g. in Greene (1993)²⁷.

Results of the Stated Preference games

The estimated parameters are evaluated with standard statistical tools and common sense. The t-statistics is used to test if a parameter is significantly different from zero - this is the case when the t-statistic is greater than 1.645 for a single sided test and 1.96 for a double sided test.

Calculation of the willingness to pay

The willingness to pay is calculated from the parameter values. This is done by dividing the parameter for the service level(s) of interest by the tariff parameter. By this method the value of a service level is measured in the same units as the tariff.

Uncertainty of the WTP

The standard deviation of the willingness to pay estimates cannot be obtained directly when calculating the WTPs. Two methods are possible to obtain standard deviations: Monte Carlo simulation or bootstrapping. Applying the former solution one has to make an assumption of the distribution that the estimates follow and usually, the normal distribution is assumed. The bootstrap is preferable, since the empirical distribution is used and any assumptions on the distribution can be avoided.

Bootstrapping is sampling with replacement, cf. e.g. Davidson and MacKinnon (1993). From the original sample one observation is picked, registered and replaced. This is done until one has a new sample consisting of the same number of observations as in the original sample. From this new sample a new set of parameter estimates is obtained. This procedure is iterated a large number of times and in this way one can calculate empirical standard deviations, lower and upper bounds of the willingness to pay estimates.

| Front page | | Contents | | Previous | | Next | | Top |