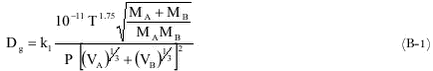| Front page | | Contents | | Previous | | Next |

Dry deposition and spray drift of pesticides to nearby water bodies

Appendix B. Viscosity of air and water and estimation of diffusivity of pesticides in air and water

Diffusivity of gaseous pesticides in air

The diffusivity of a gas in air can be estimated by the method of Fuller, Schettler and Giddings (FSG method) (Lyman et al., 1982). It is most accurate for non-polar gases at low to moderate temperatures. Its accuracy is poorest for polar acids (12%) and glycols (12%) and minimal errors are found for aliphatics (4%) and aromatics (4%) (Lyman et al., 1982).

The FSG method is based on the following equation:

where:
D_g = diffusivity in air(m² s^-1)
T = temperature (K)
P = pressure (atm)
V = molar volume based on the method developed by Fuller et al. (1966) (m ³ mol^-1)
M = molecular weight (g mol^-1).
k₁ = constant necessary to obtain the right dimensions. Its value is 1.0 and its dimension is 

The subscipts A and B in (B-1) refer to the air and the gaseous pesticide, respectively. M_A is 28.97 g mol^-1 and VA is 20.1× 10^-6 m³ mol^-1. V_B can be estimated from the chemical structure of the molecule using the increments listed in Table 1:

where ni is the number of atoms of kind i and VB,i is the volume increment cause by atom i. A correction has to be made to the sum in case of aromatic and heterocyclic rings are present.

Table 1.
Atomic and structural diffusion volume increments V_B (m³ mol^-1) (Fuller et al., 1966).
Tabel 1.
Atom og andre strukturelle diffusions volume inkrementer V_B (m ³ mol^-1) (Fuller et al., 1966).

Atom	VB
C	16.50× 10-6
H	1.98× 10-6
O	5.48× 10-6
N	(5.69× 10-6)
Cl	(19.5× 10-6)
S	(17.0× 10-6)
Aromatic and hyterocyclic rings	-20.2× 10-6

Values in parentheses are based upon few data points (Fuller et al., 1966).
(Reprinted with permission from Fuller et al. (1966). Copyright 1966 American Chemical Society)

For chemicals not listed in Table 1, VB can be estimated as 85-90% of the LeBas volume V_B‘ . In the following calculations we have used V_B = 0.875VB‘ . V_B‘ can be found from Table 2.

Click on the picture to see the html-version of: ‘‘Table 2‘‘

V_B‘ is calculated from the increments in the same fashion as V_B. It should be noted that there are no values of V_B or V_B‘ for phosphorous. This means that it is not possible to estimate the diffusivity in air for organophosphorous pesticides with this method.

The method mentioned above is somewhat complicated. A more simple method was developed here where the diffusivity at one temperature and pressure is estimated from the molecular weight alone. The idea behind this is that the molar volume is proportional to the molecular weight. First the diffusivity was calculated with the FSG method for 11 pesticides with different molecular weights between about 100 and 500 g mol^-1. The following expression was found to give a good description for the relation between Dg and MB at 298.15 ° K and 1 atmosphere:

In this equation D_g,298.15, 1 is in m² s^-1 and M_B is in g mol^-1; k₂ is a constant necessary to obtain the right dimensions. Its value is 1.0 and its dimension is

It would be possible to derive a slightly better fit with a more complicated relation than was used here. It was, however, decided that this was not necessary in view of the uncertainty in other factors in the model in which D_g is used. D_g can be calculated for other temperatures (and pressures) using the relation of B-1:

where Trefis 298.15° K and Pref is 1 atmosphere.

Table 3 shows the results of both methods and their difference. The average absolute difference between the two methods is 5.0 %, which is very reasonable. The results are also shown in Figure 1.

Table 3.
Diffusivity in air at 298.15 ° K and 1 atmosphere calculated with the FSG method and the simple method.
Tabel 3.
Diffusionskoefficient i luft ved 298.15 ° K og 1 atmosfære beregnet med FSG-metoden og den simple metode.

Figure 1. Comparison of the diffusivity in air calculated with the FSG method and the simple method.
Figur 1. Sammenligning af diffusionskoefficienten i luft beregnet med FSG-metoden og den simple metode.

Diffusivity of pesticides in water

The diffusivity of pesticides in water can be estimated with the method of Hayduk and Laudie (Lyman et al., 1990):

where:
D_w = diffusivity in water (m² s^-1)
η_w = viscosity of water (which is a function of temperature) (kg m^-1 s^-1); for sea water the viscosity of sea water should be used.
V‘_B = LeBas molar volume (m³ mol^-1)
k₃ = constant necessary to obtain the right dimensions. Its value is 1.0 and its dimension is

Eq. B-5 does not include a temperature term, since temperature dependence is incorporated in the viscosity term. In section 1.3 of this appendix the viscosity of water is given as a function of temperature for freshwater and sea water (also as a function of salinity).

The method mentioned above is somewhat complicated. A more simple method was developed where the diffusivity in pure water (freshwater) at one temperature is estimated from the molecular weight alone. The idea behind this is that the molar volume is proportional to the molecular weight. First the diffusivity was calculated with the Hayduk and Laudie method for 11 pesticides with different molecular weights between about 100 and 500 g mol^-1. The following expression was then found for the relation between D_w and M_B 298.15 ° K:

In this equation D_w,298.15 is in m² s^-1 and M_B is in g mol^-1. k₄    = constant necessary to obtain the right dimensions. Its value is 1.0 and its dimension is

The diffusivity of the gaseous pesticide D_sw(S,T) for (sea) water at temperature T (° K) and salinity S (pro mille) can be calculated from the following relation, which is derived from (B-5):

where: η_w(0,298.15) is the viscosity of pure water at 298.15 ° K and η_w(S,T) is the viscosity of (sea) water at salinity S and temperature T.

Table 4 shows the results of both methods and their difference. The average absolute difference between the two methods is 5.7%, which is quite reasonable. The results are also shown in Figure 2.

Table 4.
Diffusivity in water at 298.15 ° K calculated with the FSG method and the simple method.
Tabel 4.
Diffusionskoefficient i vand ved 298.15 ° K beregnet med FSG-metoden og den simple metode.

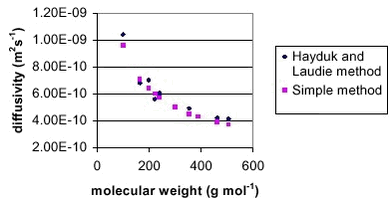
Figure 2. Comparison of the diffusivity in water calculated with the Hayduk and Laudie method and the simple method.
Figur 2 Sammenligning af diffusionskoefficienten i vand beregnet med Hayduk og Laudie metoden og den simple metode.

Dynamic viscosity and kinematic viscosity of air

The kinematic viscosity of air is a function of the dynamic viscosity of air and the density of air. For that reason the density of dry air has to be calculated (Pruppacher and Klett, 1997):

where:
ρ_a = density of dry air (kg m^-3)
M_da = molecular weight dry air (28.9644 g m^-2)
P = pressure (atm)
R = gas constant (8.2057× 10^-5 atm m³ mol^-1 K^-1)
T = temperature (K)

The dynamic viscosity of air between -50° C and +50° C is given by (Pruppacher and Klett, 1997):

where:
η_a = dynamic viscosity of the air (kg m^-1 s^-1)
t = temperature (° C)

The kinematic viscosity of air ν_a (m² s^-1) is:

Viscosity and kinematic viscosity of (sea)water

The kinematic viscosity of (sea) water at 1 atmosphere is a function of the viscosity of water, but also of the density of water and for seawater also of the salinity. For that reason the density of (sea) water has to be calculated. The density of pure (fresh) is (kg m^-3) (Sündermann, 1986):

where ρ_w is the density of pure (fresh) water (kg m^-3) and t is the temperature (° C).

The density of seawater at 1 atmosphere as a function of the temperature and the salinity is now given by (Sündermann, 1986):

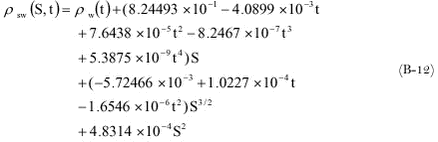
The above equation is valid for salinities between 0 and 42 pro mille and a temperature between –2 and +40 ° C.

The viscosity of pure water is given by (Sündermann, 1986):

where t is the temperature (°C) and ηw(20) = 1.002×10^-3 (kg m^-1 s^-1). This equation is valid for 1 atmosphere and a temperature range of 10 to 70 °C.  

The viscosity of sea water at 1 atmosphere can be obtained from (Sündermann, 1986):

In this equation η_sw(S,t) is the dynamic viscosity of sea water at 1 atmosphere at salinity S (pro mille) and temperature t(° C). Cl_v is the volume chlorinity, which is related to salinity by (Sündermann, 1986):

This is valid for salinities between 0 and 40 pro mille and temperatures between 5 and 25 °C.

The kinematic viscosity of (sea) water at 1 atmosphere νsw (m² s^-1) is defined by:

Note: the equations for sea water can also be used to calculate the kinematic viscosity of freshwater by putting a value of 0 for the salinity in the equations.

References

Fuller, E.N., Schettler, P.D., Giddings, J.C. (1966) A new method for prediction of binary gas-phase diffusion coefficients. Ind. Eng. Chem. 58, 19-27.

Lyman, W.J., Reehl, W.F., Rosenblatt, D.H. (eds.) (1990) Handbook of chemical property estimation methods, American Chemical Society, Washington DC, USA.

Pruppacher, H.R., Klett, J.D. (1997) Microphysics of clouds and precipitation. Kluwer, Dordrecht, The Netherlands.

Reid, R.C., Prausnitz, J.M., Sherwood, T.K. (1977) The properties of gases and liquids, 3rd. edition, McGraw-Hill, New York.

Sündermann, J. (ed.) (1986) Landolt-Börnstein, Numerical data and functional relationships in science and technology. New series. Group V: Geophysics and space research, Vol. 3: Oceanography, subvolume a. Springer, Berlin, Germany.

| Front page | | Contents | | Previous | | Next | | Top |