| Front page | | Contents | | Previous |

Fate of Pyrethroids in Farmland Ponds

Appendix A

Investigation of the interrelationship between the Rsed and Dsed values

The water column concentration is assumed constant in order to keep the analytical solution of the differential equation simple. This gives the following initial and boundary conditions

c_d,sed=co, for x=0, t>0 (A.1)

c_d,sed=0, for x>0, t=0 (A.2)

where co is a constant value concentration in the water column and c_d,sed is the dissolved concentration in the sediment pores. The constant value for co is in conflict with the observed concentration vs. time relationships. However, the influence from the Rsed and Dsed values on the sediment uptake will be quite similar for this situation compared to the situation having non constant co values.

Eq. 6.17, combined with the Eqs. A.1 and A.2 can be solved using a Laplace transformation (Crank, 1975, pp. 20) as

(A.3)

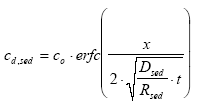
where erfc is a standard function called the complementary error function, which is defined as

(A.4)

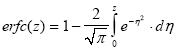
It is only possible to solve this integral equation numerically, but the equation can be rewritten to the following series

(A.5)

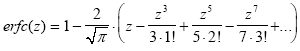
For small positive values of z (z<<1) the higher order terms in Eq. A.5 will vanish and an approximately equation turns out as

(A.6)

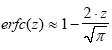
Infinitely close to the surface ( x → 0 ) the z value in Eq. A.5 is small, thus, Eq. A.6 can replace A.5. Therefore, close to the surface, Eq. A.3 becomes

(A.7)

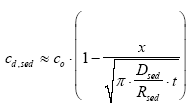
The flux (μg/(m²h)) into the sediment by diffusion is described as

(A.8)

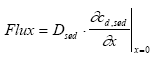
differentiation of A.7 with respect to x and insertion of the solution into A.8 yields equation A.9

(A.9)

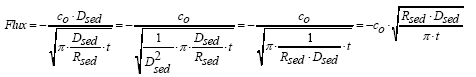
From Eq. A.9 it can be seen that the flux into the sediment depends on the product between R_sed and D_sed.

| Front page | | Contents | | Previous | | Top |

Version 1.0 September 2004, © Danish Environmental Protection Agency