|
Noise from offshore wind turbines 3 Sound Propagation from Offshore Wind Turbines
3.1 IntroductionThe purpose of this section is to illustrate the differences to be expected between sound propagation from offshore wind turbines and land-based wind turbines. The illustration is based on existing sound propagation models described in the literature and calculations made with these models for typical spectra of wind turbines as well as on other knowledge of sound propagation. 3.2 Literature on Sound Propagation ModelsThe sound propagation from offshore wind turbines is only described in the literature to a limited extent. In an earlier article of Hubbard and Shepherd [4] the basic aspects of sound propagation from land-based wind turbines are described. The article contains results from measurements of noise from wind turbines performed in a desert area where the sand surface will be hard at least at the low frequencies and thus correspond to a water surface. The article describes the effect of meteorological refraction by the formation of shadow zones in upwind and sound channelling at low frequencies in downwind. It is concluded that the measurements in downwind at high frequencies (630 Hz) show good correlation with spherical propagation (6 dB reduction per doubling of distance) plus air absorption, where measurements at low frequencies (8-16 Hz) show better correlation with cylindrical propagation (3 dB reduction per doubling of distance). Almost at the same time as the publication of [4] the Danish Ministry of Environment published "Bekendtgørelse om støj fra vindmøller" ("Government Order on Noise from Wind Turbines") [2] describing a method for determination of the sound pressure level at a height of 1.5 m above ground at the nearest neighbour. The sound pressure level is calculated according to [2] by Equation (1).
where LWA,ref is the sound power level of the turbine, l is the distance between the turbine base and the receiver, h is the hub height, and ΔLa is the air absorption. The number 8 in the equation indicates that the ground increases the sound pressure level by +3 dB relatively to free field corresponding to hard ground. According to [2] ΔLa can be calculated with a simple attenuation coefficient of 0.005 dB/m or with a little more advanced octave band method. In case of large propagation distances the two methods can result in considerable differences. In 1998 the EU Project JOR3-CT95-0065 on immission of noise from wind turbines [5] was finalized. The project dealt among others with the elaboration of a prediction method for the sound propagation and validation of the model with measurements of sound propagation from a number of wind turbines. For one wind turbine the sound propagation was over water. The acoustical principles used in the propagation model correspond by and large to the principles applied in Nord2000 ([9] and [10]), but the model is only valid for level ground, whereas Nord2000 is a general propagation model. The model gave good agreement with the measurements, but the measurements only cover distances up to 600 m and in the case with propagation over water only up to 350 m. In 2001 Naturvårdsverket in Sweden published a report [6] with a proposal for a Swedish prediction method for noise from wind turbines with sound propagation both over ground and water. The proposal was based on a literature study [7]. For land-based wind turbines and a propagation distance below 1000 m the A-weighted sound pressure level is calculated according to Equation (2), which corresponds to the Danish method given in Equation (1). The calculation of ΔLa also corresponds to the Danish method with a simple attenuation coefficient of 0.005 dB/m. For land-based wind turbines and a propagation distance above 1000 m the A-weighted sound pressure level is calculated according to Equation (3), which corresponds to the Danish method with a reduction of 2 dB (ground effect of +1 dB relatively to free field instead of +3 dB). The calculation of ΔLa in Equation (3) has a resemblance to the Danish octave band method, but the attenuation coefficients in the octave bands are not the same, and the method goes down to 63 Hz, where the Danish method ignores air absorption below 250 Hz. For offshore wind turbines and a propagation distance below 200 m the A-weighted sound pressure level is calculated according to the same method as used for land-based wind turbines in Equation (2). For propagation distances above 200 m the A-weighted sound pressure level is calculated according to Equation (4), where the calculation of ΔLa corresponds to the octave band method for land-based wind turbines with propagation distances of above 1000 m. The term 10log(r/200) in the equation means that the propagation gives an attenuation of 3 dB per doubling of distance instead of 6 dB (cylindrical instead of spherical propagation). In [6] it is stated that the prediction model is based on very few measurement data and produces the upper limit of the noise. This comment may suggest doubt as to whether cylindrical sound propagation already begins at distances of 200 m. Although not quite clear from the report, the Swedish method seems to be based on experiences from relatively low wind turbines (hub height of 20 to 40 m). Ground < 1000 m, water < 200 m:
Ground > 1000 m:
Water > 200 m:
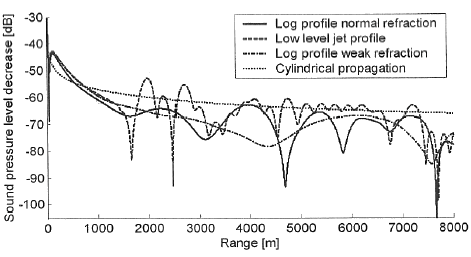
In 2003 sound propagation from offshore wind turbines was theoretically treated in a PhD study [8]. The emphasis of the study is laid on advanced mathematical methods for calculation of sound propagation in an atmosphere with refraction. Calculations of the sound pressure level from a 65 m high wind turbine as a function of propagation distance up to 8000 m have been made for different meteorological conditions. The calculations were, however, only made for low frequencies (about 50 Hz). The calculations demonstrate that spherical propagation is a good approximation at distances below 3000 m for a logarithmic wind profile and wind speeds of up to 8 m/s measured 10 m above ground. At strong refraction (15 m/s) this distance decreases a little, but is still larger than 2500 m. At special wind conditions with a low level jet (approx. 15 m/s at 200 m height) and a strong increase in wind speed from 100 to 200 m height, it has been demonstrated that sound channelling occur down to below 2000 m. The decrease in sound pressure level with distance at 50 Hz, calculated in [8], is shown in Figure 9 for weak refraction (3 m/s), normal refraction (8 m/s), and for the situation with a low level jet and compared with the expected result assuming cylindrical propagation. Figure 9 The decrease with distance of the sound pressure level from a 65 m high wind turbine at propagation over water under three different meteorological conditions and comparison with expected values assuming cylindrical propagation.
The general prediction method, Nord2000, described in [9] and [10] is expected to be well suited for calculation of sound propagation from wind turbines. The method is developed for prediction for all non-extreme types of weather and for any kind of ground. For sources placed at low height as e.g. roads and railways the method will have a limited accuracy at distances above approx. 1000 m, but in cases with sources placed at high height a satisfactory accuracy is expected considerably above 1000 m. The method includes the effect of meteorologically determined shadow zones and the effect of multiple reflections from the ground (which is called sound channelling or cylindrical propagation in the studies referred to above). The method for multiple reflections in Nord2000 has, however, a weakness which was not solved in connection with the preparation of Nord2000. It was concluded in [10] that the contribution from the many rays of multiple reflections shall be added incoherently (on an energy basis) at high frequencies and coherently (on a pressure basis) at low frequencies. It was, however, not possible to find a reliable principle for the transition between coherent and incoherent summation, which will depend on the geometrical and meteorological conditions. As the emphasis in the Nord2000-work was laid on noise from sources at low height as e.g. roads and railways where multiple reflections can occur at relatively short distances (above 200-300 m) and where the A-weighted noise levels are determined by the high frequencies, it was decided as a temporary solution to use incoherent summation in the whole frequency range. As to wind turbines the situation is, however, different as multiple reflections do not occur until at considerably larger distances (above 2000-3000 m) where the immission spectrum will be dominated by low frequencies due to air absorption, and thus the low frequencies will determine the A-weighted sound pressure level. Therefore, when applying Nord2000 at distances above approx. 1000 m, it can be necessary to solve the problem with the transition from coherent to incoherent summation, or to consider as a temporary solution to use coherent summation in the whole frequency range. 3.3 Calculation of Ground EffectTo illustrate the differences to be expected between the sound propagation of offshore wind turbines and land-based wind turbines, a number of calculations were made with the propagation models described in Section 3.2. At first calculation of the ground effect of sound propagating from a wind turbine with a hub height of 30 m at distances from 100 to 10,000 m was made. A height of 30 m corresponds approximately to the heights which are the basis of the Danish and Swedish method referred to in Section 3.2 (the typical height of a wind turbine were 30 to 40 m at the time the methods were developed). In the calculations with Nord2000 the source spectrum of a Modern 2MW wind turbine measured at a wind speed of 8 m/s at 10 m height has been used (Figure 10). The ground effect has been defined as the difference between the A-weighted sound pressure level and the A-weighted free-field sound pressure level. When calculating the sound pressure levels the air absorption corresponding to an ISO-atmosphere (15° C and 70% RH) has been used. At propagation over ground a flow resistivity of 200,000 Nsm-4 is assumed corresponding to grass-covered ground and at propagation over water a flow resistivity of 20,000,000 Nsm-4 corresponding to a hard surface. Figure 10 Source spectrum for a modern 2MW wind turbine measured at a wind speed of 8 m/s at 10 m height.
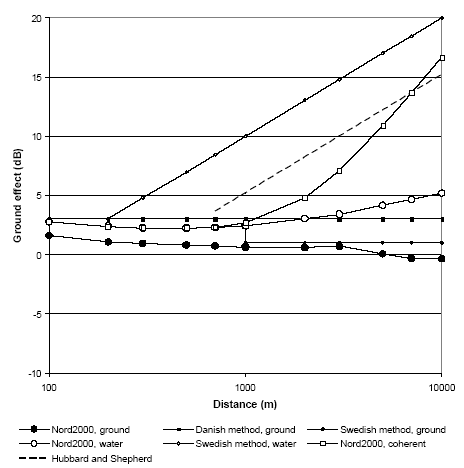
In Figure 11 the following results from calculations or measurements are shown:
Figure 11 Ground effect for a wind turbine with a hub height of 30 m predicted according to different models at propagation both over ground and water.
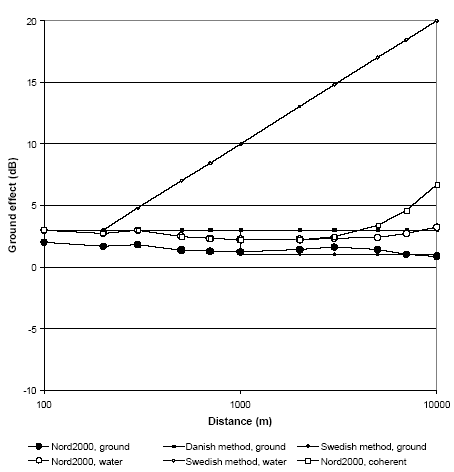
Figure 11 shows that for propagation over ground both the Danish and Swedish method predict a ground effect of +3 dB up to 1000 m while the calculations with Nord2000 at a wind speed of 8 m/s are 1 or 2 dB lower. At distances above 1000 m the Swedish method is 2 dB lower than the Danish method and thus shows good agreement with Nord2000. Figure 11 shows for propagation over water good agreement between Nord2000 and the Danish method, although Nord2000 has a slightly increasing tendency above 1000 m, however without the differences becoming pronounced. If coherent summation is used in Nord2000, a somewhat larger increase of ground effect and therefore of the sound pressure level due to multiple reflections is seen, and at large distances a good agreement is seen with the measurements at low frequencies in [4]. Nord2000 shows, however, that the distance must be larger than 1000 m even at coherent summation in the whole frequency range before the multiple reflections become of any importance. Viewed in the light of the calculations and the results in [8] it seems unrealistic that this effect occurs below 1000 m as indicated in the Swedish method. In addition calculations have been made of the ground effect of the sound propagating from a wind turbine with a hub height of 100 m, which corresponds to the size of wind turbines relevant today (Modern MW-turbines is approx. 80-90 m). Figure 12 shows the results of the calculations for this turbine height. Figure 12 Ground effect for a wind turbine with a hub height of 100 m calculated according to different models at propagation both over ground and water.
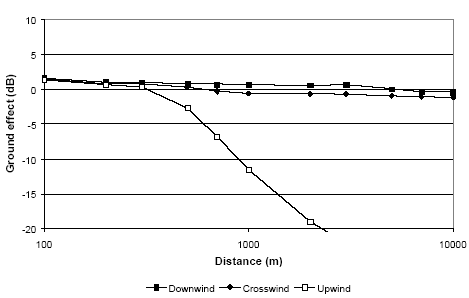
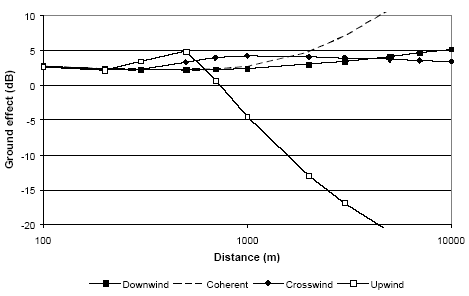
Figure 12 shows that the ground effect calculated with Nord2000 for a wind speed of 8 m/s is slightly higher than for the 30 m wind turbine, by which the difference between the Danish method and Nord2000 is correspondingly reduced. It should be particularly noted in the figure that the effect of multiple reflections does not occur until at very large distances (above 4000 m). For these high wind turbines it must be concluded that the Danish method regarding ground effect yields good results for a wind speed of 8 m/s, and that multiple reflections are without importance in the area of distance which is of practical importance. The Danish and Swedish method is only valid for sound propagation in downwind. To illustrate the effect of the meteorological conditions in crosswind and upwind, calculations were made with Nord2000 of the ground effect of sound propagating both over ground and water for a wind speed of 8 m/s for the three wind directions (downwind, crosswind, upwind). The results of the calculations are shown in Figure 13 to Figure 16. Figure 13 Ground effect for a wind turbine with a hub height of 30 m calculated with Nord2000 for different wind directions for propagation over ground.
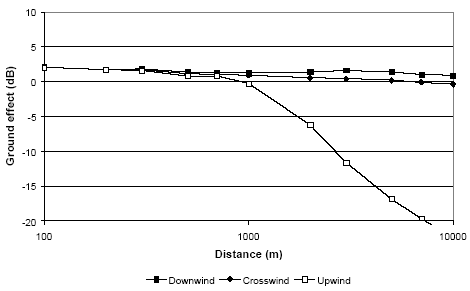
Figure 14 Ground effect for a wind turbine with a hub height of 30 m calculated with Nord2000 for different wind directions for propagation over water.
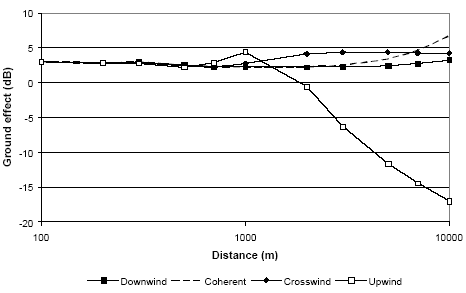
Figure 15 Ground effect for a wind turbine with a hub height of 100 m calculated with Nord2000 for different wind directions for propagation over ground.
Figure 16 Ground effect for a wind turbine with a hub height of 100 m calculated with Nord2000 for different wind directions for propagation over water.
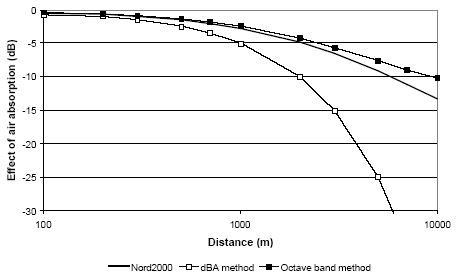
Figure 13 to Figure 16 show that the crosswind ground effect does not deviate much from the downwind ground effect. Actually, the figures show that the ground effect may be slightly higher (higher noise levels) during crosswind than during downwind at large distances. The reason is that the path length difference of the direct wave from source to receiver and the wave reflected from the ground is smaller in a neutral atmosphere than in a downward refracting atmosphere (meaning that the reflection from the ground is more likely to approach a +6 dB effect in the former case at large distances). The same effect can be seen during upwind conditions at distances just below the distance where a shadow zone appears. In upwind large attenuations can be observed above a given distance due to a meteorological shadow zone. Below this distance the ground effect will by and large correspond to the situation for the other wind directions. As far as high wind turbines are concerned shadow zones will only occur at considerable distances (above 1000 m) both for propagation over ground and water. Meteorological effects may also arise due to temperature gradients, but as this will only be of importance at low wind speeds, where the wind turbine noise is of less importance, these effects may be neglected for wind turbines. 3.4 Air AbsorptionIn addition to the ground effect the air absorption will affect the calculated The best method for calculating air absorption is ISO 9613-1 [11]. This method is used in Nord2000 [9] and is here supplemented with a principle for the difference between the air absorption in a 1/3-octave band and at the centre frequency, which may be of importance at propagation over very large distances. Use of the method requires that the sound power level of the source is known in 1/3-octave bands, which is normally the case. The approximate methods of both the Danish and the Swedish model (the dBA as well as the octave band methods) can be sufficiently accurate at small distances, but can give considerable errors at large distances as shown in Figure 17. The figure shows less than 1 dB difference between Nord2000 and the Danish dB(A)-method up to 500 m, but at 2000 m the difference is approx. 5 dB and at 10 km more than 35 dB. The agreement between Nord2000 and the Danish octave band method is considerably better as the difference for the wind turbine investigated is less than 0,5 dB up to 1000 m, less than 1 dB up to 3000 m, and approx. 3 dB at 10 km distance. The octave band method may be brought in better agreement with Nord2000 by adjusting the attenuation coefficients and introducing attenuation coefficients for frequency bands below 250 Hz. Figure 17 Effect of air absorption for a wind turbine with a hub height of 100 m calculated with Nord2000 for 15°C and 70% RH compared to calculation according to the Danish dB(A)-method.
As mentioned earlier the approximate methods for determining the air absorption will be sufficiently accurate at small distances. The ISO 9613-1 method as described in Nord2000 [9] is, however, so relatively simple that from a technical point of view there is no reason for not taking advantage of the extra accuracy of the method for a given source spectrum and possible given temperature and air humidity. 3.5 ConclusionCalculations with Nord2000 and a source spectrum of a modern 2MW wind turbine show that for a downwind of 8 m/s and for distances up to 1000 m the ground effect on sound propagating over water will give a little higher sound pressure levels (approx. 1 dB) than when sound is propagating over ground. As Nord2000 gives 1 or 2 dB lower ground effect than the existing Danish dB(A)-method, this means that the Danish method has approx. the same ground effect as Nord2000 for propagation over water. For propagation over water at a downwind of 8 m/s at distances above 1000 m effects of multiple reflections may occur (sometimes called sound channelling or cylindrical propagation) which are not seen for sound propagating over ground. This may result in sound pressure levels of 15-20 dB over free field at large distances and low frequencies. The calculations of this report as well as other results from the literature indicate that the effect of multiple reflections begin at distances of 1 or 2 km for low wind turbines (hub height 30 m) and not until above approx. 5 km for high wind turbines (hub height 100 m). A Swedish method stating a possible effect from multiple reflections already at distances from 200 m does not seem realistic. Calculations of the ground effect in crosswind show limited change compared to the ground effect in downwind. In upwind large attenuations can be observed above a given distance due to meteorological shadow zones. Below this distance the ground effect will on the whole be similar to the situation for other wind directions. As to high wind turbines shadow zones will not occur until at considerable distances (above 1000 m) regarding propagation over ground as well as over water. The approximate methods of the existing Danish model calculating the effect of air absorption seem to give reasonable results at small distances, but may give considerable errors at larger distances. Calculations show less than 1 dB difference between Nord2000 and the dB(A)-method up to 500 m, but at 2000 m the difference is approx. 5 dB and at 10 km above 35 dB. The difference between the Nord2000 calculations and the octave band method is considerably smaller. The ISO 9613-1 method as described in Nord2000 is relatively simple so from a technical point of view there is no reason for not taking advantage of the extra accuracy of the method. For a standardized meteorological situation (temperature and relative air humidity) the Nord2000 method will merely become a 1/3-octave band method with constant attenuation coefficients in each frequency band. It is, however, assessed also to be possible to make the octave band method in better agreement with Nord2000 by adjusting the attenuation coefficients and in particular introducing attenuation coefficients for frequency bands below 250 Hz.
|