Planteoptag af miljøfremmede, organiske stoffer fra slam
6. Modelberegninger
6.1 Modeller
6.1.1 Transportbeskrivelser
6.1.2 Fordeling mellem vand og plantedele
6.1.3 Samlede modelbeskrivelser
6.2 Input til modellerne og indledende beregninger
6.2.1 Forsøgsresultaterne
6.2.2 Beregning af porevandskoncentrationen
6.2.3 Interpolation af data
6.2.4 Stofdata
6.2.5 Indledende beregninger, baseret på massebalanceestimater
6.3 Modelberegninger
6.3.1 Beregningsresultater fra en-kompartment model
6.3.2 Beregningsresultater fra PlantX
6.3.3 Beregningsresultater fra Paterson & Mackays model
Formålet med de gennemførte modelberegninger af planteoptaget af DEHP og LAS er en validering af eksisterende planteoptagsmodeller; dvs. at undersøge, hvorledes resultaterne af beregninger med allerede eksisterende modeller afspejler de målinger af planteoptaget i byg og gulerødder, der er foretaget i projektet.
6.1 Modeller
Der er udviklet adskillige modeller til beskrivelse af planters optag af organiske stoffer. Modellerne befinder sig på forskellige detaljeringsniveauer:
Modelniveauer
- simple screeningskorrelationer; f.eks. Travis & Arms (1988)
- generiske (generelle) modeller, f.eks. 1-kompartment modellen af Trapp & Matthies (1995), som er foreslået anvendt i EUs Technical Guidance Document (TGD) (EU, 1996) i forbindelse med vurderinger af det humane indtag af organiske stoffer via føde. Denne model er en simplifikation af en mere kompliceret model (PlantX). Kun koncentrationen i bladene estimeres ved modellen. Derudover estimerer EUs TGD koncentrationen i rødderne ud fra en antagelse om ligevægt mellem stoffet i jordens porevand og stof bundet i rødderne.
- mere komplekse og dynamiske modeller som f.eks. modellen af Paterson et al. (1994), PlantX af Trapp (1995) og Hung & Mackay (1998).
I nærværende fokuseres der på følgende tre modeller: En-kompartment modellen af Trapp & Matthies (1995), den mere komplicerede PlantX (Trapp, 1995) samt Paterson et al’s model (1994).
Opdeling af planten
Alle modeller betragter systemet jord-planter-luft. Planten videreopdeles typisk i delene: frugt, stængel, rødder og blade. Hver plantedel består så igen af en vandfase og en "fastfase" samt en luftfase. Nogle af modellerne betrager alene lipiddelen i den "faste" fase, mens en kulhydratfase inddrages i andre modeller.
Én-kompartment-modellen beregner udelukkende koncentrationen i plantens blade, mens de to andre modeller beregner koncentrationer for hver af plantedelene (kompartments): Blade, stængler, frugter og rødder; for de sidste baseret på både optag i plantens ledningsvæv og diffusion ind i rødderne og med efterfølgende fordeling i planterøddernes faser.
Fordeling i plantedelenes faser
Stofferne vil søge at blive fordelt mellem de forskellige faser, så der opnås ligevægt i systemet. Denne ligevægt kan beskrives enten ud fra fordelingskoefficienter eller ud fra det termodynamiske isofugacitetsbegreb, der siger, at ved ligevægt er fugaciteten af et stof den samme i alle faser. I princippet dækker isofugacietesbegrebet og ligevægtsfordelingsbegrebet dog over det samme.
Transporten af stoffer mellem de forskellige plantedele vil foregå som en advektiv og/eller en diffusiv transport.
Modelelementer
I alle tre modeller indgår beskrivelser af:
- Transportprocesser, hvis hastighed bl.a. styres af, hvor langt systemet er fra
ligevægt. Disse transportprocesser kan foregå på mindst to måder:
- diffusion
- advektion
- Ligevægtsfordelingen af stoffet mellem de forskellige faser
- Nedbrydning af stoffet i jorden
- Nedbrydning af stoffet i planten
- Fortynding ved vækst
6.1.1 Transportbeskrivelser
Diffusion
Diffusionen i én fase styres af koncentrationsgradienter i et medie. Diffusionen mellem to faser styres af, hvor langt koncentrationen i faserne er fra de koncentrationer, der ville gælde ved ligevægt.
Advektiv transport
Den advektive transport af et stof kan beskrives som en passiv transport af stoffet i et medie (her vand), hvor den samlede advektive stoftransport beskrives ud fra (her) vandflowet (Q) og stofkoncentrationen (C): Den advektive transporthastighed af stoffet = Q×C. Et godt eksempel på advektiv transport her er stoffernes transport med strømmen i xylemet og i phloemet.
Optag med med transpirationsvandet
Sættes optaget af vand fra rødder til QT og koncentrationen i porevandet til CPW, er mængden af stof optaget gennem rødderne:
(1)
NT = QT× CPW
Som tidligere omtalt, er den kaspariske stribe og cellemembranerne ved endodermis semipermeable, og kun en brøkel (Transpiration Stream Concentration Factor, TSCF) af stofferne passerer disse.
Denne brøkdel, kan eventuelt beregnes af (Briggs et al., 1982):
(2)
Dette udtryk er fundet at passe godt for optag af ikke-ioniserede, organiske stoffer i adskillige plantearter. Udtrykket indgår i EUs TGD (EU, 1996) i forbindelse med risikovurdering af kemiske stoffers optag i planter f.eks. fra slam-behandlede jorde.
Passage af endodermis
Mængden af stof, der passerer endodermis og når ind plantens indre del, udtrykkes således ved:
(3)
NT(endodermis) = QT× CPW× TSCF
Den brøkdel, der ikke passerer endodermis, bliver tilbage i den ydre del af roden, nedbrydes eventuelt dér eller diffunderer tilbage til jordmiljøet igen.
6.1.2 Fordeling mellem vand og plantedele
De fleste modeller opdeler de enkelte plantedele (rødder, stængler, blade og frugter) yderligere i i følgende faser
Tabel 6.1
| Fase | Bestanddele i planten |
| Luft | intercellular luft |
| Vand | mellemrum mellem cellevægge cytoplasma vakuoler xylem phloem |
| Polær del (en stor del af det organiske indhold i cytoplasma og vakuoler) | polysaccharider uorganiske salte proteiner |
| Lipider | membran-lipider olier depot-lipider resiner |
Beregning af fordelings-koefficienter
Fordelingen af stofferne i de enkelte plantedele er afhængig af størrelsen af de enkelte faser og stoffets karakter. Et meget hydrofobt stof vil således have en tendens til at blive koncentreret i lipidfasen, mens de mere polære stoffer vil have en større tendens til at blive akkumuleret i vandet og den polære del af plantematerialet.
Ligevægtsfordelingen mellem stoffer i jordens porevand og i en plantedel (X) er generelt beskrevet ved (Trapp, 1995):
(4)
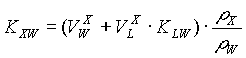
hvor:
| er fordelingskoefficienten til beskrivelse af stoffets fordeling mellem plantedelen og den eksterne opløsning | |
| er lipid-vand –fordelingskoefficienten for stoffet | |
| er vandindholdet i plantedelen [masse/masse vådvægt] | |
| er lipid-indholdet i plantedelen [masse/masse vådvægt] | |
| pW | er densiteten af vandfasen |
| pX | er densiteten af plantedelen X |
:Et lidt udvidet udtryk (Hung & Mackay, 1998) i forhold til det tidligere nævnte tager også hensyn til kulhydrat- og luftfasen:
(5)

hvor:
Kcw er kulhydrat-vand -fordelingskoefficienten for stoffet
![]() er luft-vand -fordelingskoefficienten for stoffet
er luft-vand -fordelingskoefficienten for stoffet
![]() er luftindholdet i plantedelen [masse/masse vådvægt]
er luftindholdet i plantedelen [masse/masse vådvægt]
![]() er kulhydrat-indholdet i plantedelen [masse/masse
vådvægt]
er kulhydrat-indholdet i plantedelen [masse/masse
vådvægt]
Følgende udtryk er fundet til beregning af de forskellige fordelingskoefficienter:
(6)
![]() (Hung & Mackay, 1998)
(Hung & Mackay, 1998)
(7)
![]() (Trapp, 1995)
(Trapp, 1995)
(8)
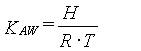
hvor:
b er en empirisk faktor, som typisk er tæt på 1
H er Henrys konstant
R er gaskonstanten (8,314 Pa•m3/(mol•K))
T er den absolutte temperatur (K)
6.1.3 Samlede modelbeskrivelser
I tabel 6.2 er der givet et overblik over de processer, de enkelte modeller har medtaget. For en nærmere beskrivelse henvises til symbollisten.
VKI har modtaget programmer for PlantX-modellen (i FORTRAN) modellen af Paterson og Mackay (i Basic). Begge modeller er blevet omprogrammeret til Pascal. Verifikation af de omprogrammerede modeller er foregået ved at sammenligne på et par eksempler og sikre, at de samme beregningsresultater er opnået.
Tabel 6.2 Processer medtaget i de anvendte modeller
Tabel: Se her
6.2 Input til modellerne og indledende beregninger
I det følgende redegøres der kort for de antagelser, der ligger til grund for beregningerne, udover de antagelser, der er grundlag for de forskellige modeller.
6.2.1 Forsøgsresultaterne
Som beskrevet i kapitel 5 er der generelt ikke fundet et indhold af LAS i planterne, der kan relateres til indholdet i jord/slamblandingerne, og de målte koncentrationer er alle meget lave og nær detektionsgrænsen. Den eneste undtagelse herfra er en højere koncentration af LAS i bygrødder ved de højeste slamkoncentrationer. Denne kan dog muligvis tilskrives medtagelse af slamrester i prøverne trods omhyggelig afrensning.
Noget tilsvarende gør sig gældende for DEHP indholdet i både rødder og overjordiske plantedele, omend de målte koncentrationer i gulerodstop og rødder er væsentligt over detektionsgrænsen. Koncentrationen af DEHP er højest i gulerodsskræl, men den er ikke relateret til koncentrationen i jord/slamblandingerne, omend der er en vis sammenhæng mellem koncentrationen i skræl og i de tilsvarende prøver af gulerodskerne. Det kan dog ikke udelukkes, at de målte mængder af DEHP i gulerodsskræl (og evt. kerne) stammer fra partikler, der enten har været (relativt ukontamineret) jord eller (kontamineret) slam.
I blade og stængler af byg lå DEHP-indholdet lige over detektionsgrænsen i prøver fra alle slam/jordblandinger, mens indholdet i gulerodstop lå højere og værdierne var meget svingende uden nogen korrelation til DEHP-koncentrationen i jorden. Det anses derfor for sandsynligt, at det fundne DEHP stammer fra atmosfærisk optag snarere end fra jorden.
Resultaternes karakter (usikkerheden om, hvorvidt de målte koncentrationer i rodprøver stammer fra jord/slampartikler) vanskeliggør anvendelse af dem til modelvalidering. Dog giver de gennemførte beregninger mulighed for at belyse hvilke forhold, der er af betydning for resultaterne af de enkelte modeller, og for LAS resultaternes vedkommende er det muligt at drage konklusioner baseret på forsøgsresultaterne.
Med henblik på belysning af hvilke forhold, der har betydning for udfaldet af modelberegningerne, tages der i diskussionen mindre hensyn til resultaternes karakter, ligesom der snarere fokuseres på størrelsesordenen af måle- og beregningsresultaterne end på enkeltværdierne.
6.2.2 Beregning af porevandskoncentrationen
Til beregning af stoffernes koncentration i jordens porevand, antages det simpelt, at der er ligevægt mellem bundet stof, og stof opløst i jordens porevand. Herved er følgende massebalance opstillet:
(9)
![]()
hvor:
| CTotal | er den totale stofkoncentration (opløst + bundet stof) [masse/masse tørvægt] |
| CPW | er porevandskoncentrationen [masse/rumfang] |
| STOT | er den samlede mængde fast materiale [masse tørvægt] = SSLAM+ SJORD |
| SSLAM | er den samlede mængde slam [masse tørvægt] |
| SJORD | er den samlede mængde jord [masse tørvægt |
| W | er den samlede mængde vand [rumfang] |
| KD,TOT | er vand-jord ligevægtsfordelingskoefficienten, som beregnes
som et vægtet gennemsnit af ligevægtsfordelingskoefficienten for slam h.h.v.
jord[rumfang/masse tørvægt]:
|
| fSLAM | er brøkdelen af slam i forhold til den samlede mængde fast materiale i forsøgsskålen [tørvægt] |
| fJORD | er brøkdelen af jord i forhold til den samlede mængde fast materiale i forsøgsskålen [tørvægt] |
| KD,Slam | er slam-vand ligevægtsfordelingskoefficienten for stoffet [rumfang/masse tørvægt] |
| KD,Jord | er jord-vand ligevægtsfordelingskoefficienten for stoffet [rumfang/masse tørvægt] |
6.2.3 Interpolation af data
Stofkoncentrationer i jord/slam blanding
Stofkoncentrationerne i jord/slam blandingen kendes kun ved opsætning og ved afslutning af forsøgene. Til interpolation mellem de to tider, er det antaget, at alle fjernelsesprocesser (nedbrydning, planteoptag) er førsteordens reaktioner med hensyn til koncentrationen (dvs. nedbrydningshastigheden er proportional med stofkoncentrationen) og med samme hastighedskonstant gennem forsøget:
(11)
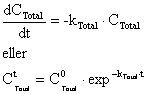
(12)
hvor:
![]() er en første ordens hastighedskonstant for fjernelse af
stof [dag-1]
er en første ordens hastighedskonstant for fjernelse af
stof [dag-1]
![]() er den totale stofkoncentration til tiden = t
[masse/masse tørstof]
er den totale stofkoncentration til tiden = t
[masse/masse tørstof]
![]() er den totale stofkoncentration til tiden = 0
[masse/masse tørstof]
er den totale stofkoncentration til tiden = 0
[masse/masse tørstof]
Denne udvikling i stofkoncentrationen af stof i jorden gennem forsøgsperioden er anvendt i modelberegningerne, bortset fra Paterson & Mackay-modellen, der er baseret på halveringstider af stofferne i jord.
Temperatur og luftfugtighed
Temperaturen har primært betydning for fordampningshastigheden af stofferne. Temperaturen i forsøgene har varieret mellem 10°C og 25°C. Der er gennemført en følsomhedsanalyse af betydningen af temperaturen på beregningsresultaterne, og det er fundet, at variationen på de beregnede koncentrationer i planten er på under 1% ved variation af temperaturen mellem 10°C og 25°C. Det skal dog hertil bemærkes, at Henrys konstant i disse beregninger var holdt konstant.
Den relative luftfugtighed har primært betyding for stofudvekslingen med luften. Den har varieret mellem 10% og op til ca. 40% i forsøgene. Der er ligeledes gennemført en følsomhedsanalyse af betydningen af den relative luftfugtighed på beregningsresultaterne, og det er fundet, at variationen på de beregnede koncentrationer i planten er på under 6%(0% for LAS) ved variation af den relative luftfugtighed på mellem 10% og 40%.
I beregningerne er temperaturen efterfølgende sat til 16°C og den relative luftfugtighed til 37% (byg). For beregningerne med gulerødder er temperaturen sat til 20°C og den relative luftfugtighed til 33%
Plantedata
Transpirationshastigheden er antaget at være konstant i hele perioden, hvilket ikke aktuelt vil være tilfældet. Dette vil give en forholdsvis forhøjet bestemmelse af stoffets optag i planten, da den højeste transpirationshastighed givet er ved slutningen af forsøgene, hvor bladarealet er størst. I slutningen af forsøgene er stofkoncentrationen i jorden samtidig lavere end ved opsætning, bl.a. pga. nedbrydning i jorden.
Data til karakterisering af planterne (bladareal, bladvolumen, bladmasse, plantemasse etc.) findes ved lineær interpolation mellem forholdene ved opsætning af forsøg og ved afslutning af forsøg. Sammensætningen i plantedelen primært m.h.t. vandindhold og lipidindhold er antaget konstant igennem forsøgene.
I det oprindelige udtryk i den simple en-kompartment model (Trapp og Matthies, 1995) blev en eksponentiel vækst af bladvolumen antaget:
(13)
![]()
hvor:
lG er en vækstfaktor
Da dette udtryk kræver kendskab til bladvolumen til minimum to forskellige tidspunkter, er det ikke velegnet til simulering af de udførte forsøg. I stedet er, som tidligere nævnt, anvendt en lineær interpolation mellem bladvoluminet ved start af og ved afslutning af forsøgene.
6.2.4 Stofdata
DEHP og LAS må betragtes som fysisk-kemisk meget forskellige stoffer.
DEHP
DEHP er et hydrofobt stof (logKOW = 7,5) (Pedersen & Larsen, 1996)1 med en vandopløselighed på ca. 0,05 mg/l. Med en Henry’s konstant H » 3•10-7 atm m3/mol (Pedersen & Larsen, 1996) forventes stoffet at kunne fordampe i et vist omfang, hvorfor der kan være et vist indhold af DEHP i luften. En repræsentativ koncentration af DEHP i luften angives til ca. 1,0×10-8 g/m3 af Riederer (1995). Danske værdier for indholdet af DEHP i luften2 kan beregnes til ca. 4,4×10-9 g/m3.
Nedbrydning
Fotolyse forventes ikke at være en væsentlig nedbrydningsproces for DEHP. DEHP kan nedbrydes mikrobielt under aerobe betingelser. Mineralisering af DEHP er målt til 75 - 93 % ved en inkubationstid på 140 dage i koncentrationer mellem 2 og 20 ppm i tre forskellige jorder tilsat slam (Pedersen & Larsen, 1996). I en blanding af slam og Jyndevad jord (15oC, 28 dage, slamkoncentration = 15 g/kg jord) er fjernelsen af DEHP målt til ca. 9% ved kemisk analyse (Madsen et al., 1998). Jorden var altså den samme, og slammet var endvidere fra samme anlæg, som det, der er anvendt i dette projekt. DEHP er, som tidligere nævnt, påvist at blive metaboliseret i planter.
Fordelingskoefficient
LogKOC (KOC er fordelingskoefficienten for forholdet mellem stofkoncentrationen i den organiske kulstoffase og stofkoncentrationen i vand) er ved studier af DEHP’s binding til jord fundet at være på ca. 5, hvilket svarer godt til den logKOC = 5,2, der kan beregnes v.hj.a. QSAR-programmet EPIWIN (Syracuse, 1996). DEHP’s fordelingskoefficient i en slamberiget (1 del slam til 58 dele jord - på tørbasis) jord fra Foulum blev målt til mellem 6900 l/kg (2 dage efter sammenblanding af slam og jord) og 12400 l/kg (7 dage efter sammenblanding af slam og jord) (Henriksen et al. 1998). Det organiske indhold i Foulumjord er på ca. 2,6%, hvilket svarer til et organisk kulstofindhold på ca. 1,45%. Det organiske kulstofindhold i det anvendte slam var på 28,5%. Ved antagelse om at DEHP primært bindes til jordens organiske materiale, og ved at benytte ovennævnte måledata for KD i slamgødet jord beregnes en logKOC mellem 5,6 og 5,8. KD for DEHP i Jyndevadjord forventes at være på ca. KD = KOC×fOC =(105,6 - 105,8 ) 0,013 [l/kg] = 5100 - 9200 [l/kg]. Den højeste værdi benyttes i beregningerne. DEHP’s binding til slammet beregnes tilsvarende til ca. (105,6 - 105,8 ) 0,25 [l/kg]3 = 100.000 - 160.000 [l/kg]. Den højeste værdi benyttes i beregningerne.
TSCF
TSCF, som er af betydning for den videre transport af stoffet ind i planten,forventes at kunne beregnes ud fra Briggs’ udtryk (ligning (2)).
LAS
LAS, der er et anionisk tensid, vil kunne befinde sig i vandfasen i høje koncentrationer. Ved de lave koncentrationer (under CMC) er stoffet i reel opløsning, mens LAS ved de højere koncentrationer danner miceller. Det har en meget lav flygtighed fra vand, hvorfor luftens indhold af LAS forventes at være negligibelt. Dog indeholder støv i indeluft betydelige mængder LAS (Vejrup 1996). LAS er endvidere ioniserbart, hvorfor det må forventes at befinde sig både på ioniseret (anionisk) og på neutral form.
Nedbrydning
LAS er letnedbrydeligt under aerobe betingelser men nedbrydes ikke under anaerobe forhold. En halveringstid på ca. 26 dage er fundet for LAS i en slam-jord matrix (15oC, 28 dage, slamkoncentration = 15 g/kg jord) (Madsen et al., 1998). LAS forventes at blive omsat i planter i et vist omfang.
Binding til slam
Bindingen af LAS til slam er i litteraturen fundet at variere mellem ca. 1000 l/kg og 5200 l/kg. Bindingen er bl.a. afhængig af slamtypen (aktivieret slam, primær slam etc) og kædelængden. Her antages en binding af LAS til slam på 1900 l/kg TS, hvilket er angivet som en gennemsnitlig KD for LAS til slam (Painter, 1992).
Binding til jord
Bindingen af LAS til jord er meget afhængig af kædelængden af LAS og af jordtypen. LAS er således fundet at blive bundet til visse lerfraktioner (f.eks kaolinite) samt kraftigt til humus (se f.eks. Matthijs & De Henau, 1985). Fordelingskoefficienten for LAS i humussyre er fundet til ca. 1000 - 1700 [l/kg], hvoraf en logKOC på 2,8 - 3,0 kan beregnes. Bindingen er endvidere pH-afhængig. I bilag 5 er målinger af fordelingskoefficienten for LAS i forskellige jordtyper samlet. Ved sammenligning af data gengivet i bilag 5 med textur-data for Jyndevadjorden, vurderes det, at KD for LAS i Jyndevadjord er på ca. 4 [l/kg].Det skal dog bemærkes, at der i øjeblikket ikke foreligger data, der muliggør en præcis fastlæggelse af KD for et et ladet overfladeaktivt stof som LAS.
TSCF
TSCF for LAS er ikke umiddelbart nem at bestemme. Dette skyldes dels, at det kan optræde både som anion og neutralt, dels dets tenside egenskaber. TSCF forventes at være meget lav, da LAS sandsynligvis primært vil befinde sig på anionisk form. I modelberegningerne anvendes derfor to værdier for TSCF; dels beregnes den efter Briggs’ udtryk (ligning (2)), dels beregnes den TSCF-værdi, der passer bedst til resultaterne af dyrkningsforsøgene.
De egenskaber for stofferne LAS og DEHP, der er anvendt i modelberegningerne, er opsummeret i tabel 6.3.
Tabel 6.3
Stofdata
| Egenskab | DEHP | LAS |
| Mw [g/mol] | 391 |
298 (C10)- 340 (C13). Gnm. molvægt ved opsætning er på ca. 325 |
| Vandopløselighed [mg/l] | 0,05 | blandbar med vand |
| H [atm× m3/mol] | 3 × 10-7 | - |
| LogKOW | 7,5 (målt) | 3,7 |
| LogKOC [l/kg] | 5,6 – 5,8 (målt) | 2,8 – 3,0. |
| KD,jord [l/kg] | 5100 – 9200 | 4 |
| KD,slam [l/kg] | 100.000 – 160.000 | 1900 |
| Nedbrydning i jord |
I jord: 9% væk på 28 dage (målt) | Halveringstid i jord » 26 dage (målt) |
| Koncentration i luft |
4,4× 10-9 g/m3 | Antaget lig med nul. |
| TSCF | Antages at kunne følge Briggs udtryk (ligning(2)) | Antages ikke at kunne følge Briggs udtryk |
6.2.5 Indledende beregninger, baseret på massebalanceestimater
Der er udført nogle indledende massebalancebetragtninger for LAS og DEHP for de udførte forsøg. Disse illustrerer svaghederne ved anvendelse af modeller, baseret på simple forudsætninger.
Der er anvendt to beregninger, der begge ser bort fra nedbrydning af stofferne i planterne :
1. Forskellen i den mængde stof, der er forsvundet fra jorden, fra jord med planter hhv. fra jord uden planter, er antaget som et mål for den mængde stof, der er optaget i planten. En maksimal gennemsnitskoncentration i hele planten kan herved beregnes.
2. mængden af stof, der er optaget i planten er lig med transpirationen af planterne ganget med koncentrationen i porevandet gennem vækstperioden (ligning (11)). Den brøkdel, der maksimalt kan være i planten er fundet ved at gange denne optag med TSCF for stofferne, beregnet efter Briggs (ligning (2)). Koncentrationen i blade + stængel, henholdsvis hele planten, er beregnet ud fra den målte tørvægt ved høst.
Resultaterne er samlet i bilag 7, og skal kort kommenteres her.
Beregningsmetode 1
Ved beregning af planteoptaget med metode 1 beregnes en koncentration i planten, der er meget højere end de målte koncentrationer i planten. Dette gør sig gældende for alle forsøg og begge stoffer. For LAS beregnes op til flere tusinde mg/kg TS, for DEHP op til ca. 100 mg/kg TS.
- Nedbrydning af stoffer i planten kan forklare noget af denne forskel.
- Derudover er det sandsynligt, at tilstedeværelsen af planter fremmer nedbrydning af stofferne i jorden, dels ved at fremme ilttransporten ned i jorden, og dels ved at sikre, at de nødvendige mikroorganismer har gode betingelser for vækst. Dette bevirker, at en del af koncentrationsforskellene i forsøg med plantedække hhv. uden plantedække, kan skyldes en øget nedbrydning i jorden, når der er planter til stede.
- Endvidere kan fjernelsen af stofferne lige omkring planterødderne ved planteoptag og nedbrydning bevirke, at der er lavere koncentrationer lige omkring plantens rødder end i det øvrige jordsystem. Dette vil give en lavere koncentration i porevandet og dermed et reelt lavere planteoptag end det, der estimeres ud fra gennemsnitsberegninger.
Beregningsmetode 2
Beregningerne efter metode 2 giver forskellige resultater for LAS og DEHP.
LAS-koncentrationerne i planten beregnet ved metode 2 er (som ved metode 1) væsentligt højere end de målte koncentrationer, som alle er under detektionsgrænsen. Forskellige mulige forklaringer på disse forhold kan nævnes:
- Metabolisering af LAS i planten, hvilket bevirker et koncentrationsfald i planten. Det er dog ikke muligt at godtgøre, hvor stor en del af forklaringen, dette udgør.
- Anvendelsen af Briggs’ udtryk til beregning af TSCF har overestimeret denne, hvis kun en meget lille del af LAS kan passere endodermis. For at opnå overensstemmelse mellem måleresultater og beregninger skal TSCF-værdien for LAS være under ca. 0,00035.
- At - jævnfør tidligere forklaring - fjernelsen af LAS lige omkring planterødderne ved planteoptag og nedbrydning bevirker, at der er lavere koncentrationer her end i det øvrige jordsystem.
- At nedbrydningshastigheden af LAS omkring slampartiklerne er sammenlignelig med eller større end den transporthastighed, hvormed LAS diffunderer igennem porevandet. Herved vil den LAS-mængde, der reelt er tilgængelig for planteoptag blive mindre, end når en gennemsnitlig koncentration i hele jordmatrix anvendes.
De med metode 2 beregnede DEHP-koncentrationer i planterne er lavere end de målte koncentrationer - undtagen ved den højeste slamdosering. Betragtes modelberegningernes forudsætninger isoleret, kan mulige forklaringer på dette forhold være:
- At de beregnede porevandskoncentrationer er for lave, dvs. der er benyttet for høje KD-værdier for DEHP i jord.
- At bindingen af DEHP til og i roden er meget væsentlig, og beregningerne derfor ikke udelukkende kan baseres på stof, der optages i plantens ledningsvæv (TSCF).
- At den TSCF-faktor, som beregnes for DEHP ved hjælp af Briggs korrelation er for lav. Benyttes de her fundne måledata for DEHP i gulerødderne (kerne + skræl), kan en TSCF-faktor for DEHP i gulerødderne estimeres til 0,1-0,3 (se bilag 6), hvilket indikerer væsentligt højere passage igennem endodermis, end det, som beregnes ved anvendelse af Briggs’ korrelation. De antagelser, der er gjort for estimeringen af TSCF er dog meget grove, hvorfor det ikke kan anbefales at bruge disse værdier. Da de koncentrationer, der er målt i skræl og kerne af gulerødderne, ikke er relateret til koncentrationen af DEHP i jorden, er disse betragtninger endvidere relativt teoretiske.
- At DEHP-indholdet i planternes overjordiske dele stammer fra luften.
6.3 Modelberegninger
Med henblik på sammenligning af resultaterne af de tre forskellige modeller og de målte koncentrationer i planterne er disse samlet i figur 6.1 - 6.4, der hver især viser koncentrationerne af et stof i enten rødder eller blade + stængel. Resultaterne er endvidere vist i tabelform i bilag 8-10.
Figur 6.1
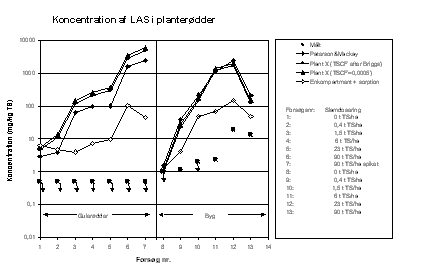
Sammenligning af resultaterne af de tre modeller og eksperimentelle data. Koncentration af LAS i planterødder.
Figur 6.2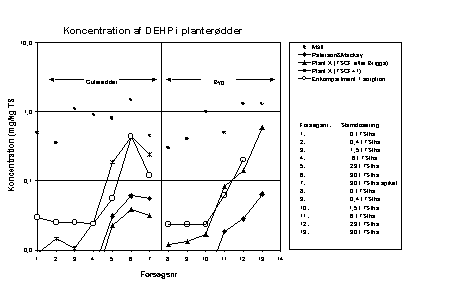
Sammenligning af resultaterne af de tre modeller og eksperimentelle data. Koncentrationer af DEHP i planterødder.
Figur 6.3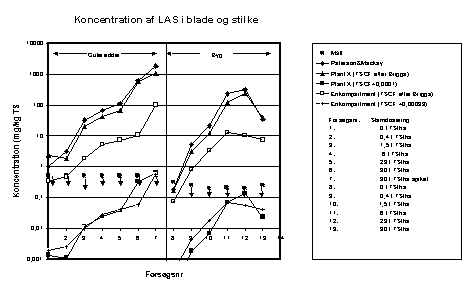
Sammenligning af resultaterne af de tre modeller og eksperimentelle data. Koncentrationer af LAS i blade og stængler.
Figur 6.4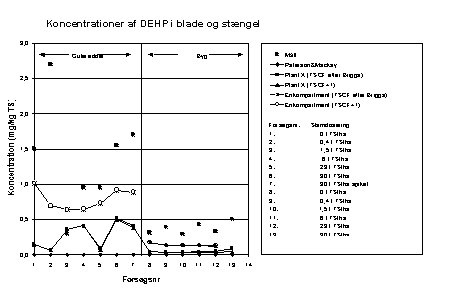
Sammenligning af resultaterne af de tre modeller og eksperimentelle data. Koncentrationer af DEHP i blade og stængler.
6.3.1 Beregningsresultater fra en-kompartment model
Den samme massebalance, som er opstillet af Trapp og Matthies (1995), er anvendt. Massebalancen er, i modsætning til Trapps og Matthies (1995), løst numerisk. I beregningerne er der set bort fra nedbrydningen af stofferne i planterne.
De beregnede koncentrationer ved anvendelse af den simple en-kompartment model er suppleret med de beregnede stofkoncentrationer i rødderne efter den metode, der anvendes i TGD (EU, 1996). Sidstnævnte er baseret på antagelse af en simpel ligevægtsfordeling mellem opløst stof og stof bundet i rødderne. Resultaterne er samlet i bilag 8 og illustreret i figur 6.1-6.4.
Det simple ligevægtsfordelingsprincip overestimerer LAS-koncentrationen i rødderne (figur 6.1). Dette gælder for begge planter. Dette kan skyldes, at der reelt ikke er opnået ligevægt mellem stof i jordsystemet og stof i planternes rødder, pga. langsom transport (ved diffusion) af stofferne fra jordsystemet til rødderne. Det kan delvist også skyldes, at den anvendte fordelingskoefficient for LAS i slam-jordsystem er for lav. Der er en vis tillid til, at den anvendte fordelingskoefficient for LAS i jord har den rigtige størrelsesorden. Endvidere kan, som omtalt ovenfor, planteoptag og nedbrydning ved slampartikler bevirke en heterogen fordeling af stofferne i jordmatricen - med lave koncentrationer i umiddelbar nærhed af rødderne til følge.
Det simple ligevægtsfordelingsprincip underestimerer DEHP-koncentrationen i rødderne. (6.2). Dette gælder for begge planter. Den anvendte fordelingskoefficient for DEHP i jordsystemet er muligvis for høj.
For LAS overestimeres koncentrationen både i rødderne og i planten som helhed (figur 6.1 og 6.3). Dette svarer til de resultater, der blev opnået ved de simple massebalancebetragtninger ovenfor, og forklaringerne er de samme. Det er beregnet, at TSCF-faktoren for LAS skal være i størrelsesordenen < 0,00033 (Briggs udtryk beregner en TSCF for LAS på 0,17) for at opnå bedre overensstemmelse mellem målte og beregnede koncentrationer i blade + stængel, hvilket er illustreret på figur 6.3.
Det fremgår af figur 6.4, at de beregnede DEHP-koncentra-tioner i bladene er på niveau med de målte koncentrationer, og af bilag 8, at stort set al den DEHP, der efter beregningerne er i bladene på både gulerod og byg, stammer fra luften. I beregningerne er anvendt den baggrundskoncentration af DEHP i atmosfærisk luft, der er omtalt i afsnit 6.4.3.
6.3.2 Beregningsresultater fra PlantX
De beregnede koncentrationer, ved anvendelse af PlantX-modellen kan ses i bilag 9. I beregningerne er der set bort fra nedbrydningen af stofferne i planterne.
Der er i lighed med beregningerne ovenfor anvendt TSCF-værdier efter Briggs og for LAS endvidere estimeret en mere "realistisk" TCSF-værdi: 0,0005.
Det fremgår af figur 6.1-6.4 at
DEHP-koncentrationen i rødderne af både byg og gulerod (figur 6.2) bliver under-estimeret ved modelberegningen, undtagen ved den højeste slamdosering for gulerod. De beregnede koncentrationer i rødderne er ca. en faktor 10 lavere end de målte koncentrationer.
Koncentrationen af DEHP i blade + stængel (figur 6.4) bliver ligeledes underestimeret med en faktor på ca. 10. Koncentrationen i blade + stængel er kun meget lidt afhængig af koncentrationen i jorden og af TSCF-faktoren, hvorfor luftens indhold af DEHP kan antages at udgøre den største kilde til DEHP i bladene.
For LAS er den beregnede koncentration i rødderne og i blade + stængel væsentligt højere end de målte koncentrationer som ved beregningerne ovenfor, og forklaringerne er de samme. Ved anvendelse af en TSCF-faktor for LAS på < 0,0005 (Briggs udtryk beregner en TSCF for LAS på 0,17) opnås bedre overensstemmelse mellem måleresultater og beregninger.
6.3.3 Beregningsresultater fra Paterson & Mackays model
Resultaterne af beregningerne med Paterson & Mackay-modellen kan ses i bilag 10. I beregningerne er der set bort fra nedbrydningen af stofferne i planterne. Nedbrydningshastigheden i jorden for de to stoffer er sat til de værdier, der er angivet i tabel 17.
Af figur 6.1-6.4 fremgår det, at resultaterne af beregninger med denne model er stort set sammenfaldende med resultaterne af PlantX-modellen, når TSCF beregnes efter Briggs’ udtryk. Dette er ikke overraskende, da de to modeller er baseret på de samme grundlæggende principper for beregning af opkoncentrering af stof i planter og ligevægtsfordeling af stoffer mellem forskellige faser.
I Paterson & Mackay-modellen beregnes stofkoncentrationen i jorden gennem forsøgsperioden ud fra koncentrationen ved forsøgsstart og en (målt eller beregnet) halveringstid for stoffet i jord. For DEHP og LAS er der anvendt målte halveringstider, og sådanne målinger gennemføres altid uden planter i forsøgsopstillingen.
I figur 6.5 er de slut-koncentrationer i jorden, der er estimeret med Paterson & Mackay-modellen, afbildet sammen med de målte koncentrationer ved afslutning af forsøgene i kar med og uden planter. I figuren er der ikke skelnet mellem resultater af målinger og beregninger på de to stoffer. Bemærk den dobbelt-logartimiske afbildning.
Figur 6.5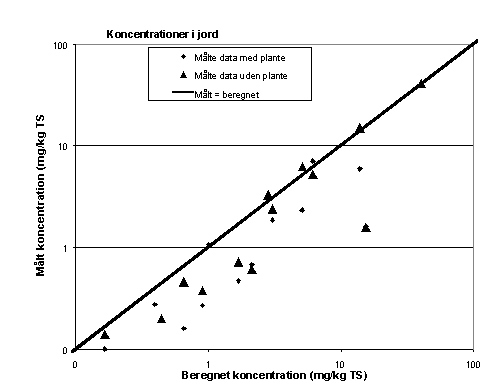
Sammenligning af beregnede og målte stofkoncentrationer (LAS og DEHP) i jorden ved forsøgenes afslutning.
Af figur 6.5 fremgår det, at resultaterne af modelberegningerne og de målte koncentrationer er af samme størrelsesorden. Dog ligger langt de fleste af de målte koncentrationer i kar med og uden planter under de beregnede (diagonalen). Der er en tendens til, at data fra kar uden planter er nærmere de beregnede koncentrationer, specielt for de højere koncentrationer. Ved de lavere koncentrationer ligger alle måledata under de beregnede. Ved simulering med lavere nedbrydningshastighed kan der dog opnås en bedre overensstemmelse mellem målte og beregnede stofkoncentrationer i jord: for LAS giver en halveringstid på ca. 15 dage og for DEHP en halveringstid på ca. 50 dage således den bedste overensstemmelse. Dette tyder på, at den stimulering af nedbrydningen, der er påvist i kar med planter (afsnit 6.4.5), kan afspejles af modelberegningerne.
1. Der er meget stor usikkerhed på DEHP’s fysisk-kemiske egenskaber. Her benyttes de fysisk-kemiske egenskaber for DEHP, som, på basis af en kritisk gennemgang af eksisterende data for stoffet, er anbefalet af Pedersen & Larsen (1996) 2. Nedfaldet af DEHP med nedbør af målt til ca. 0,2 mg/m2/år (Vikelsøe, 1998), hvilket med en antagelse om en årlig nedbør på 700 mm giver et indhold i regnvand på 0,33 mg/m3. Med en Henrys konstant på 3× 10-7 atm× m3/mol og en molvægt på 390,6 g/mol svarer dette til et indhold i luften på ca. 4,4× 10-9 g/m3 3. Slammets indhold af organisk kulstof er ikke målt, men det forventes at være omkring 0,25 kg/kg TS