Følgevirkninger af råstofgravning under grundvandspejlet, Miljøstyrelsen

Følgevirkninger af råstofgravning under grundvandspejlet

Indholdsfortegnelse

Sammenfatning og konklusioner (Sammenfattende artikel)

Summary and conclusion (Summary)

2. Indledning

3. Løsninger fra litteraturen
3.1 Varmeledning i faste stoffer
3.2 Grundvandsstrømninger

4. Grundvandssænkning som følge af vådgravning
4.1 Opstilling af ligninger
4.2 Analytisk løsning
4.2.1 Vandspejlet i råstofgraven
4.2.2 Vandspejlet i grundvandsmagasinet
4.2.3 Praktisk eksempel
4.3 Vådgravningens påvirkning af vandbalancen
4.4 Diskussion af resultater
4.5 Oversigt over formler og fremgangsmåde

5. Referencer

Bilag A Matematisk løsning af vådgravningsproblemet

Forord

Udarbejdelsen af denne vejledning blev igangsat efter oplæg fra KANmiljø og startet i november 1999. Arbejdet er udført i samarbejde mellem KANmiljø og Instituttet for Geologi og Geoteknik samt Instituttet for Bygningsfysik, Chalmers Tekniske Universitet, Göteborg.

Miljøstyrelsens styregruppe har bestået af Martin Skriver og Bente Villumsen. Styregruppens arbejde er afsluttet i marts 2000.

Arbejdet er nært forbundet med tidligere projekter vedrørende vandindvinding og råstofgravning, som har været udført under Miljøstyrelsen i samarbejde med Skov- og Naturstyrelsen.

Sammenfatning og konklusioner

Råstofgravning under grundvandsspejlet giver anledning til grundvandssænkninger i den opståede råstofsø og i grundvandsmagasinet omkring graven. Det har været sædvane at ligestille råstofgravningen med en oppumpning af grundvand og anvende kendte metoder fra prøvepumpningspraksis til at beregne sænkninger hidrørende fra gravningen. Analogien til pumpning er imidlertid ikke fysisk korrekt, idet en pumpning fjerner vand fra graven, mens en råstofgravning flytter vand fra grundvandsmagasinet ind i graven på grund af den opståede ændring af magasintallet i graven fra den aktuelle effektive porøsitet til eksakt 1. Det må forventes, at de virkelige sænkninger derfor bliver mindre end de, der beregnes på den nævnte måde. Dette er også den erfaring, der er gjort ved konkrete råstofgrave, hvor der vådgraves efter grus.

For at udvikle en metode til at beregne konsekvenserne af en vådgravning er de matematiske ligninger, der definerer problemet, opstillet og løst analytisk. Løsningen er testet mod et konkret eksempel fra Skåne og viser god overensstemmelse med observerede data. De resulterende formler involverer de matematiske funktioner som kendes fra prøvepumpningsteorien og er derfor relativt enkle at anvende i praksis. Den konkrete løsning er foretaget i det radiære tilfælde, idet det har vist sig at være praktisk uigennemførligt med andre geometrier. Imidlertid er det radiære tilfælde også det mest anvendelige, idet den fundne løsning med god tilnærmelse kan anvendes på alle råstofgrave, der har polygonform med nogenlunde ens kantlængder.

Løsningen viser det overraskende resultat, at sænkningen i selve graven er uafhængig af tiden. I gravningens første fase etableres en momentan sænkning af grundvandsspejlet, og denne sænkning øges ikke med tiden. Udvidelsen af graven resulterer altså i en indstrømning af grundvand til graven, som balancerer eksakt det råstofvolumen, som fjernes. I selve grundvandsmagasinet vil sænkningerne vokse med tiden, men de vil naturligvis være begrænsede af, at sænkningerne i sø og grundvandsmagasin er ens ved gravefronten.

De opstillede formler til beregning af sænkninger i grav og grundvandsmagasin forudsætter konstant gravning. I praksis vil der være ophold i graveprocessen, og der vil ske en retablering af grundvandsspejlet. Den opståede råstofsø vil derfor optræde som en buffer og have en stærkt dæmpende effekt på sænkningerne. Dette formodes at være en væsentligt medvirkende årsag til, at der ikke synes at være observeret egentlige sænkninger i og omkring råstofgrave efter længere tids gravning. Den udviklede metode til beregning af sænkninger som en konsekvens af råstofgravning kan derfor anvendes til at beregne de maksimale sænkninger, som gravningen vil forårsage, og disse må således formodes at indtræde i den tidlige fase af gravningen.

Som en konsekvens heraf anbefales, at gravningen generelt indledes med at etablere et så stort søareal som muligt, og at gravningen foregår langsomt i starten. Det tilrådes endvidere, at konsekvenserne af gravningen dokumenteres i form af en nøje registrering af de opgravede råstofmængder på f.eks. daglig eller ugentlig basis, og at der foretages en løbende måling af grundvandsspejlet i og omkring råstofgraven. Disse målinger bør suppleres med daglige målinger af nedbøren.

Summary and conclusions

Mining alluvial deposits below the groundwater table causes drawdowns to occur in the pit and around the quarry. When calculating drawdowns in the aquifer resulting from the mining activities it has been customary to use the theories from water well testing by considering the mining process as one of groundwater pumping. However, this analogy is not physically correct since pumping removes water from the pit, whereas quarrying moves groundwater from the aquifer to the pit as a result of changing the porosity from the actual value to exactly 1. It should be expected, that actual drawdowns in the aquifer will be smaller than the ones calculated in the way mentioned. This is also the experience gained in actual cases of mining below the water table.

In order to develop a method which more accurately describes the actual process, the mathematical equations governing the groundwater flow have been written down and solved analytically. The solution has been tested against actual data from a gravel pit in Skåne and shows very good agreement. The formulas derived involve mathematical functions well known from well testing theories and should therefore be relatively simple to use in practical applications. Det solution presented has been developed in cylindrical coordinates, since it proved to be unpractical to apply any other geometry. Cylindrical coordinates are, however, the most practical geometry, since the circular pit is an acceptable approximation to most polygon shaped quarries with edges having approximately the same lengths.

The mathematical solution shows the surprising result, that the drawdown in the pit is time independent. During the first stage of quarrying an abrupt water table drawdown is established and this drawdown does not increase with time. As the circumference of the pit expands, the volume of groundwater flowing into the pit balances the volume of aquifer material excavated in such a way, that the drawdown is constant. In the aquifer proper drawdowns will increase with time, but these drawdowns are limited since at the pit-aquifer interface drawdowns are equal at all times.

The formulas derived for calculation of drawdowns assume a constant rate of excavation. In reality there will interruptions and during such periods the water level will recover partly or in full. The pit, therefore, will act as a buffer and reduce drawdowns. This is believed to be the main reason, that no substantial drawdowns seem to have been observed in and around quarries after longer periods of excavation. The formulas, therefore, can be used to calculate the maximum drawdowns as a result of quarrying below the groundwater table, and such drawdowns must be expected to exist during the early phases of quarrying only.

As a consequence of this, it is recommended that quarrying is initiated by establishing as large a pit area as possible, and that the excavation rate is slow at the beginning. Further, it is recommended, that the consequences of excavation are documented through continuous monitoring of groundwater levels in the pit and in the aquifer, and keeping records of aquifer material excavated on a daily or weekly basis. Finally, rainfall should be recorded on a daily basis.

2. Indledning

Udvinding af råstoffer under grundvandsspejlet giver anledning til grundvandssænkninger i takt med udvindingen. I forbindelse med udstedelse af gravetilladelser synes der ikke i Danmark at have været en etableret praksis for, hvilke forhåndskrav der stilles til sænkningernes størrelse og dermed påvirkningen af omkringliggende brønde og boringer. Det har været anvendt ved vurderingen af følgevirkningerne af vådgravning at ligestille bortgravning af råstof med oppumpning af en tilsvarende mængde grundvand og anvende velkendte metoder til beregning af sænkningerne omkring en boring, se f.eks. Miljøministeriet (1980 og 1992).

Denne analogi er imidlertid kun en tilnærmelse til den fysisk korrekte virkelighed. Ved en oppumpning fjernes vandet helt fra grundvandsmagasinet og dette giver således anledning til en konkret reduktion af magasinindholdet. Under en vådgravning fjernes ikke vand men råstof fra grundvandsmagasinet, og den fjernede mængde råstof erstattes i råstofgraven af en tilsvarende mængde indstrømmende grundvand. Der er altså tale om en omrokering af vandmængderne under gravning, og set ud fra et overordnet vandbalancesynspunkt er der ikke sket nogen ændring i områdets vandbalance, idet der ses bort fra de ændrede nedbørs- og fordampningsforhold og den vandmængde, der hænger ved det opgravede råstof, og som ikke ledes tilbage til graven.

I praksis svarer en vådgravning derfor blot til en ændring af magasintallet (eller mere præcist den effektive porøsitet) fra den aktuelle værdi på typisk 0,1 - 0,2 for grus, til eksakt 1 inde i graven.

Det er den fremherskende opfattelse blandt såvel tilsynsmyndigheder som entreprenører, som beskæftiger sig med råstofindvinding under grundvandsspejlet, at de resulterende sænkninger er små. I forbindelse med dette projekt er der ikke fundet sager, hvor en vådgravning har givet anledning til klager over følgevirkningerne af de frembragte sænkninger. Dette kan være en væsentlig årsag til, at der ikke tidligere er foretaget beregninger af, hvilke sænkninger der konkret frembringes under vådgravningsprocessen.

3. Løsninger fra litteraturen

3.1 Varmeledning i faste stoffer

Matematisk beskrives grundvandsstrømninger ved hjælp af de samme ligninger som beskriver varmeledning i faste stoffer, og en række velkendte løsninger på grundvandsstrømninger er da også hentet fra varmelæren ved at udnytte analogien. Når en råstofgravning opfattes som en ændring af magasintallet inde i graven, er analogien til varmeledning en ændring af materialets tilstand, f.eks. størkning eller smeltning. Herved ændres både den termiske ledningsevne og varmekapaciteten af materialet, svarende til, at der i det tilsvarende grundvandsproblem sker en ændring af den hydrauliske ledningsevne og magasintallet i råstofgraven. Disse fysiske ændringer sker på den ene side af en bevægelig front, der adskiller de to tilstandsformer, og der foregår en strømning af varme, henholdsvis grundvand, over denne front som følge af de fysiske ændringer.

Problemstillingen med en bevægelig front har i varmelæren været undersøgt så tidligt som i 1891 af Stefan, som opstillede ligninger til bestemmelse af polarisens tykkelse. Carslaw og Jaeger (1959) angiver løsninger i en del tilfælde. Disse er mere komplicerede end det tilsvarende grundvandsproblem, fordi der foregår varmestrømning på begge sider af skillefladen, hvilket ikke er tilfældet i grundvandsproblemet, hvor der i graven ikke er nogen hydraulisk gradient og derfor ingen strømning. Det, at skillefladen bevæger sig, frembyder særlige problemer, som gør det matematiske problem ikke-lineært, hvilket betyder at antallet af foreliggende analytiske løsninger er begrænsede. Kreith og Romie (1955) viste, at en analytisk løsning normalt kun kan findes, hvis temperaturgradienten over skillefladen er konstant i tid og sted.

I tilfældet med lineær strømning, altså strømning i kun én retning, findes flere løsninger, som dog ikke er relevante, fordi der stilles krav til begyndelsesbetingelser, som ikke er realistiske i en grundvandssammenhæng. F.eks. giver Carslaw og Jaeger (1959), p .292 en eksakt løsning til et tilfælde med en front, der bevæger sig med konstant hastighed. For at få fjernet den nævnte ikke-linearitet kræves, at begyndelsestemperaturen ved x = 0 er negativ og vokser eksponentielt med tiden., hvilket gør løsningen uanvendelig i alle praktiske sammenhænge. Samme sted, p. 295, angives en løsning i det radiære tilfælde, hvor skillefladen bevæger sig med , hvor t er tiden. Samtidig foregår der en varmeproduktion (der pumpes), og begyndelsesbetingelserne kræver et eksisterende cylindrisk område (en eksisterende grav) med en temperaturforskel over skillefladen, hvilket ikke finder sted i grundvandsproblemet.

I varmelæren beskrives eksempler på varmeledning i et fast stof der har modstandsfri kontakt til en perfekt varmeleder med foreskreven temperatur, altså et legeme med samme temperatur overalt til enhver tid. Dette svarer netop til strømningen omkring en råstofgrav, idet råstofgraven har samme vandspejlsniveau overalt. Carslaw og Jaeger (1959), p.342, giver løsningen til temperaturfordelingen i et uendeligt område begrænset internt af en cylindrisk perfekt leder med konstant varmeproduktion. Denne løsning er anvendt af Papadopoulos og Cooper (1967) til at beregne sænkningerne i en boring med stor diameter, hvorfra der pumpes med konstant kapacitet.

Et tilsvarende og velkendt problem i lineær strømning er et halvuendeligt medium med foreskrevet overfladetemperatur gennem kontakt med en perfekt varmeleder. Jacob (1950) benyttede analogien til grundvandsstrømninger til at bestemme hydrauliske parametre for et grundvandsmagasin med kontakt til havet, og hvor vandstanden svinger i takt med tidevandsfluktuationen.

Imidlertid har alle kendte løsninger, som involverer en perfekt varmeleder, fast rand, og derfor er der ingen af disse løsninger, der umiddelbart kan anvendes til at beskrive det aktuelle grundvandsproblem.

3.2 Grundvandsstrømninger

Løsninger til grundvandsproblemer skal findes primært i litteratur vedrørende minedrift. En stor del af denne litteratur er rettet mod en beskrivelse af de geokemiske ændringer, som minedriften forårsager. De strømningstekniske løsninger knytter sig væsentligst til oppumpning af grundvand fra mineskakter eller råstofsøer, og især forholdene efter endt minedrift er beskrevet. Der er derfor typisk tale om løsninger med fastholdt geometri. Et eksempel kan findes i Koch (1986), hvor der angives semi-empiriske løsninger til råstofgravning, som kontrolleres ved en sammenligning med Theis løsninger for sænkningerne omkring en boring. Løsningerne er ikke anvendelige i denne sammenhæng, fordi der regnes med fast rand, og råstofgravningen ækvivaleres med pumpning af grundvand. Aral og Sturm (1982) foretog en 3D finite element analyse af at pumpe fra en lavvandet sø i rotationssymmetri, men igen anvendes fast geometri. Lignende arbejde er publiceret af Hamilton og Wilson (1977), men med hovedvægt på de regionale strømningsforhold omkring graven. Ingen af de nævnte publikationer præsenterer egentlige feltdata.

Landberg (1982) udfører ligeledes modelarbejder til undersøgelse af strømningen omkring grusgrave og præsenterer sænkningsdata fra et konkret graveprojekt.

4. Grundvandssænkning som følge af vådgravning

4.1 Opstilling af ligninger

Problemet, der skal løses, er vist skematisk på Figur 4.1. Det er valgt at løse ligningerne i rotationssymmetri, idet dette dels giver væsentlige matematiske fordele, men tillige er en cirkulær grav en passende praktisk tilnærmelse til en grav, som har horisontal tilstrømning fra alle sider, og hvis sider har nogenlunde samme længde. Tilnærmelsen vil altså være dårligere, jo mere langstrakt graven er. Grundvandsmagasinet har uendelig horisontal udstrækning og befinder sig i området 0 <<H, hvor H er den vandmættede højde inden gravningen starter. Grundvandsmagasinet regnes homogent og isotropt med hydraulisk ledningsevne K_h. Transmissiviteten er T=K_h·H. Den effektive porøsitet er é, 0< é<1. Der ses bort fra den vandmængde, der fjernes fra søen sammen med det opgravede materiale. Gravningen starter til tiden =0 og foregår på en sådan måde, at der graves en konstant råstofmængde pr. tidsenhed, og der graves over hele højden H. Arealet af søen i graven vil derfor vokse

lineært med tiden og radius r_f(t) af søen med

Sænkningen af søens vandspejl h_f (t) er lig med sænkningen h(r,t) i grundvandsmagasinet ved skillefladen.

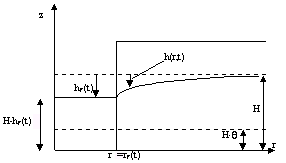
Figur 4.1

Skematisk illustration af vådgravning.

Strømningsproblemet beskrives ved hjælp af en styrende differentialligning med tilhørende begyndelses- og randbetingelser. For en detaljeret beskrivelse af ligninger og løsning henvises til Bilag A.

Differentialligningen lyder

(4.1)

hvor

(m²/s) er diffusiviteten.

Her er benyttet tilnærmelsen

Begyndelses- og randbetingelse er

(4.2)

Sænkningen i søen og i grundvandsmagasinet skal være ens ved skillefladen:

(4.3)

Dette gøres ved hjælp af en global vandbalance

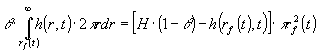(4.4)

I ligning (4.4) udtrykker venstre side den vandmængde, der er fjernet fra grundvandsmagasinet, mens højre side er et udtryk for det nettovolumen, der er fjernet fra graven, se nærmere beskrivelse i Bilag A.

For at ligningerne skal kunne løses, er det nødvendigt at specificere gravebetingelserne og dermed r_f (t). Det antages, at det udgravede volumen er konstant pr. tidsenhed, og at gravningen starter ved r = 0. Dette resulterer i ( se Bilag A)

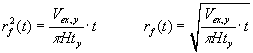(4.5)

Her er

(m³) det udgravede volumen inden for en given tidsperiode

(for eksempel 1 år).

er således gravehastigheden.

Det udgravede volumen vokser lineært med tiden, hvilket betyder, at

bliver proportional med kvadratroden af tiden.

Introduceres den dimensionsløse konstant:

(4.6)

fås ved at kombinere (4.5) og (4.6):

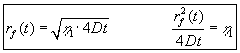(4.7)

Parameteren

er kvadratet på forholdet

Nævneren

er et mål for det område i grundvandsmagasinet,

inden for hvilket der sker sænkninger til tiden t under graveprocessen. Dette udtryk er velkendt fra teorien fra grundvandsstrømninger omkring en boring. ^{En lille
værdi af} ^{betyder, at det påvirkede område er stort i forhold til} ^{radius af det} udgravede område.

Ligningssystemet til bestemmelse af er nu:

(4.8)

(4.9)

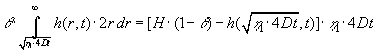(4.10)

4.2 Analytisk løsning

Løsninger til (4.8) er ofte en funktion af parameteren

Der søges derfor en løsning af formen

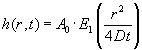(4.11)

Her er det det såkaldte eksponentielle integral

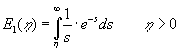(4.12)

Fra teorien om pumpning fra boringer er det eksponentielle integral også kendt som "boringsfunktionen", der indgår i Theis’ formel. Løsningen ses let

at opfylde (4.8) – (4.9). Faktoren

skal bestemmes ved

indsættelse i (4.10). Efter en del regning som er beskrevet i Bilag A findes

(4.13)

Den endelige løsning findes ved at indsætte (4.13) i (4.11),

		(4.14)

Her er indført en ny funktion, som passende kan benævnes et modificeret eksponentielt integral:

(4.15)

Funktionens graf er vist i Bilag A.

4.2.1 Vandspejlet i råstofgraven

Sænkningen,

af vandspejlet i råstofgraven findes ved indsættelse

af (4.3) og (4.7) i (4.14):

(4.16)

Der fremkommer det overraskende resultat, at sænkningen er uafhængig af tiden. Det betyder, at gravningen bevirker en momentan sænkning af vandspejlet i graven, og herefter holder sænkningen sig konstant.

Den første faktor i løsningen

er den maksimalesænkning,

der kan opnås, og den opstår ved, at der ikke strømmer vand ind i graven

under graveprocessen. Det svarer til, at vandhøjden i graven er

(4.16) kan simplificeres ved at rækkeudvikle det eksponentielle integral og kun beholde betydende led. Dette er vist i Bilag A. Resultatet er:

Equation Section (Next)

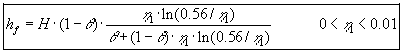(4.17)

Fejlen, der begås ved at benytte denne formel er mindre end 1% i det angivne interval og mindre end 5% for .

4.2.2 Vandspejlet i grundvandsmagasinet

Sænkningen i grundvandsmagasinet, afhænger af r og t på en relativ enkel måde. Af (4.14) fås:

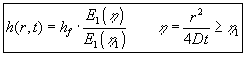(4.18)

Sænkningen i selve graven , er givet af (4.16) eller approximationen (4.17). Værdien af h er lig med for . I grundvandsmagasinet varierer h som .

Figure 4.2 viser grafen for og funktionens asymptoter for for små og store værdier af . For små og store har funktionen følgende asymptoter (Abramovitz og Stegun, 1964):

(4.19)

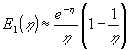(4.20)

Tallet 0.577 er Eulers konstant (		Fejlen ved at benytte
approximationen		(4.19)

er mindre end 1% for

mindre end 0.002% for

og lig to 9% for		De to første led,
vil normalt være tilstrækkelige for

Den ret grove approximation

(4.20)

tilnærmer

for store argumenter. Den relative fejl er mindre end 12%

for

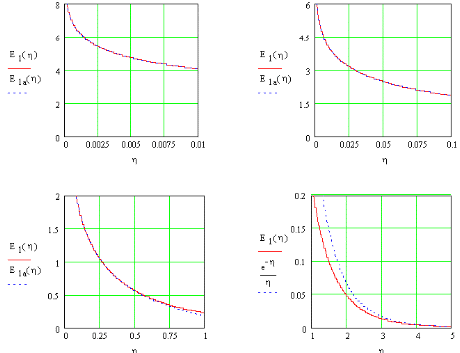
Figur 4.2.

Det eksponentielle integral
(4.12),

og dets asymptoter
(4.19- .20).

4.2.3 Praktisk eksempel

Landberg (1982) præsenterer data fra starten af grusgravning ved Örsjö i det sydvestlige Skåne. Der er gravet i tre perioder med måling af vandspejlsændringer i en boring, som er placeret i kanten af søen. Om boringen har en egentlig afstand til søen, og hvad den i givet fald er, vides ikke. Vandspejlsændringerne som funktion af gravning og nedbørshændelser er vist i Figur 5.3.

Det ses, at der er en hurtig respons på nedbøren, men også at gravningen giver omgående respons. Der er gravet i tre adskilte perioder, og gravningen giver tilsyneladende anledning til størst sænkninger i den første periode, hvor der ikke er en eksisterende råstofsø, som kan dæmpe sænkningerne. Tages højde for den trend, der er årstidsbetinget, forårsager gravningen sænkninger i søen af størrelsen 0,03-0,08 m. Der er en god indikation af, specielt i graveperiode 2, at sænkningen optræder momentant, og at den er konstant i tiden.

Der er udført prøvepumpning i grusgraven til bestemmelse af hydrauliske parametre, og der er foretaget opgørelser over opgravede grusmængder. Til kontrol af de udledte formler anvendes data fra graveperiode 1, som havde en varighed på 32 dage. Den gennemsnitligt opgravede mængde anvendes ved gravning 24 timer pr. døgn. Landberg (1992) angiver således følgende data:

= 27 m., = 0,18, = 0,0007 m/s, = 5440 m³ på 32 dage,

= 0,019 m²/s, = 0,106 m²/s.

Af (4.6) fås

Figur 4.3.

Grundvandsspejl og nedbør ved Örsjö 1972 –10- 01 – 1974-12-31, (Landberg,1982).

Da kan de tilnærmede udtryk anvendes. Af
(4.15)

fås

og vandspejlssænkningen i søen bestemmes af approksimationen
(4.17)

m.,

hvilket ligger i det observerede interval.

I Bilag A er foretaget en gennemregning af formeludtrykkene i et tænkt tilfælde og sammenlignet med de sænkninger, der forekommer ved pumpning. Det viser sig ikke overraskende, at sænkningen i grundvandsmagasinet er større, når gravningen opfattes som pumpning af grundvand. I bilaget er vist,

at for små værdier af kan sænkningerne i grundvandsmagasinet ved

gravning bestemmes ved at beregne sænkningen som ved pumpning fra en

boring og dernæst multiplicere resultatet med . For små porøsiteter

giver gravning af en volumenenhed grundvandsmagasin, (hvor vandet løber tilbage i graven) og pumpning af en volumenenhed grundvand altså næsten samme resultat, mens store porøsiteter giver markant større sænkning ved pumpning. I praksis vil sænkningen ved gravning som regel altid være små, hvilket hænger sammen med den måde, der graves på, se afsnit 4.4.

4.3 Vådgravningens påvirkning af vandbalancen

Når overjorden fjernes og grundvandet blotlægges som en sø, sker der en ændring af grundvandsbalancen omkring råstofgraven. Opstrøms vil grundvandet normalt strømme ind i graven, mens der nedstrøms kan opstå en kildeskråning, især efter gravningens ophør eller under ophold i graveaktiviteterne. Under gravning kan der dog være tilstrømning til graven langs alle sider, afhængig af gravehastigheden. Men det er vigtigt at notere, at der ikke fjernes vand; det flyttes fra et nærområde omkring graven ind i selve graven, hvorfra det løber tilbage til grundvandszonen.

Under nedbørshændelser infiltreres søen direkte og vil derfor modtage mere vand end det omgivende grundvandsmagasin, og vand vil strømme ud af graven. Når nedbøren når grundvandsspejlet, vil grundvandet stige højere end inde i søen på grund af porøsiteten i grundvandsmagasinet, og grundvand løber tilbage til søen. Til gengæld mister søen vand på grund af fordampning. Denne fordampning afhænger af atmosfæriske forhold som vind, temperatur, luftfugtighed m.v., samt vandspejlsdybden i forhold til det omgivende terræn.

Landberg (1982) gennemgår eksempler på fordampning fra grusgravssøer i det nordlige Tyskland og i Sverige under klimatiske forhold, der er sammenlignelige med de danske. Det generelle indtryk er, at den årlige fordampning er 10-15% mindre end nedbøren. Den nettoinfiltration, som søen unddrages fordi dæklagene mangler, skal holdes op imod denne vandmængde, således at vådgravning ikke kan siges at udgøre en væsentlig belastning af grundvandsressourcerne. Som nævnt i indledningen er dette en opfattelse, som deles af hydrogeologer i amterne og af entreprenører, som driver råstofgrave, hvor der indvindes materiale ved gravning under grundvandsspejlet, uden at der iøvrigt foregår nogen grundvandsoppumpning. Diskussionen omkring en råstofsøs vandbalance er gennemgået mere detaljeret i Miljøministeriet (1992), hvortil henvises.

4.4 Diskussion af resultater

De opstillede formler for sænkningen i en råstofgrav og grundvandsmagasinet omkring graven er relativt simple, og elementerne i dem er velkendte fra prøvepumpning af boringer. Formlerne er udledt under de sædvanlige forudsætninger om homogenitet og isotropi, konstant gravehastighed, grundvandsmagasin af uendelig udstrækning o.s.v. Det er endvidere en forudsætning, at gravningen foregår til bunds af grundvandsmagasinet, således at det er hele grundvandsmagasinet, der fjernes. Gravningen foregår således, at graven udvider sig radiært og radius i graven vokser med kvadratroden af tiden.

Disse forudsætninger er naturligvis aldrig opfyldte på et konkret sted, men ligesom det er tilfældet ved tolkning af data fra prøvepumpninger, må det formodes at formeludtrykkene er en så tilpas tilnærmelse til virkeligheden, at de giver et virkelighedsnært billede af følgevirkningerne af en vådgravning, som det blev demonstreret ved eksemplet fra Örsjö ovenfor.

Formlerne forudsætter, at gravningen starter til tiden t=0 og fortsætter til aktiviteten endeligt ophører. Dette vil naturligvis medføre sænkninger som vokser med tiden i grundvandsmagasinet, mens sænkningen i graven er tidsuafhængig og således udgør den maksimale sænkning der kan opnås. Dette gør det muligt umiddelbart at anvende formlerne til at beregne sænkninger i forskellige afstande til forskellige tider. I praksis vil der altid være pauser i gravningen således, at vandspejlet får mulighed for at retablere sig. Når gravningen så starter igen, er der i graven opsamlet en buffer af vand, som dæmper sænkningernes størrelse. Jo større fri vandoverflade, jo større er denne buffer. Derfor vil det være en sund praksis at etablere en så stor sø som praktisk muligt i starten af gravningen for derved at mindske sænkningerne. Denne buffereffekt er en væsentlig årsag til, at der ikke observeres sænkninger i og omkring råstofgrave, hvor der vådgraves.

Før formlerne kan anvendes, skal der udføres en prøvepumpning til bestemmelse af hydraulisk ledningsevne og porøsitet. Dette foregår efter helt velkendte principper. Det anbefales, at der opstilles et pejleprogram omfattende råstofsø og boringer i nærheden af graven til dokumentation både af forudsigelser og de aktuelle følgevirkninger. Endvidere bør der holdes regnskab med det opgravede volumen på daglig eller ugentlig basis og opsættes regnmåler til daglig opgørelse af nedbøren.

4.5 Oversigt over formler og fremgangsmåde

Ved beregning af sænkningen i råstofgraven benyttes følgende fremgangsmåde:

Ud fra de givne størrelser , og bestemmes først

diffusiviteten eller . Her er

grundvandsmagasinets vandmættede tykkelse, er porøsiteten,

er det opgravede volumen råstof over perioden , og

er den hydrauliske ledningsevne. Dernæst bestemmes af
(4.6)

, og af (4.15):

Her betegner det såkaldte eksponentielle integral, der også er

kendt som boringsfunktionen . I praksis kan benyttes

tilnærmelsen
(4.19):

–

For er de to første led en tilstrækkelig approksimation.

Sænkningen i råstofgraven bestemmes af (4.16):

, hvor

er bestemt ovenfor. Denne værdi af sænkningen i søen vil altid være

worst case. I de fleste praktisk forekommende tilfælde vil en tilnærmelse til

svarende til approximationen ovenfor være tilstrækkelig
(4.17):

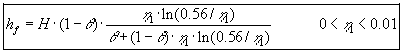Sænkningen i grundvandsmagasinet bestemmes af
(4.18):

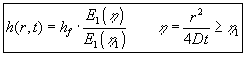er bestemt allerede og kan atter bestemmes ved hjælp af

approksimationen ovenfor.

Det ses af formlerne, at sænkningen i graven er tidsuafhængig, altså en konstant, som afhænger af gravekapacitet og fysiske parametre, mens sænkningen uden for graven er tidsafhængig. Figur 4.4 viser en skitse af dette.
Figur 4.4

Skitse af sænkninger under vådgravningsprocessen

5. Referencer

Abramowitz, M. and Stegun, I.A., 1964: Handbook of Mathematical Functions, Dover Publications, New York.

Aral, M.M. and Sturm, T.W., 1982: Ground Water Pumping from Axisymmetric Ponds. ASCE, Journal of the Hydraulics Division, Vol. HY 12, December.

Carslaw, H.S. and Jaeger, J.C.., 1959: Conduction of Heat in Solids. Oxford.

Hamilton, D.A. and Wilson, J.L., 1977: A Generic Study of Strip Mining Impacts on Groundwater Resources. Report No. 229, Massachusetts Institute of Technology.

Koch, D.,1986: Analytical Modeling of Groundwater Impacts by Mining. Ground Water Vol. 24 No. 2.

Kreith, F. and Romie, F.E., 1955: A study of the Thermal Diffusion Equation with Boundary Conditions corresponding to Solidification or Melting of Materials Initially at the Fusion Temperature. Proc. Phys. Soc. B, 68.

Landberg, J., 1982: Hydrogeological Consequences of Excavating Gravel Pits below the Water Table in Glaciofluvial Deposits, 1982: Publ.A 39, Chalmers University of Technology, Ph. D. Thesis.

Miljøministeriet,1980: Råstofindvinding og vandindvinding. Råstofkontorets arealdataserie nr.1.

Miljøministeriet, 1992: Projekt om konflikten mellem grusindvinding og vandindvinding. Fase 1.

Stefan, J., 1891: Ueber die Theorie der Eisbildung, insbesondere über die Eisbildung im Polarmeere. Ann. Phys. u. Chem. (Wiedemann) N.F.

Papadopulos, I.S. and Cooper, H.H., 1967: Drawdown in a Well of Large Diameter. Water Resources Research, Vol. 3, No. 1.

Bilag A: Matematisk løsning af vådgravningsproblemet

Det betragtede problem

Equation Section 1

Udvinding af sand, grus og andre råmaterialer under grundvandsspejlet giver anledning til sænkninger i den etablerede råstofsø og i grundvandsmagasinet omkring søen. Der søges en analytisk løsning på problemet med passende forudsætninger for derigennem at få en forståelse af processerne og bedømme den relative betydning af de ingående parametre.

Problemet er skitseret i Figur 1.1. Grundvandsmagasinet befinder sig i

området , er homogent og isotropt og har uendelig udstrækning.

Der anvendes rotationssymmetri, d.v.s der udgraves en cirkulær sø, således at sænkningen h (m) i forhold til begyndelsesniveauet afhænger af r og t.

Grundvandsmagasinets transmissivitet er , hvor er den

hydrauliske ledningsevne. Gravehastigheden antages at være konstant i tiden, hvilket betyder at arealet af den blotlagte sø vokser lineært med tiden.

Radius af søen vokser følgelig med kvadratroden af tiden.

Sænkningen i selve søen, er lig med sænkningen i

grundvandsmagasinet ved gravefronten. Grundvandsmagasinet har konstant

porøsitet Det antages, at alt grundvand forbliver i søen

under graveprocessen.

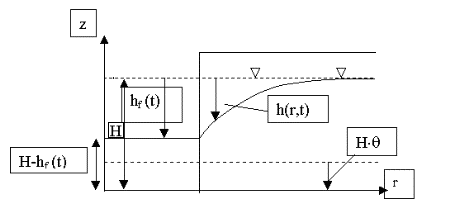
Figur 1.1.

Skematisk illustration af vådgravning.
Opstilling af strømningsligning

Den radiære grundvandsstrømning (m³/m²/s) er, idet det forudsættes, at sænkningerne er små, d.v.s

(1.1)

Kontinuitetsligningen svarende til afstanden r og tiden t lyder

(1.2)

Kombineres disse to ligninger fås strømningsligningen

(1.3)

Her betegnes (m²/s) diffusiviteten.
Global vandbalance

Sænkningen, i den cirkulære sø ,

og sænkningen i grundvandsmagasinet er ens ved gravefronten:

(1.4)

En global vandbalance bestemmer sænkningen :

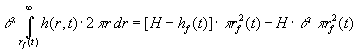(1.5)

Venstre side udtrykker den vandmængde, der er strømmet fra

grundvandsmagasinet ( ) ind i søen.

Det første led på højre hånd er vandvoluminet i søen ⁽⁾

til tiden t, og det andet led er det under gravningen frigivne vand. Det tidsafledte udtryk for (1.5) kunne også være anvendt, men den integrerede form giver væsentlige regnelettelser.

Ligninger for sænkningen

Begyndelsessænkningen og sænkningen langt fra graven er 0. Ligningerne for

er nu,
(1.3-5):

(1.6)

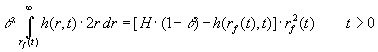Gravebetingelserne skal specificeres for at bestemme

En analytisk løsning kan kun findes under særlige vilkår.

Konstant gravehastighed

Det antages, at gravehastigheden er konstant, og at gravning starter ved

. Dette giver:

(1,7)

Her betegner (m³) det udgravede volumen gennem en periode

(for eksempel 1 år). Det udgravede volumen vokser lineært med tiden,

hvilket betyder at er proportional med kvadratroden af tiden:

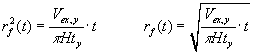(1.8)

Faktoren foran t giver en basisk dimensionsløs konstant :

(1.9)

Ved at kombinere (1.8) og (1.9) fås:

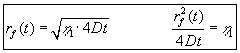(1.10)

Parameteren er kvadratet på forholdet .

Nævneren er et mål for det påvirkede område til tiden t i forhold

til kanten af søen. En lille værdi af er udtryk for, at radius af det påvirkede område er stort i forhold til søens radius.

bestemmes nu ved løsning af følgende ligninger:

(1.11)

(1.12)

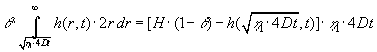(1.13)

Analytisk løsning

Der søges en løsning på formen

Equation Section (Next)

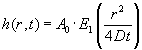(1.14)

Her betegner det såkaldte eksponentielle integral:

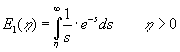(1.15)

Det eksponentielle integral er også kendt fra prøvepumpningsteorien som boringsfunktionen. Grafen er vist i Figur 1.3. Udtrykket (1.14) er en almindelig løsning til grundvandsproblemer i rotationssymmetri, herunder

ligning (1.11). Betingelserne (1.12) er opfyldte siden

går mod 0 når går mod uendelig. Randbetingelsen (1.13) bliver:

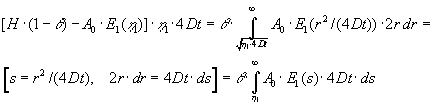(1.16)

Det ses, at tiden t forkortes ud i dette udtryk. Resultatet er en ligning til

bestemmelse sf konstanten :

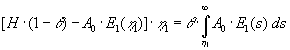(1.17)

Integralet udregnes på følgende måde:

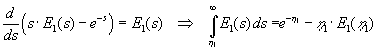Ved indsætelse i (1.17) findes :

(1.18)

Det endelige udtryk for løsningen kan nu ved at kombinere (1.14)

og (1.18) skrives som:

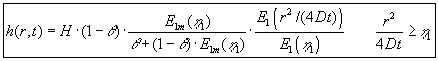(1.19)

Her er introduceret en ny funktion, et modificeret eksponentielt integral:

(1.20)

Grafen for funktionen er vist i Figur 1.2.
1.4 Sænkning i råstofsøen

Sænkningen i søen, findes ved indsættelse af (1.10) i (1.19) og ved anvendelse af (1.4):

(1.21)

Den første faktor er den maksimale sænkning som kun opnås,

når der ikke sker en tilstrømning til graven. Den anden faktor er en funktion

af og . Det noteres, at sænkningen er uafhængig af tiden.

Funktionen (1.20), er vist i Figur 1.2.

Ved at anvende approksimationen (1.27) for det eksponentielle integral, fås

følgende asymptote for små værdier af :

(1.22)

Funktionen er givet ved (1.27).

Approksimationen er behæftet med en fejl mindre end 1% i det angivne

interval, Figur 1.2. For store værdier af fås af (1.28)

den grove approksimation (Figur 1.2, nederst til højre):

(1.23)

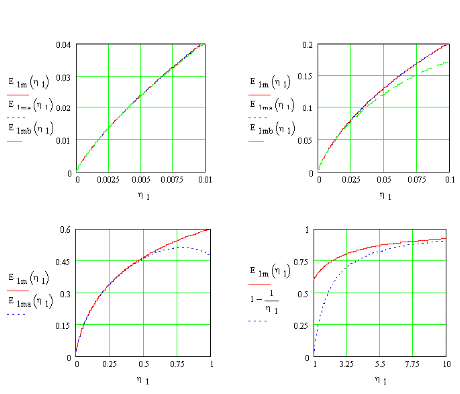
Figur 1.2

Det modificerede eksponentielle integral _1m (1.20) og dets

asymptoter (1.22-.23)

Værdien af er normalt lille i praktiske sammenhænge.

I sådanne tilfælde kan anvendes tilnærmelsen (Figur 1.2, øverst til venstre og til højre):

(1.24)

Her er Euler’s konstant omskrevet for at få den numeriske konstant 0,56,

( ). Fejlen ved approksimationen er igen mindre end 1%

i det angivne interval. Indsættes (1.24) i (1.21) fås følgende udtryk til

beregning af :

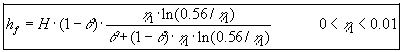(1.25)

Fejlen ved approksimationen er mindre end 1% i det angivne interval for

enhver værdi af porøsiteten . Fejlen er mindre end 5% for

1.5 Sænkning i grundvandsmagasinet

Equation Section (Next)

Sænkningen i grundvandsmagasinet, afhænger af r og t på en

relativt enkel måde. Af (1.19) fås :

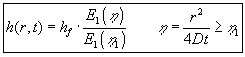(1.26)

Sænkningen i søen, er givet ved (1.21) eller approksimationen (1.25).

Værdien af h er lig for I grundvandsmagasinet varierer h som

.

Figur 1.3 viser og funktionens asymptoter for små og store værdier

af . For små og store værdier af , er disse, (Abramowitz og Stegun,

1964):
(1.27)

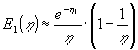(1.28)

Tallet 0.577 er Euler's konstant ( . Fejlen ved

approksimationen (1.27) er under 1% for under 0.002%

for og lig 9% for . De første to led,

er tilstrækkelige for . Den grove tilnærmelse (1.28) viser forløbet

af for store argumenter. Den relative fejl er under 12% for .

Sænkningen i grundvandsmagasinet kan beskrives på følgende

måde. Lad betegne den afstand i hvilken h har aftaget fra

til , hvor p er et tal mellem 0 og 1. Af (1.26) fås:

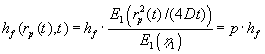(1.29)

eller

(1.30)

For fås den basiske konstant
(1.9).

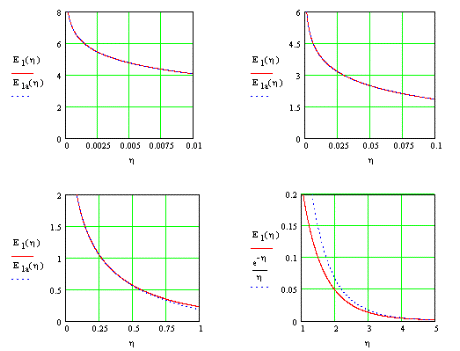Figur 1.3.

Det exponentielle integral (1.15) og dets asymptoter

(1.27-.28).

Sammenligning med pumpning fra en boring

Sænkningen, , omkring en boring, hvorfra der pumpes med konstant

kapacitet (m³/s) er beskrevet ved Theis’ formel:

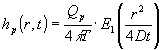(1.31)

Ved sammenligning med (1.26) ses, at de to udtryk er analoge. Tages forholdet mellem de to sænkninger fås

(1.32)

Højre side af (1.32) er et tal, d.v.s der er et fast forhold mellem sænkningerne i grundvandsmagasinet beregnet efter de to metoder.

Indsættes (1.21) i (1.32) og anvendes (1.9) og(1.20), fås med

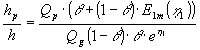(1.33)

For små værdier af fås og , og dermed

Det gælder altså, at for små værdier af kan sænkningerne udenfor graven beregnes ved at anvende den traditionelle Theis formel, hvor

pumpekapaciteten erstattes med ^.

Taleksempel

Equation Section (Next)

Der betragtes et eksempel med følgende data:

H=20 m =0,2 m²/s

m³ s (=1 year)

Heraf fås, (1.3) og (1.9):

m²/s

Af (1.22) og (1.27) fås:

Approximationen (1.24) giver værdien 0.00638. Sænkningen i søen fås af (1.21):

m

Approksimationen (1.25) giver det samme resultat.

Radius i råstofgraven og målet for det påvirkede område bliver (1.8):

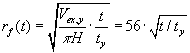m

m

Her er tiden i år. Kvadratet på forholdet mellem de to længder er

parameteren

Sænkningen i grundvandsmagasinet fås af (1.26) . Ved hjælp af (1.27) fås:

m

For eksempel fås:

m

for m

m

for m

m

for m

Disse tre tilfælde svarer i formlerne (1.29-.30) til henholdsvis

⁽⁾ ,

( ) and ( ).

Hvis man i stedet for gravning af 200,000 m³ pr. år opfattede processen som oppumpning af 200,000 m³ grundvand pr. år fås, (1.31), for eksempel

for :

m, år, m

Det tilsvarende resultat ovenfor fås netop ved multiplikation med

[Forside] [Top]