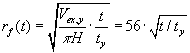|
Følgevirkninger af råstofgravning under grundvandspejlet
Bilag A: Matematisk løsning af vådgravningsproblemet
Det betragtede problem
Udvinding af sand, grus og andre råmaterialer under grundvandsspejlet giver anledning
til sænkninger i den etablerede råstofsø og i grundvandsmagasinet omkring søen. Der
søges en analytisk løsning på problemet med passende forudsætninger for derigennem at
få en forståelse af processerne og bedømme den relative betydning af de ingående
parametre.
Problemet er skitseret i Figur 1.1. Grundvandsmagasinet befinder sig i
| området |
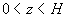 |
, er homogent og isotropt og har |
| uendelig udstrækning. |
Der anvendes rotationssymmetri, d.v.s der udgraves en cirkulær sø, således at
sænkningen h (m) i forhold til begyndelsesniveauet afhænger af r og t.
| Grundvandsmagasinets transmissivitet er |
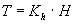 |
, hvor |
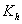 |
er den |
hydrauliske ledningsevne. Gravehastigheden antages at være konstant i tiden, hvilket
betyder at arealet af den blotlagte sø vokser lineært med tiden.
| Radius |
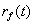 |
af søen vokser følgelig med kvadratroden af tiden. |
| Sænkningen i selve søen, |
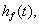 |
er lig med sænkningen i |
| grundvandsmagasinet ved gravefronten. Grundvandsmagasinet har konstant |
| porøsitet |
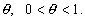 |
Det antages, at alt grundvand forbliver i søen |
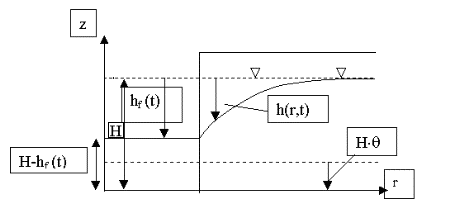
Figur 1.1.
Skematisk illustration af vådgravning.
1.1.1 Opstilling af strømningsligning
Den radiære grundvandsstrømning (m3/m2/s) er, idet det
forudsættes, at sænkningerne er små, d.v.s 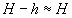
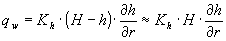 |
(1.1) |
Kontinuitetsligningen svarende til afstanden r og tiden t lyder
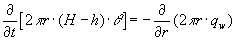 |
(1.2) |
Kombineres disse to ligninger fås strømningsligningen
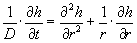 |
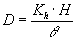 |
(1.3) |
Her betegnes 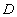 (m2/s)
diffusiviteten. (m2/s)
diffusiviteten.
1.1.2 Global vandbalance
| Sænkningen, |
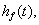 |
i den cirkulære sø , |
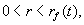 |
| og sænkningen i grundvandsmagasinet er ens ved gravefronten: |
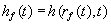 |
(1.4) |
| En global vandbalance bestemmer sænkningen |
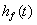 |
: |
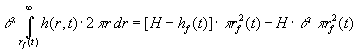 |
(1.5) |
Venstre side udtrykker den vandmængde, der er strømmet fra
| grundvandsmagasinet ( |
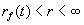 |
) ind i søen. |
| Det første led på højre hånd er vandvoluminet i søen |
(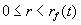 ) ) |
til tiden t, og det andet led er det under gravningen frigivne vand. Det
tidsafledte udtryk for (1.5) kunne også være anvendt, men den integrerede form giver
væsentlige regnelettelser.
| 1.1.3 Ligninger for sænkningen |
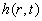 |
Begyndelsessænkningen og sænkningen langt fra graven er 0. Ligningerne for
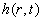 |
er nu, |
(1.3-5): |
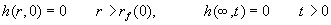 |
(1.6) |
| Gravebetingelserne skal specificeres for at bestemme |
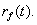 |
|
| En analytisk løsning kan kun findes under særlige vilkår. |
1.2 Konstant gravehastighed
Det antages, at gravehastigheden er konstant, og at gravning starter ved
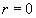 . . |
Dette giver: |
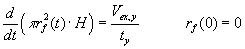 |
(1,7) |
| Her betegner |
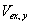 |
(m3) det udgravede volumen gennem en periode |
| (for eksempel 1 år). Det udgravede volumen vokser lineært med tiden, |
| hvilket betyder at |
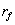 |
er proportional med kvadratroden af tiden: |
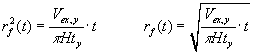 |
(1.8) |
| Faktoren foran t giver en basisk dimensionsløs konstant |
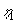 |
: |
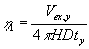 |
(1.9) |
Ved at kombinere (1.8) og (1.9) fås:
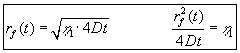 |
(1.10) |
| Parameteren |
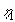 |
er kvadratet på forholdet |
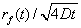 . . |
| Nævneren |
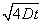 |
er et mål for det påvirkede område til tiden t i forhold |
til kanten af søen. En lille værdi af 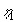 er udtryk for, at radius af det påvirkede område er stort i
forhold til søens radius. er udtryk for, at radius af det påvirkede område er stort i
forhold til søens radius.
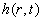 |
bestemmes nu ved løsning af følgende ligninger: |
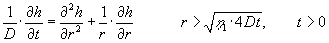 |
(1.11) |
 |
(1.12) |
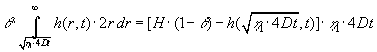 |
(1.13) |
1.3 Analytisk løsning
Der søges en løsning på formen
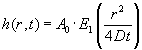 |
(1.14) |
| Her betegner |
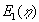 |
det såkaldte eksponentielle integral: |
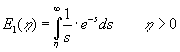 |
(1.15) |
Det eksponentielle integral er også kendt fra prøvepumpningsteorien som
boringsfunktionen. Grafen er vist i Figur 1.3. Udtrykket (1.14) er en almindelig løsning
til grundvandsproblemer i rotationssymmetri, herunder
| ligning (1.11). Betingelserne (1.12) er opfyldte siden |
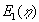 |
| går mod 0 når |
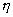 |
går mod uendelig. Randbetingelsen (1.13) bliver: |
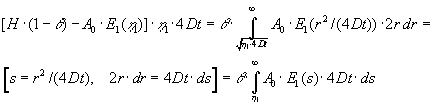 |
(1.16) |
| Det ses, at tiden t forkortes ud i dette udtryk. Resultatet er en
ligning til |
| bestemmelse sf konstanten |
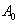 : : |
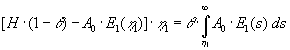 |
(1.17) |
Integralet udregnes på følgende måde:
| Ved indsætelse i (1.17) findes |
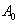 |
: |
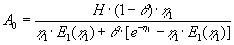 |
(1.18) |
| Det endelige udtryk for løsningen |
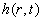 |
kan nu ved at kombinere (1.14) |
| og (1.18) skrives som: |
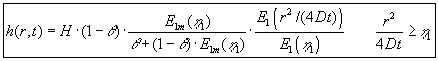 |
(1.19) |
Her er introduceret en ny funktion, et modificeret eksponentielt integral:
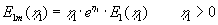 |
(1.20) |
Grafen for funktionen er vist i Figur 1.2.
1.4 Sænkning i råstofsøen
| Sænkningen i søen, |
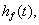 |
findes ved indsættelse |
af (1.10) i (1.19) og ved anvendelse af (1.4):
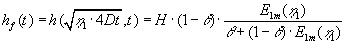 |
(1.21) |
| Den første faktor |
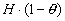 |
er den maksimale |
| sænkning som kun opnås, når der ikke sker en tilstrømning til graven.
Den anden faktor er en funktion |
| af |
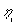 |
og |
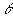 . . |
Det noteres, at sænkningen er |
uafhængig af tiden.
| Funktionen |
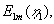 |
(1.20), er vist i Figur 1.2. |
Ved at anvende approksimationen (1.27) for det eksponentielle integral, fås
| følgende asymptote for små værdier af |
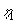 |
: |
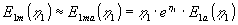 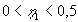 |
(1.22) |
| Funktionen |
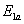 |
er givet ved (1.27). |
Approksimationen er behæftet med en fejl mindre end 1% i det angivne interval, Figur
1.2.
| For store værdier af |
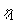 |
fås af (1.28) |
| den grove approksimation (Figur 1.2, nederst til højre): |
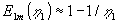 |
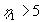 |
(1.23) |
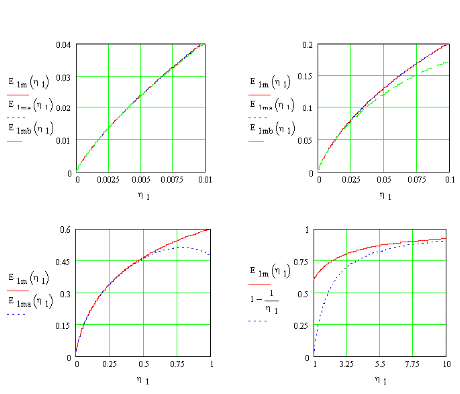
Figur 1.2
| Det modificerede eksponentielle integral |
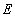 1m 1m |
(1.20) og dets |
| asymptoter (1.22-.23) |
| Værdien af |
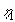 |
er normalt lille i praktiske sammenhænge. |
I sådanne tilfælde kan anvendes tilnærmelsen (Figur 1.2, øverst til venstre og til
højre):
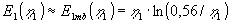 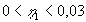 |
(1.24) |
Her er Euler’s konstant omskrevet for at få den numeriske konstant 0,56,
| ( |
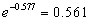 |
). Fejlen ved approksimationen er |
igen mindre end 1% i det angivne interval. Indsættes (1.24) i
(1.21) fås følgende udtryk til beregning af 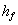 : : |
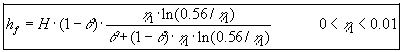 |
(1.25) |
| Fejlen ved approksimationen er mindre end 1% i det angivne
interval for. |
| enhver værdi af porøsiteten |
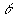 |
| Fejlen er mindre end 5% for |
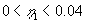 |
1.5 Sænkning i grundvandsmagasinet
| Sænkningen i grundvandsmagasinet, |
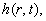 |
afhænger |
af r og t på en relativt enkel måde . Af
(1.19) fås : |
| |
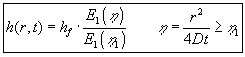 |
(1.26) |
| Sænkningen i søen, |
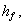 |
er givet ved (1.21) eller approksimationen (1.25). |
| Værdien af h er lig |
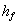 |
for |
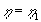 |
I grundvandsmagasinet varierer h som |
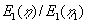 . . |
|
|
|
|
| Figur 1.3 viser |
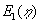 |
og funktionens asymptoter for små og store værdier |
| af |
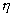 . . |
For små og store værdier af |
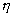 , , |
er disse, (Abramowitz og Stegun, 1964): |
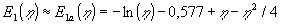 |
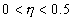
|
(1.27) |
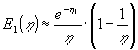 |
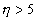 |
(1.28) |
| Tallet 0.577 er Euler's konstant ( |
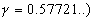 |
. Fejlen ved |
| approksimationen (1.27) er under 1% for |
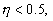 |
under 0.002% |
| for |
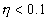 |
og lig 9% for |
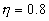 |
. De første to led, |
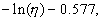 |
| er tilstrækkelige for |
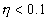 |
. Den grove tilnærmelse (1.28) viser forløbet |
| af |
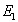 |
for store argumenter. Den relative fejl er under 12% for |
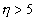 . . |
| Sænkningen |
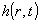 |
i grundvandsmagasinet kan beskrives på følgende |
| måde. Lad |
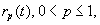 |
betegne den afstand i hvilken h har aftaget fra |
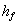 |
til |
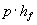 |
, hvor p er et tal mellem 0 og 1. Af (1.26) fås: |
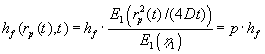 |
(1.29) |
eller
 |
(1.30) |
| For |
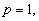 |
fås den basiske konstant |
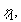 |
(1.9). |
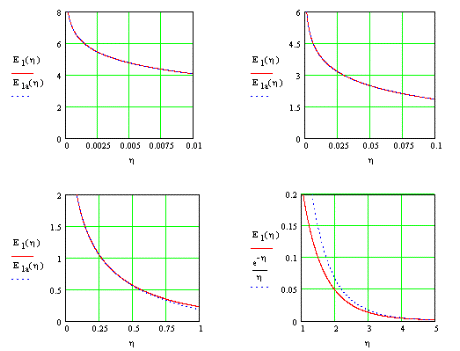
Figur 1.3.
Det exponentielle integral 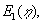 (1.15) og dets asymptote(1.27-.28). (1.15) og dets asymptote(1.27-.28).
1.6 Sammenligning med pumpning fra en boring
Sænkningen 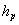 , omkring
en boring, hvorfra der pumpes med konstant kapacitet , omkring
en boring, hvorfra der pumpes med konstant kapacitet 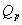 (m3/s) er beskrevet ved Theis’ formel: (m3/s) er beskrevet ved Theis’ formel:
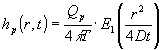 |
(1.31) |
Ved sammenligning med (1.26) ses, at de to udtryk er analoge. Tages forholdet mellem de
to sænkninger fås
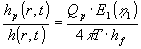 |
(1.32) |
Højre side af (1.32) er et tal, d.v.s der er et fast forhold mellem sænkningerne i
grundvandsmagasinet beregnet efter de to metoder.
| Indsættes (1.21) i (1.32) og anvendes (1.9) og(1.20), fås med |
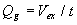 |
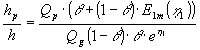 |
(1.33) |
| For små værdier af |
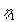 |
fås |
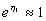 og og |
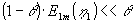 |
|
og , og dermed
Det gælder altså, at for små værdier af 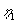 kan
sænkningerne udenfor graven beregnes ved at anvende den traditionelle Theis formel, hvor kan
sænkningerne udenfor graven beregnes ved at anvende den traditionelle Theis formel, hvor
| pumpekapaciteten |
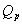 |
erstattes med |
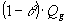 . . |
Taleksempel
Der betragtes et eksempel med følgende data:
| H=20 m |
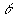 |
=0,2 |
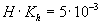 |
m2/s |
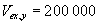 |
m3 |
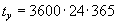 |
s (=1 year) |
Heraf fås, (1.3) og (1.9):
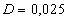 |
m2/s |
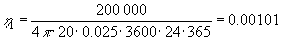 |
Af (1.22) og (1.27) fås:
Approximationen (1.24) giver værdien 0.00638. Sænkningen i søen fås af (1.21):
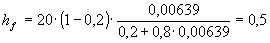 |
m |
Approksimationen (1.25) giver det samme resultat.
| Radius i råstofgraven og målet |
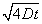 |
for det påvirkede område bliver (1.8): |
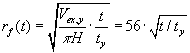 |
m |
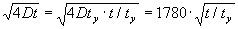 |
m |
| Her er |
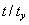 |
tiden i år. Kvadratet på forholdet mellem de to længder er |
| parameteren |
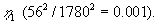 |
Sænkningen i grundvandsmagasinet fås af (1.26) . Ved hjælp af (1.27) fås:
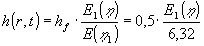 |
m |
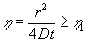 |
For eksempel fås:
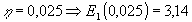 |
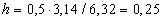 |
m |
| for |
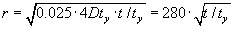 |
m |
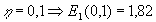 |
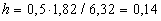 |
m |
| for |
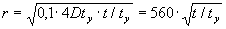 |
m |
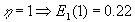 |
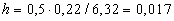 |
m |
| for |
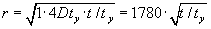 |
m |
Disse tre tilfælde svarer i formlerne (1.29-.30) til henholdsvis
Hvis man i stedet for gravning af 200,000 m3 pr. år opfattede processen som
oppumpning af 200,000 m3 grundvand pr. år fås, (1.31), for eksempel
| for |
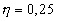 |
: |
| Det tilsvarende resultat ovenfor fås netop ved
multiplikation med |
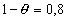 |
|

![]()
![]() (m2/s)
diffusiviteten.
(m2/s)
diffusiviteten.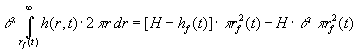
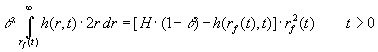
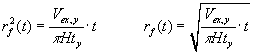

![]() er udtryk for, at radius af det påvirkede område er stort i
forhold til søens radius.
er udtryk for, at radius af det påvirkede område er stort i
forhold til søens radius.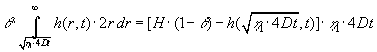
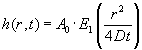
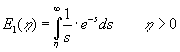
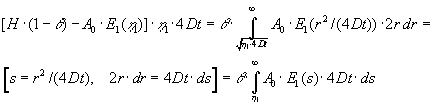
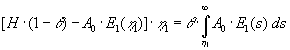
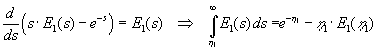
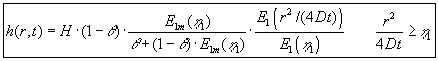

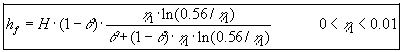
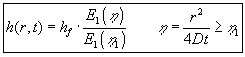
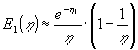
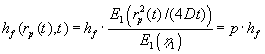

![]() (1.15) og dets asymptote(1.27-.28).
(1.15) og dets asymptote(1.27-.28).![]() , omkring
en boring, hvorfra der pumpes med konstant kapacitet
, omkring
en boring, hvorfra der pumpes med konstant kapacitet ![]() (m3/s) er beskrevet ved Theis’ formel:
(m3/s) er beskrevet ved Theis’ formel: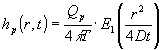
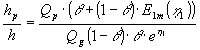
![]() kan
sænkningerne udenfor graven beregnes ved at anvende den traditionelle Theis formel, hvor
kan
sænkningerne udenfor graven beregnes ved at anvende den traditionelle Theis formel, hvor