|
Kortlægning af diffus jordforurening i byområder. Delrapport 3 Bilag
A
|
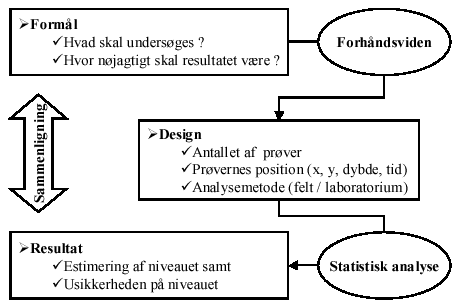
Element i Figur 1 |
Uddybende forklaring |
Formål |
At beskrive niveauet af ét eller flere stoffer indenfor et afgrænset område (også at vurdere niveauet hvor der ikke er udtaget prøver). Endvidere bør nævnes hvilke konsekvenser forskellige resultater vil få. |
Hvad skal undersøges ? |
Koncentrationen af stof X, f.eks. angivet (mg X/g TS). |
Hvor nøjagtigt skal resultatet være |
Det skal kunne vurderes om stof X overstiger en given grænseværdi. Der ønskes derfor et konfidensinterval omkring de estimerede værdier. Usikkerheden på estimatet er faktisk mere interessant end estimatet ! |
Forhåndsviden |
Er der tidligere lavet undersøgelser i samme område inddrages informationer fra disse. Historiske oplysninger om arealanvendelse kan give oplysninger om forureningskilder. Undersøgelser fra lignende områder kan give indtryk af variationen i niveauet. Hvad er baggrundsniveauet og variation i ikke-forurenet jord ? |
Design |
Beskriver undersøgelsesområdet, antallet af prøver der skal undersøges, hvornår de skal foretages samt hvordan de skal analyseres. |
Antallet af |
Hvor mange prøver skal der undersøges. |
Prøvernes position (x, y, dybde, tid) |
Prøvernes position indenfor det geografiske område samt dybden hvorfra de skal udtages. Endvidere bør prøvetagningstidspunkt for de enkelte prøver fremgå. Et formål kunne være at følge udvikling over tid. |
Analysemetode (felt / laboratorium) |
Skal prøverne analyseres med flere metoder ? |
Statistisk analyse |
Der er to dele i en statistisk analyse, en beskrivelse af data og en statistisk model af niveauet baseret på data. Den beskrivende del indeholder generelle deskriptive størrelser, samt en beskrivelse af den geografiske variation. Kvantitativ og visuel inspektion. Model beskrivelsen udnytter den geografiske variation i data til at estimere niveauet samt usikkerheden på dette i hele området. Dette kan gøres på forskellige måder. Modellerne anvender vægtede interpolations-metoder baseret på målinger i nærheden. Måden de omkringliggende observationer udnyttes på er, alt andet lige, afgørende for resultatet. Det bemærkes at "alle modeller er forkerte men nogle er brugbare" |
Resultat |
Angives ofte som et interpoleret kontur-kort |
Estimat af niveauet |
Angivelse af koncentrationen af stof X i hele området. |
Usikkerheden på niveauet |
Usikkerheden på angivelsen, oftest som en standard afvigelse eller et konfidensinterval |
2.1 Forureningskilder
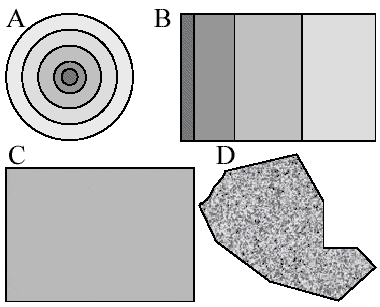
Diffus jordforurening kan stamme fra en eller flere kilder. Det er ikke muligt at præsentere et generelt design til undersøgelse af diffus jordforurening idet kilderne til diffus jordforurening kan variere mellem områder samt indenfor områder. I Figur 2 er angivet eksempler på udbredelsen af forskellige former for diffus jordforurening Disse kunne stamme fra forskellige kilder
Figur 2
Forskellige forureningstyper, mørk farve indikerer høj koncentration og lys lav
koncentration. A: Punktkilde, B: Linjekilde, C: Overfladekilder, D: Mange små tilfældige
kilder.
Different pollutant types: Dark and light colours indicate high and low concentrations
respectively. A. Point sources. B. Line sources. C. Uniform surface sources. D. Many small
haphazard sources.
Beskrivelsen i Figur 2 er ikke udtømmende og variationerne er uendelige. Variationer over A kunne være en ellipse, eller et cirkel udsnit forårsaget af vind eller andre påvirkninger. Variationer over B kunne være en krum linje hvor deponering/niveauer ikke fordeltes jævnt med afstanden, indflydelse af bygninger mv. Variationer over C kunne være parceller hvor forureningen er ens indenfor parceller og forskellig mellem parceller. Variationer over D kunne være lokale områder der er mere homogene end andre eller lokale områder med varierende koncentrationer grundet forskellig oprindelse.
Der vil i sagens natur skulle anvendes forskelligt stikprøveplaner for at kunne beskrive variationen i de scenarier beskrevet i Figur 2. Det er derfor vigtigt (ikke overraskende) at forhåndsviden om området inddrages i planlægning af undersøgelsen. Med den historiske arealanvendelse, resultater fra eventuelle tidligere undersøgelse, meteologiske forhold samt øvrige relevante oplysninger bør der kunne dannes en forestilling om, hvordan forureningen varierer indenfor området.
Denne forestilling bør formuleres som en hypotese:
| Eksempel I) Det antages at blyindholdet i jorden aftager med afstanden fra vejen, den sydlige ende af arealet vurderes mindre belastet grundet afskærmning mod vejen. |
| Eksempel II) Jorden antages at være opblandet i en sådan grad at der ikke er nogen struktur i koncentrationsniveauet. Der vurderes at være en tilfældig fordeling af koncentrationsniveauet i området. Dog antages det, baseret på tidligere undersøgelser, at niveauet er under grænseværdien. |
Hypoteserne beskrevet i eksempel I og II bør lede til to forskellige forsøgsplaner. Fra I) bør der kunne vurderes om trenden er som beskrevet og fra II) skal der undersøges om der findes koncentrationer over grænseværdien. I det efterfølgende uddybes betydningen af forsøgsdesignets indflydelse på vurderingen af den spatielle variation.
2.2 Indflydelse af forsøgsdesign på koncentrationsbestemmelse og usikkerhed
Som det vil fremgå af beskrivelsen af de statistiske værktøjer, der anvendes til at beskrive de data der fremkommer fra analyserne, er der en række egenskaber ved forsøgsdesignet der har betydning for estimationen af niveauet og usikkerheden på dette.
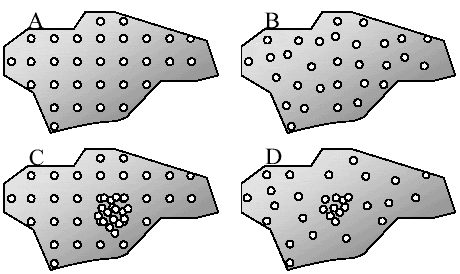
Det optimale design i forhold til estimationen er desværre ikke optimalt i forhold til usikkerheden på denne. I Figur 3 er skitseret en hypotetisk diffus jordforurening. Gråtoningen beskriver niveauet af det undersøgte stof (mørk=høj, lys=lav). Der er en diagonal trend fra øverste venstre hjørne mod nederste højre hjørne. De hvide cirkler angiver punkter, hvor der udtages prøver.
Figur 3
Forskellige undersøgelsesplaner.
Different investigation strategies
I A, C, D er udtaget prøver fra 30 positioner, hvor der i C er udtaget prøver fra 48 positioner. I A er et fastnet med ens afstand l mellem alle positioner, i B er positionerne tilfældige, i C et fast net med ens afstand l mellem alle positioner tilføjet 18 tilfældige positioner indenfor et begrænset område og i D er positionerne tilfældige dog er 10 positioner indenfor et begrænset område.
I det følgende vil blive beskrevet hvilken indflydelse de forskellige designs A-D har på den videre analyse af data. Alle spatielle analyser udnytter at målinger fra positioner tæt på hinanden er mere ens end målinger fra positioner langt på hinanden. Udtages der prøver "lige ved siden af hinanden" forventes det at prøver har stor lighed (er korrelerede). Prøver udtaget i hver sin ende af området forventes derimod ikke nødvendigvis at være ens. Afstanden mellem observationerne er omdrejningspunktet i det følgende
Variansen af målingerne kan anvendes som et mål for "ensheden" (en lille varians mellem observationer/målinger betyder de er meget ens/korrelerede og en stor varians mellem observationer/målinger betyder de er meget forskellige ens/ikke-korrelerede). Første trin i en vurdering af variansens afhængighed af afstanden mellem målepositionerne er at dele den maksimale afstand mellem to målinger i eksempelvis 10 intervaller (maksimal afstand 1000m; der inddeles i intervaller af 100m). Andet trin er at finde alle kombinationer af to målepunkter der har en indbyrdes afstand indenfor hvert af de pågældende intervaller (30 par i intervallet fra 0-100m, 47 par i intervallet fra 100-200m, …, 12 par i intervallet fra 900-1000m ). Tredje trin er at beregne variansen af punkterne i hvert af intervallerne. (variansen af de 30 par i intervallet 0-100m, variansen af de 47 par i intervallet 100-200m, …, variansen af de 12 par i intervallet fra 900-1000m). Herved kan man vurdere om variansen vokser med afstanden mellem observationerne. En væsentlig ting at bemærke er at vurdering af variansen indenfor afstande mindre end afstanden mellem de to nærmeste punkter er gætteri. Der fastlægges altså et minimumsvariationsniveau ud fra de nærmeste punkter i analysen. Med andre ord er vurdering af variationer på en skala mindre end denne afstand ekstrapolation. Derfor er den generelle opfattelse, blandt geostatistikere, at det er vigtigt at have nogle målinger meget tæt på hinanden samt gerne gentagne målinger på samme position (evt samme prøve). Se endvidere afsnittet på geografisk korrelation.
Betragtes figur 3 eksempel A vil det ikke være muligt at vurdere den spatielle variation på en skala mindre end maskestørrelsen i "nettet". I figur 3 eksempel B er det muligt at vurdere den spatielle variation fra en skala svarende ca. til den mindste afstand af de tilfældige placerede målinger. I figur 3 eksempel C og D opnås der derimod information om variationen på langt mindre skala (afstand). Denne information er vigtig for at kunne minimere usikkerheden på estimationen.
Relateres Figur 2 og Figur 3 kan følgende opsummeres. Det anvendte forsøgsdesign skal afspejle den hypotese der er beskrevet for området. Forventes en forureningsfane skal der foretages målinger i fanen så dens udbredelse kan følges. Omvendt forventes forureningen at være af mere tilfældig karakter, er der ikke grund til at prøverne skal udtages på bestemt positioner. Variationen mellem de nærmeste punkter bliver et minimumsvariansniveau og en minimumsinterpolationsafstand. Disse betragtningerne om variation uddybes i afsnittet om geografisk korrelation.
3. Analyse
3.1 Deskriptiv statistik
Som i enhver anden statistisk analyse bør der indledes med en række deskriptive mål og som minimum: Antal data, Fraktiler (minimum, median og maksimum), middelværdi og spredning, histogrammer samt fordelingsplot. Se et eksempel i bilag B.
Hvis de enkelte jordprøver er analyseret for flere forskellige stoffer bør korrelationen mellem enkeltstofferne beregnes. En høj korrelationskoefficient (tæt på 1 henholdsvis -1) betyder at to stoffer er positivt henholdsvis negativt korrelerede. En lav korrelationskoefficient (numerisk tæt på 0) betyder at der ikke er sammenhæng mellem de to enkeltstoffer. Se et eksempel i bilag B.
Er der målt mange enkeltstoffer kan forskellige multivariate teknikker eksempelvis principal komponent analyse (PCA) , Min/Max Autocorrelation Factors (MAF) anvendes til at beskrive korrelation af de stoffer der er interessante (Nielsen 1994, Andersen 1994). Derved kan man reducere dimensionen af datasættet. Teknikkerne beregner nye variable, der er linear kombinationer af de oprindelige måleparametre. Disse nye uafhængige variable kan så anvendes i en spatiel analyse. Anvendelse af disse metoder samt tolkningen resultaterne bør foretages af statistikere og miljø/forurenings eksperter i fælleskab.
3.2 Spatiel statistik (geostatistik)
Der findes forskellige statistiske metoder, der estimerer den geografiske varians/korrelationsstruktur udfra målingerne og udnytter denne i interpolationen mellem målepunkterne samt beregner usikkerheden på interpolationsresultatet.
Disse metoder antager og udnytter, at observationer i nærheden af hinanden er korrelerede mere korrelerede en observationer langt fra hinanden (modsat standard statistiske analyser der antager at observationerne er uafhængige).
3.2.1 Geografisk korrelation
Den geografiske varians/korrelationsstruktur i data kan beskrives på forskellig vis. To principielt forskellige mål anvendes hyppigt.
- Det simple mål tester om data kan antages at være uafhængige af geografien (afstande) og er derfor ikke umiddelbart anvendeligt til beregninger.
- Det mere komplicerede mål kvantificerer variansens (eller korrelationens) afhængighed af afstanden.
ad 1)
Som test for geografisk uafhængighed kan anvendes Moran’s I , der tester hypotesen om "ingen spatiel korrelation" (Cliff and Ord, 1973, 1981; Anselin 1995). Moran’s I beskriver korrelationen mellem "naboer". En stor værdi af Moran’s I betyder positiv korrelation og en lille (negativ) værdi betyder negativ korrelation. Det kan testes om (Moran’s I ) korrelationen er signifikant. Resultatet af analysen er udelukkende et ja/nej svar til om der er spatiel korrelation eller ej, der fremkommer ikke noget udtryk der beskriver korrelationens afhængighed af afstanden mellem observationerne
ad 2)
Variogrammer er hyppigt anvendt til at kvantificere den geografiske afhængighed. Der knytter sig normalt 3 parametre til et variogram. De beskriver egenskaber ved variogrammet og betegnes nugget, sill og range (Cressie 1991, Ripley 1988, Diggle 1983).
Nugget er en sum af flere komponenter der med en snedig forsøgsplan kan adskilles, den består af måleusikkerheden samt den variation der er mellem to prøver taget meget tæt på hinanden. Måle usikkerheden kan estimeres ved at lave flere bestemmelser på samme prøve og variationen mellem prøver med meget lille indbyrdes afstand kan estimeres ved at udtage prøver med meget lille afstand.
Sill er den maksimale variation, det vil sige den variation der er i data stammende fra målepunkter med så stor indbyrdes afstand at de er uafhængige.
Denne afstand hvor målingerne ikke længere er korrelerede, dvs. uafhængige kaldes range.
Forholdet (Sill - Nugget)/Nugget er af stor betydning for den videre anvendelse af variogrammet til for eksempel kriging. Variogrammet beregnes ved at inddele afstanden mellem observationerne i en række intervaller. Dernæst beregnes variansen mellem alle observationer i det pågældende interval. Disse varianser plottes derefter mod afstanden mellem observationer som skitseret i nedenstående Figur 4, Nugget, Sill og Range er ligeledes skitseres.
Det er nærliggende at tilpasse (fitte) en kurve til punkterne i variogrammet. Der eksisterer adskillige variogrammodeller – de oftest anvendte er en gaussisk, eksponentiel eller sfærisk funktion (Cressie 1991, Ripley 1983, Diggle Nielsen 1994, Andersen 1994). Parametrene der beskriver disse kurver er netop nugget, sill og range. Der anvendes ofte en vægtet mindste kvadraters metode til at fitte disse funktioner. Der vægtes ofte med antallet af punkter der ligger til grund for de enkelte varians punkter.
Her bør det påpeges at den tilpassede kurve og dermed estimationen af nugget, sill og range vil være afhængig af valget af antal intervaller. Den tilpassede kurve udgør nu det bedste bud på variations afhængighed af afstanden mellem observationer. Den tilpassede variogramkurve benyttes som en vægt i interpolationsmetoden kaldet kriging. Det er altså den aktuelle geografiske variation som data udviser der bestemmer med hvilken vægt de skal indgå i analysen, modsat standard interpolationsmetoder som "Nærmeste nabo" eller Euklidisk afstand" hvor der ikke tages hensyn til den struktur data udviser.
Stejlheden af variogrammet beskriver hvor hurtigt variansen/korrelationen ændrer sig
Variogrammet bør estimeres i forskellige retninger, så udelukkende målepunkter i en vis retning kommer i betragtning eks. (0° ,45° ,90° ,135° ). Endvidere kan området inddeles i delområder og variogrammet kan estimeres indenfor hvert delområde. Inddeles området i en række delområder bliver det naturligvis på bekostning af antallet af observationer i området.
Den væsentligste indvending mod at anvende traditionel kriging som interpolationsmetode er at variogrammet er afhængig af størrelsen af de valgte intervaller. Dette diskuteres yderligere i efterfølgende afsnit om estimation og kriging.
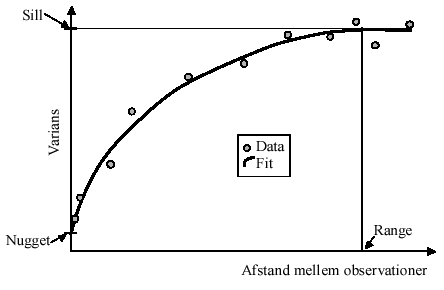
Figur 4
Teoretisk variogram
Theoretical variogram
3.2.2 Estimation og kriging
I dette afsnit vil der blive præsenteret to forskellige måder ( interpolationsmetoder) at estimere niveauet af ét enkelt stof inden for et geografisk område, her betegnet Kriging (Cressie 1991, Ripley 1988, Diggle 1983, Nielsen 1994, Andersen 1994) og Likelihood (Diggle and Ribeiro 2000, 2001; Christensen, Diggle and Ribeiro 2000, 2001). De to metoder er skitseret i det følgende
- Vælg en maksimal afstand og inddel afstanden i antal intervaller.
- Estimer variogrammet, dvs. variationen indenfor hvert afstandsinterval
- Estimer parametrene i en variogramfunktion (nugget, sill og range).
- Benyt variogramfunktionen i kriging til at estimere niveauet
- Benyt "kriging standard error" til at beregne et konfidensinterval for estimatet
Resultatet er at der på basis af de målte værdier beregnes koncentrationsintervaller for forureningen (enkeltstoffer) over området som helhed.
I simpel/ordinær kriging prædikteres værdierne udelukkende baseret på variogrammet, hvor data vægtes i forhold til den fittede variogram funktion. Dvs. variogrammet benyttes til at forudsige både global og lokal variation.
I universel kriging fittes en n'te grads model til data og der foretages ordinær kriging af residualerne, addition af disse giver den predikterede værdi. n'te grads modellen beskriver den globale variation (eks. trend) og kriging af residualerne beskriver den lokale variation (afvigelser fra trenden).
Et specialtilfælde af universel kriging er ordinær kriging hvor n=0, dvs et niveau samt kriging af residualerne. Usikkerheden på prediktionen i universel kriging er usikkerheden på kriging af de spatielt korrelerede residualer adderet til usikkerheden på n'te grads polynomiet. Der benyttes almindelige statistiske betragtninger til at vurdere hvordan parametrene (orden af polynomiet), skal vælges (Venables and Ripley 1999, Cressie 1991)
- Vælg en variogram funktion
- Estimer niveauet samt parametrene i variogramfunktionen (nugget, sill og range).
- Benyt "standard error" til at beregne et konfidensinterval for estimatet
3.2.3 Valg af metode
Udfra en statistisk betragtning bør Likelihood metoden vælges idet den er uafhængig af valg af intervaller og er derfor at foretrække. Desværre er denne metode ikke så velkendt eller anvendt af andre end statistikere (Diggle and Ribeiro 2000, 2001; Software geoR).
Udfra en praktisk synsvinkel og med den store mængde programmer der kan estimere semivariogrammer og foretage kriging vil denne metode være at foretrække
Der vælges den variogram funktion der ud fra almindelige statistiske betragtninger giver det bedste fit.
En ofte anvendt metode at slette enkelte datapunkter og dernæst estimere dem med kriging og kigge på forskellen mellem det målte og det estimerede (Cressie 1991, Andersen 1994).
4. Diskussion
Som beskrevet i afsnit 2 er designet afhængig af den hypotese, der er generet om den diffuse jordforureningsudbredelse samt formålet med analysen. Den væsentligste forskel ligger i om formålet er at estimere niveauet i hele det geografiske område eller der udelukkende ønskes en sandsynliggørelse af om en given grænseværdi overskrides.
Det vil til tider kunne betale sig at lave et faseopdelt undersøgelsesprogram med henblik på et dynamisk forsøgsdesign som skræddersyes/optimeres trinvis. Dette ville givetvis have været fornuftigt i eksemplet gennemarbejdet i bilag B.
Det er en fordel at udpege delarealer, hvor der kan forventes kritiske værdier, idet dette giver information om det maksimale niveau af den observerede størrelse.
4.1 Valg af software
Haves data i et GIS (MAPINFO, ARCVIEW, IDRISI) kan de tilhørende spatielle add-in’s benyttes til de geostatistiske analyser. På web adressen http://www.ai-geostats.org/ er en glimrende oversigt over alverdens forskellige programmer, samt henvisninger til litteratur.
Til analyserne i bilag B er anvendt GeoR: http://www.maths.lancs.ac.uk/~ribeiro/geoR.html
En løftet pegefinger: Pas på automatiserede interpolationsprogrammer idet disse ikke altid giver mulighed for at vurdere de underliggende forudsætninger.
5. Referenceliste
5.1 Litteratur
Andersen J.S. (1994). Flerdimensionale rumligt korrelerede forureningsdata, IMM, DTU. Eksamensprojekt 1994-28, ISSN 0909-6256.
Anselin L. (1995). Local indicators of Spatial Association – LISA. Geographical Analysis.; 27 (2):93-115.
Christensen, O.F. Diggle P.J. and Ribeiro J.R. (2001). Analysing positive-valued spatial data: the transformed Gaussian model. I Monestiez, P., Allard, D. and Froidevaux (eds), GeoENV III - Geostatistics for environmental applications. Quantitative Geology and Geostatistics, Kluwer Series, 11, 287--298.
Cressie N.A. (1991). Statistics for Spatial Data Wiley and Sons.
Diggle P.J. (1983). Statistical analysis of spatial point patterns. Academic press, London.
Diggle P.J. and Ribeiro J.R. (2000). Model-based geostatistics. Caxambu: Associação Brasileira de Estatística. (14º SINAPE - Simpósio Nacional de Probabilidade e Estatística).
Diggle P.J. and Ribeiro J.R. (2001). Bayesian inference in Gaussian model-based geostatistics. Geographical and Environmental Modelling (to appear)
Nielsen, A.A. (1994). Analysis of Regularly and Irregularly Sampled Spatial, Multivariate, and Multi-temporal Data. Ph.D. Thesis No. 6, Department of Mathematical Modelling, Technical University of Denmark
Cliff A.D. and Ord J.K. (1973). Spatial autocorrelation. London: Pion Ltd..
Cliff A.D. and Ord J.K. (1981). Spatial processes, Models and applications. London: Pion Ltd.
Ribeiro JR, and Diggle PJ. (1999). geoS: A geostatistical library for S-PLUS. Technical report ST-99-09, Dept of Maths and Stats, Lancaster University.
Ripley B. D. (1988) Statistical inference for spatial processes. Cambridge University Press. Cambridge
Venables W.M. and Ripley B. D (1999). Modern applied statistics with S-plus. 1999 Springer, New York.
5.2 Software
http://www.ai-geostats.org/
http://www.maths.lancs.ac.uk/~ribeiro/geoR.html