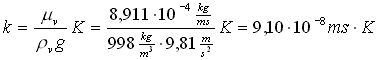| Forside | | Indhold | | Forrige | | Næste |

Modellering af opvarmning ved dampinjektion (Modi)

7. Parametervalg

Jord er per definition altid heterogen, og det kan derfor være svært at finde repræsentative værdier for de nødvendige parametre. Samtidig er det omkostningskrævende at foretage målinger, og man må derfor altid foretage en afvejning af, hvor meget der skal måles for, at man med rimelig sikkerhed kan træffe de nødvendige beslutninger.

Den udviklede model giver gode muligheder for at foretage en sensitivitetsanalyse af de enkelte parametre, så man kan få en ide om deres indbyrdes betydning og derved afgøre, hvilke der skal bestemmes med hvilken præcision.

Det anbefales at forsøge med forskellige værdier for alle centrale parametre for at vurdere usikkerheden på resultaterne.

7.1 Permeabilitet

Permeabiliteterne er langt de vigtigste parametre i modellen, eftersom de bestemmer dampzonens form. Derudover bestemmer de, hvor meget damp der kan injiceres, før trykket overstiger trykket fra den ovenliggende jord. Forholdet mellem den vertikale og den horisontale permeabilitet bestemmer, hvor langt en dampzone kan nå ud, før den bryder igennem jordoverfladen. Derfor vil dette forhold ofte være bestemmende for, hvor stor afstand der kan være mellem injektions- og ekstraktionsboringer i forhold til dybden af de jordlag, der ønskes opvarmet. Som oftest vil den horisontale permeabilitet være større end den vertikale, og en dampzone vil derfor primært udbrede sig i horisontal retning.

I modellen benyttes permeabiliteten for gasfasen, hvilket er den permeabilitet, der måles ved en vakuumtest. I tilfælde hvor vandindholdet er meget højt i den umættede zone, vil en vakuumtest undervurdere permeabiliteten for dampen, idet dampen på grund af højere tryk er i stand til at fortrænge en del af vandet.

Permeabiliteten målt under grundvandsspejlet ved en pumpetest vil til praktiske formål også være nøjagtig nok at anvende.

Det anbefales altid at bestemme permeabilitet og helst på en sådan vis, at der kan skelnes mellem horisontal og vertikal permeabilitet.

Bemærk i øvrigt, at enheden på permeabiliteten (k) er m², og det er altså ikke den hydrauliske ledningsevne, der skal angives. Følgende formel kan benyttes til omregning:

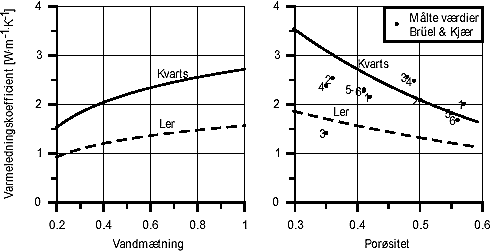
hvor k er permeabiliteten, K er den hydrauliske ledningsevne i m·s^-1, og r _v og m _v er vands densitet og viskositet ved 25 °C.

7.2 Grundvandsspejl

Der er stor forskel på dampzonens udbredelse over og under grundvandsspejlet, og det er derfor vigtigt at kende dets nøjagtige placering. Det kan imidlertid være svært, eftersom dampinjektion sædvanligvis ledsages af grundvandsoppumpning. Grundvandsspejlet vil derfor variere både over tid og over sted. Man bør derfor forsøge med forskellige simuleringer, hvor dybden til grundvandsspejlet varieres.

Det skal understreges, at det er forbundet med væsentligt større usikkerhed at simulere dampinjektion under grundvandsspejlet end over. Det skyldes, at modellen ikke direkte tager højde for grundvandets strømning.

7.3 Injektionsrate/tryk

Der kan angives både en maksimal injektionsrate og et maksimalt injektionstryk, som ikke kan overskrides i løbet af simuleringen. Den maksimale injektionsrate vil ofte være bestemt af anlægget til produktion af damp, mens det maksimale injektionstryk kan være bestemt af de overliggende jordlags tryk. I modellen beregnes et vejledende maksimalt injektionstryk ud fra vægten af jordlagene over toppen af filteret, og det anbefales at holde en vis sikkerhedsmargen til denne værdi. I beregningen indgår vægten af eventuelt grundvand. Hvis injektionstrykket overstiger jordens tryk, kan der dannes sprækker i jorden, hvilket er problematisk.

Hvis der benyttes to filtre, og injektionsraten sættes til 0 i det øverste filter bliver filterlaget en del af det øverste lag. Det vil sige, at det får den samme permeabilitet både horisontalt og vertikalt. Derved er der mulighed for at simulere en situation, hvor geologien over injektionsfilteret beskrives ved to forskellige geologiske lag. Det kræves, at filterlaget har en tykkelse svarende til 3 gange diskretiseringen, eftersom filterlaget normalt opløses i tre celler.

En anden mulighed, når der er to filtre, er at indsætte et tilfældigt negativ tal som injektionsrate i det nederste filter. I det tilfælde benyttes injektionsrate og –tryk for det øverste filter i hele boringen, og dampen fordeles mellem de to filtre i forhold til filterlængde, permeabilitet og tryk foran det pågældende filter. Den funktion kan benyttes, når boringen er filtersat over to forskellige geologiske lag.

7.4 Varmeledningskoefficient

Som tidligere beskrevet er varmeledningskoefficienten for jord bestemt af typen og fordelingen af mineralkorn, porøsiteten og vandindholdet. Sundberg (1988) /7/ angiver nogle empiriske formler til beregning af varmekapaciteten, hvilket er illustreret i nedenstående figurer for to jordtyper.

Figur 7.1
Varmeledningskoefficient for jord som funktion af vandmætning og porøsitet for to jordtyper. Punkterne på figuren til højre er målte værdier fra Brüel & Kjær-grunden. Tallene refererer til prøvenummer. Data fra /8/

Figuren til venstre viser varmeledningskoefficienten som funktion af vandindholdet for to jordtyper med porøsiteten 0,4, og figuren til højre viser den tilsvarende afhængighed af porøsiteten for de to jordtyper ved fuld vandmætning. Varmeledningskoefficienten stiger med vandmætning, hvilket skyldes, at vand leder varmen bedre end luft. Tilsvarende leder mineralkornene varmen bedre end vand, hvilket ses ved, at varmeledningskoefficienten falder ved stigende porøsitet. De tilsvarende kurver for sand, silt og moræneler ligger imellem de to viste kurver. På figuren til højre er ligeledes vist nogle måleresultater fra Brüel & Kjær-grunden. Der var udtaget seks prøver, hvorpå varmeledningskoefficienten blev bestemt ved to forskellige porøsiteter. Der er en forholdsvis stor spredning på værdierne, hvilket nok skyldes måleusikkerhed. For prøve nummer tre og fire stiger varmeledningskoefficienten med porøsiteten, hvilket ikke er logisk.

De udsving, der er på varmeledningskoefficienten, vil i det generelle tilfælde ikke have stor indflydelse på opvarmningen ved dampinjektion. Udsvingene imellem forskellige jordtyper ses også at være forholdsvis begrænset, og det kan derfor ikke anbefales, at man udtager jordprøver til bestemmelse af varmeledningskoefficienten i forbindelse med en dampoprensning.

Det anbefales, at der benyttes en varmeledningskoefficient på omkring 1,5 – 2 W·m^-1·K^-1.

7.5 Øvrige parametre

Densitet og varmekapacitet for jordpartikler varierer kun meget lidt mellem forskellige jordtyper /9/, og der er ingen grund til at forsøge at bestemme disse. For ren kvartssand sættes densiteten til 2650 kg·m^-3 og varmekapaciteten er 840 J·kg^-1·K^-1, og disse værdier kan benyttes som standardværdier.

Porøsiteten varierer inden for et forholdsvis snævert interval, og den har ikke stor betydning for selve opvarmningen. For sand vil den typisk være 0,4.

Vandindholdet i dampzonen benyttes til at beregne den overordnede varmekapacitet for jorden, idet vand, der ikke fortrænges, nødvendigvis skal opvarmes sammen med jordpartiklerne til damptemperatur. Derudover indgår værdien i bestemmelsen af den luftfyldte porøsitet, som benyttes, når opvarmningen ved varmeledning overstiger konvektionen. Trykket i dampzonen er uafhængigt af vandindholdet, eftersom det altid antages at være i steady-state.

Vandindholdet skal angives i mætning, hvilket vil sige den del af porøsiteten, der optages af vand. I en given sandtype kan vandindholdet i dampzonen findes ud fra en retentionskurve og kapillartrykket, der angiver trykforskellen mellem dampfasen og vandfasen. Da damptrykket altid er forholdsvist højt, vil vandmætningen være tæt på residualmætningen. For de sandtyper, hvor permeabiliteten er høj nok til, at dampinjektion er relevant, vil en værdi omkring 0,2 i de fleste tilfælde være repræsentativ. Det kan ikke anbefales at bestemme en retentionskurve udelukkende med det formål at bestemme vandindholdet i dampzonen.

Fælles for de ovennævnte øvrige jordparametre er, at de kun har indflydelse på den tid, det tager for en given dampzone at udvikle sig. De har således ikke betydning for dampzones form eller injektionstrykket, og det vil ikke have den store praktiske betydning, hvis de er behæftede med usikkerhed. Det er ikke afgørende om det tager syv eller otte dage for en dampzone at udvikle sig, men det kan være afgørende, om den når syv eller otte meter ud fra injektionsboringen.

Radius af injektionsboring har betydning for beregningen af trykket i boringen, og er derfor kun relevant i tilfælde, hvor injektionstrykket er begrænsende. Hvis filtermaterialet rundt om filteret har en permeabilitet, der er svarer til formationens, bør man sætte filterets radius ind og ikke boringens radius.

På siden standarddata kan der yderligere stilles på en række parametre under overskriften avanceret. Her angives en række beregningstekniske parametre, som det normalt ikke er nødvendigt at ændre. I feltet no-flow angives om jordoverfladen, som er øvre grænsebetingelse, skal være en no-flow grænse eller have fastholdt tryk og temperatur. I praksis vil det næppe være realistisk nogensinde at lade dampen strømme op gennem jordoverfladen, så hvis ikke overfladen er befæstet stoppes dampinjektionen inden dette sker. Derfor kan man som hovedregel altid benytte sig af en no-flow grænse.

Konvergenskriteriet kan benyttes til at variere kravet til, hvornår tryk-beregningen er tæt nok på steady-state. Hvis det sænkes vil beregningen blive mere nøjagtig, men vil tage længere tid. Når konvergenskriteriet er 1, er beregningen så tæt på steady-state, at de øvrige bidrag til usikkerheden er klart dominerende.

Tidsskridtkriteriet kan benyttes til at variere tidsskridtet i temperaturberegningen. Det kan være nødvendigt i nogle tilfælde med meget høj injektionsrate at sænke tidsskridtet, men i så fald vil modellen selv give besked om det. Ligeledes kan tidsskridtet hæves, hvis man simulerer meget lange injektionsperioder med meget lav injektionsrate.

Diskretisering kan ændres alt efter, om man vil optimere nøjagtigheden eller hastigheden. Det kan anbefales at mindske diskretiseringen, når man er nået frem til afgørende simulering for at se om det har nogen betydning. I de fleste tilfælde vil den nøjagtighed, der opnås med diskretisering på 0,3 m, være fuldt ud tilfredsstillende.

Maksimal dybde benyttes til at bestemme størrelsen af modellens beregningsområde. Hvis det forventes, at temperaturen vil være påvirket dybere end 8 m under nederste filter, skal værdien øges.

Regnearket er formateret til en skærmopløsning på 1024x760, hvilket er den opløsning de fleste nyere skærme benytter. Hvis man kun benytter en opløsning på 800x600 skal man markere feltet skærmopløsning 800x600. Skærmopløsningen har kun betydning for figurerne og udprintningen af disse. Hvis der benyttes andre opløsninger, kan man manuelt formatere figurerne inden de printes.