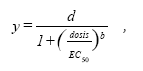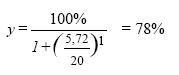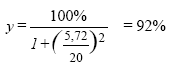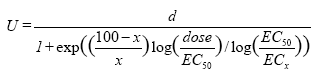|
Pesticiders påvirkning af planter og alger i vandmiljøet 7 Kombinationseffekter
Resultaterne indtil videre har vist, at ingen af de i Danmark målte herbicider i søer og vandløb optræder i koncentrationer, der kan betragtes at udgøre en risiko for vandplanter og alger. Undtagelsen var terbuthylazin, men da de højeste og potentielt væksthæmmende koncentrationer formodes at forekomme i pulse, som for terbuthylazins vedkommende har en meget lille effekt, er det heller ikke sandsynligt, at målte terbuthylazin-koncentrationer vil påvirke den akvatiske flora radikalt. Herbicider og andre potentielt væksthæmmende stoffer findes imidlertid sjældent enkeltvis (Løkke, 2000). Ud af de 140 NOVA-prøver, hvor der blev målt pesticider i koncentrationer over detektionsgrænsen, var der mere end 7 stoffer tilstede i over halvdelen af prøverne. Amerikanske undersøgelser af over 80 stoffer i overfladevand viste tilsvarende resultater (Martin et al., 2003). I Fyns Amt blev der målt op til 18 forskellige stoffer på et døgn (Løkke, 2000). Så hvad er effekten af tilstedeværelsen af flere stoffer på en gang? Og findes der metoder, hvormed man kan estimere effekten af flere stoffer, hvis man kender koncentrationerne af de enkelte? 7.1 Hvad ved vi om kombinationseffekterSelvom problematikken har været kendt længe, er gode systematiske undersøgelser af kombinationseffekter af pesticider i miljøet først for alvor dukket op i løbet af de sidste 10 til 20 år. Der er mange "skoler" og forskellige teorier og terminologier, som er godt opsummeret i reviews (Altenburger et al., 2003; Greco et al., 1995; Berenbaum, 1989). I store træk kan det koges ned til to modeller: 1) Addition af koncentrationer (Concentration Addition, CA, også kaldet Additive Dose Model. ADM) og 2) Uafhængig virkning (Independent Action, IA også kaldet multiplicative survival model (MSM)). CA forudsætter, at de stoffer man regner på, har samme virkemåde. IA forudsætter, at de virker på forskellige mål i organismen. Begge modeller har vist sig at kunne bruges til at beregne effekten af blandinger, hvor mange stoffer er tilstede i meget lave koncentrationer (Faust et al., 2001; Faust et al., 2003; Walter et al., 2002) EC1 har været anvendt for at vise, at selv koncentrationer, hvis effekt vil være umulig at måle, hvis stofferne var testet enkeltvis, har en effekt samlet set. Hvis man sammenligner de to modeller finder man, af CA som regel forudsiger en større effekt end IA. Man finder også, at selv om den teoretiske baggrund bag modellerne er forskellig, vil man sjældent finde en større forskel end en faktor 4 mellem forudsigelserne af de to (Faust & Scholze, 2004). Set i en regulatorisk sammenhæng, hvor man under alle omstændigheder vil benytte sig af en sikkerhedsfaktor på 10, er en faktor 4 lille og mere af akademisk interesse. Og da CA som regel altid vil forudsige en effekt, der er større end effekten forudset med IA, kan man for at være på den sikre side bruge CA som et redskab til at vurdere den mulige maksimale effekt af en blanding. Vi vil i det følgende afsnit beskrive den additive model og v.h.a. et eksempel vise, hvordan den kan bruges til at beregne effekten af en blanding. Eksemplet kan også findes i Cedergreen et al. (2003a). 7.2 Den additive modelVirkningen af et stof på en organisme afhænger af dosis, og i langt de fleste tilfælde kan denne sammenhæng beskrives tilfredsstillende med en logistisk doseringsmodel, som beskrevet i afsnit 2.2.1. og hos Streibig et al. (1993). Kender man et stofs doseringskurve overfor en bestemt organisme, kan man beregne virkningen af en hvilken som helst koncentration af stoffet overfor den givne organisme. Når man bruger den additive model (Additive Dose Model også kaldet Concentration Addition), lægger man doserne eller koncentrationerne af de forskellige stoffer sammen, efter at man har korrigeret dem i forhold til deres relative styrker, hvorefter man beregner virkningen af hele blandingen. Man kan sige, at man omregner doserne/koncentrationerne af pesticider til samme "valuta", hvor vekselkursen bestemmes af forholdet mellem deres giftighed angivet ved deres EC50-værdi. EC50 værdier for en lang række stoffer kan hentes i databaser og opslagsværker (Cedergreen et al., 2003a). Når man har "vekslet" de forskellige koncentrationer af pesticider i en blanding til samme "valuta", lægger man dem sammen og udregner den samlede virkning ved brug af den logistiske doseringsmodel:
Hvor d er den maximale respons (vækst, overlevelse, fertilitet etc.), EC50 er den dosis der giver 50% af den maximale respons og b er proportional med hældningen på kurven i EC50. I beregningen sætter vi den maximale respons, d, til 100%, og anvender den EC50, man har brugt som sin "valuta". Derefter mangler vi bare kurvens hældningsparameter, b, for at kunne beregne virkningen af summen af stofferne. For herbiciders virkning på både alger, vand- og landplanter varierer b som regel mellem 1 og 3 (Cedergreen et al., 2003a). Da de koncentrationer, vi vil beregne virkningen af i en miljømæsig sammenhæng, som regel er lavere end EC50, er det stoffer med en lav b, der vil have den største virkning, hvis de har den samme EC50. Hvis vi derfor antager, at b er lig 1 i de tilfælde, hvor vi ikke har kendskab til den målte b, får vi et konservativt estimat for virkningen af et stof ved koncentrationer < EC50. Tyske undersøgelser med algetests af over 106 forskellige kemiske stoffer viser, at b-værdier <1 findes for mindre end 20% af stofferne (Faust & Scholze, 2004). 7.2.1 BeregningFor at give et eksempel, hvor man kunne have mistanke om en væsentlig miljøpåvirkning, har vi valgt et datasæt, hvor DHI og DMU i forbindelse med en afstrømningshændelse har målt koncentrationer af terbuthylazin, diuron og atrazin på op til henholdsvis 4; 1,8 og 0,5 μg/L (Styczen et al., 2003). Vi finder EC50 værdierne for atrazin og terbuthylazin målt på algen Pseudokirchneriella subcapitata, som er opgivet til at være henholdsvis 45 g/L og ca. 20 μg/L (Tomlin, 2002). For diuron findes der data på algen Chlorella pyrenoidosa, hvor EC50 er opgivet til at være 24 μg/L (Miljøstyrelsen, pers. comm.). På baggrund af EC50 værdierne beregnes den relative styrke af de målte herbicidkoncentrationer og koncentrationerne lægges sammen (Tabel 10): Tabel 10. Toksikologiske parametre og udregning af den relative toksisitet for de målte herbicider.
Dernæst beregnes algernes relative vækstrate, når de udsættes for det, der svarer til en terbuthylazin koncentration på 5,72 g/L og under antagelsen af, at hældningsparameteren på dosis-responskurven er 1:
En beregnet vækst på 78% betyder, at den pågældende blanding af terbuthylazin, diuron og atrazin maximalt vil kunne hæmme algernes vækst med 22%, hvis kurverne har en hældningsparameter på 1. Sættes hældningsparameteren derimod til 2, sådan som det er målt i adskillige forsøg med P. supcabitata, får man følgende resultat:
Brugen af en mere realistisk hældningsparameter sænker altså den potentielle væksthæmmende virkning fra 22% til 8%. Denne blanding ligger altså på grænsen af, hvad der kunne være kritisk. Da de målte koncentrationer er pulskoncentrationer og herbiciderne fotosyntesehæmmere, er det dog usandsynligt, at denne blanding alene vil have en stor effekt på floraen (j.f. Kapitel 6). Eksemplet viser, at det er muligt, på en forholdsvis enkel måde, at estimere den maximalt mulige virkning af en pesticid-blanding på forskellige organisme-grupper, hvis der findes toksikologiske data på enkeltstofferne. Dette estimat kan så bruges i en samlet vurdering af, om denne blanding kan have en signifikant miljømæssig virkning, og til identifikation af hvilke undersøgelser det vil være relevante at fortage for at belyse en sådan mulig virkning. 7.3 Metsulfuron-methyl og terbuthylazinDa vi i dette studie har koncentreret os meget om metsulfuron og terbuthylazin, har vi lavet et binært blandingsforsøg med disse to herbicider. 7.3.1 Materiale og MetoderDe to testsystemer med Lemna og alger beskrevet i afnit 2.1.1. og 2.1.2. blev anvendt. Herbicider blandes i forholdene: 0:100, 17:83, 33:67, 50:50, 67:33, 83:17, 100:0 relative doser, hvilket i praksis vil sige, at der blev lavet to stamopløsninger på en faktor 10 gange stoffets EC50. Disse opløsninger blev blandet med 17 ml af det ene stof plus 83 ml af det andet etc.etc. Hver blanding blev derefter fortyndet med en faktor 2 i alt 7 gange. Dette gav 7 dosis-responskurver med hver 8 fortyndinger, samt kontrol. Lemna forsøgene blev udført med 3 replika og 12 kontrol, alge forsøgene med 2 replika og 10 kontrol. Efter forsøgets udførelse blev hver af de 7 dosis-responskurver beskrevet med en logistisk dosis-responsmodel, der inkluderer både ECx og EC50 (Streibig et al., 1995):
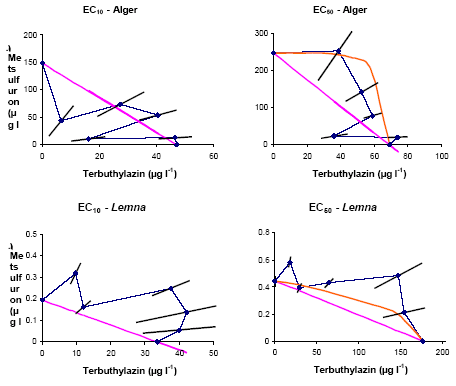
Vi valgte ECx niveauet til EC10. De fittede EC10 og EC50 værdier blev omregnet til koncentrationer af de to enkeltstoffer ud fra kendskabet til deres respektive andel i de forskellige blandinger. Variansen på den fittede værdi blev fordelt proportionalt med andelen af stof i blandingen. Disse koncentrationer blev indtegnet som funktion af hinanden, hvilket giver det, der kaldes et isobologram (Gessner, 1995). Gessner har i en artikel i tidsskriftet Toxicology givet en udmærket illustration af, hvad det er, et isobologram viser (Figur 19a). Det skal dog i den sammenhæng bemærkes, at skalaen på x- og y-akserne skal være logaritmisk, hvis formen på dosis-responskurverne skal være sigmoid. Men princippet er det samme, uanset skala. Figur 19a. En konceptuel model af et isobologram. a) viser en dosis-responskurve for stof 1, samt en dosis-responskurve for en 1:4 blanding af stof 1 og stof 2. b) viser dosis responskurver for stof 1 og stof 2, samt af blandinger af de to stoffer. c) Her er dosis-respons-fladen illustreret ved at forbinde punkter af blandinger, der giver den samme effekt. Kurverne er forbundet med deres projektion på x-y planet. Dette er analogt til højdekurverne på et kort. d) z-aksen er fjernet og et isobologram med kurver for 4 effektniveauer er tilbage. Figuren er lånt fra Gessner (1995). 7.3.2 Resultater og DiskussionIsobolerne for både EC10 og EC50 er vist i figur 19b. Hvis punkterne havde ligget på den rette linie, der forbinder de to enkeltstoffer, havde de fulgt modellen for koncentrations addition (CA). EC50 værdierne for størstedelen af blandingerne er imidlertid større end den forudset v.h.a. modellen for CA. Dette betyder, at blandingerne generelt er mindre giftige end forventet. Da metsulfuron-methyl og terbuthylazin er herbicider med to forskellige virkemåder, ville man forvente, at de fulgte modellen for uafhængig virkning. Denne model er indtegnet som den buede isobol på EC50-figurerne. I dette tilfælde adskiller IA sig ikke særskilt fra CA, og hvis man inddrager usikkerhederne på parameterestimaterne og på estimaterne af isobolerne, er det ikke muligt at sige, hvilke af de to modeller, der statistisk set passer bedst. En additiv eller mindre end additiv virkning er imidlertid et resultat som ofte ses (Christensen et al., 2001; Faust & Scholze, 2004; Faust et al., 1994). Synergistiske effekter på vandplanter og alger er utroligt sjælne, og det har ikke været os muligt at finde et eneste veldokumenteret eksempel (Faust & Scholze, 2004; Kloepper-Sams et al., 2001). På den baggrund og med baggrund i et større EU-projekt, der har indraget data for flere hundrede stoffer testet i forskellige testsystemer på både alger og dyr, er det konkluderet, at CA er en konservativ model, der kan forudsige effekter af blandinger indenfor en sikkerheds-faktor på 5-10 (Faust & Scholze, 2004).
Figur 19b. Isoboler for EC10 og EC50 på blandingen: metsulfuron-methyl og terbuthylazin for både alger og Lemna. Den rette linie mellem de to datapunkter på akserne udgør isobolen for CA, mens den buede linie på EC50 isobolerne udgør IA-isobolen. Punkterne er fittede værdier asymptotisk stdev. En anden konklusion, der kan drages ud fra figurerne er, at isobolerne for EC10 og EC50 er tilnærmelsesvis ens. D.v.s. at de interaktioner vi finder ved de høje koncentrationer der skal til for at nå EC50 også, i dette tilfælde, gælder for de lavere, mere miljørelevante koncentrationer. Det er også i andre forsøg vist, at modellerne CA og IA kan anvendes på blandinger med stoffer i koncentrationer, der giver meget lave effektniveauer (Faust et al., 2001; Faust et al., 2003; Junghans et al., 2003). Der er sammenfald mellem Lemna- og alge-testen, hvilket bekræfer den mindre end additive respons' generalitet på tværs af arter.
|