| Forside | | Indhold | | Forrige | | Næste |

Pesticider i dansk grundvand - Grumo- og boringskontroldata

Bilag A

Principal Component Analyse (PCA) og klassificering

De forskellige datasæt er blevet underkastet en såkaldt Principal Component Analyse (PCA), med henblik på dels at studere sammenhænge mellem variable (data), og dels med henblik på at undersøge, hvorvidt boringer med fund af de forskellige pesticider adskiller sig systematisk, og på hvilken måde, fra boringer uden fund. De anvendte variable er hovedkomponenter indlæst i GEUS database Jupiter. Pesticidindholdet har således udelukkende været anvendt til udvælgelse af boringer. Den anvendte metode falder indenfor disciplinen kemometri. Kemometrien er vel etableret og vel beskrevet, men især to kilder har været anvendt i det følgende:

- Brereton, 1992, Multivariate pattern recognition in chemometrics, illustrated by case stories

- Wise Barry M. And Galagher Neal B., 1998, PLS toolbox tutorial.

I det følgende bliver der brugt betegnelserne variable om de data der er opnået på prøverne og objekter om prøverne.

1.1 Værktøjer

Den kemometriske undersøgelse er udført på standard PC med programmerne Matlab version 6.5 (release 13) fra Mathworks inc., med tilføjelsesprogrammet PLS_Toolbox version 3.0 fra Eigenvector Research inc.

1.2 Princip

PCA bruger princippet om at finde kombinationer af variable (faktorer eller såkaldte latente variable) til at beskrive tendenserne i datasættet. Normalt er variable ikke uafhængige og målet er med så få såkaldt latente variable at beskrive den systematiske variation i datasættet. Det svarer lidt til at man i et bivariat datasæt forsøger at lave lineær regression. Ved at gøre dette reducerer man antallet af variable fra to til en. Denne ene variabel er således en latent variabel, der ikke i sig selv kan oversættes til en bestemt egenskab, idet den er en linear kombination af de to variable. Den algoritme man anvender, mindste kvadraters metoder, sikrer at der er mindst mulig fejl på forudsigelserne lavet på modellen (regressionslinien).

I et multivariat tilfælde er det lidt mere kompliceret. Først finder man den retning i objekt rummet, det vil sige det rum hvori objekterne (prøverne) afbildes, der forklarer størst mulig af datasættets variation. Hernæst fortsætter man med en ny retning, idet det kræves at næste retning er orthogonal (det vil sige vinkelret) på den første, samtidigt med at man tilstræber at mest muligt variation i den resterende matrice forklares. Denne forudsætning sikrer at de latente variable, i modsætning til de reelle variable, er uafhængige. Korrelationen mellem to orthogonale vektorer er nul. Man har en række metoder til at vurdere antallet af latente variable der skal ekstraheres, dels kan man bruge sin sunde fornuft og vurdere residualet i forhold til målesikkerhed, og dels kan man se på modellens evne til at prediktere hver enkelt objekt for hver iteration i forhold til den foregående. Falder modellen prediktive evne, har man taget for mange latente variable med og man stopper med at ekstrahere flere komponenter.

Matematisk kan problemstillingen udtrykkes på følgende måde:

X = t₁p^T₁ + t₂p^T₂ + t₃p^T₃ +.........+ t_'np^T_n + E (1)

X er den originale datamatrice. Vektorerne tn er såkaldte loading vektorer der indeholder information om, hvordan de enkelte variable relaterer sig til hinanden. Vektorerne p_n er såkaldte score vektorer, svarende til de latente variable der er omtalt ovenfor. T angiver at vektoren er transponeret hvilket betyder at der byttes om på rækker og søjler. Når en vektor transponeres ændres den fra en søjle vektor til en række vektor. Som det fremgår af ovenstående er matricen X opløst i en linear kombination af matricer der er opnået ved at multiplicere loading vektorer og transponerede score vektorer. Man kan således repræsentere de enkelte variable i den originale matrice i et rum udspændt af loading vektorerne eller objekterne i den originale matrice i et rum udspændt af score vektorerne. Matricen E angiver residual matricen, eller fejlen på modellen i forhold til det originale data sæt (X).

Loading vektorerne udregnes ud fra covarians matricen på X :

Cov(X)=X^TX/(m-1) (2)

Hvor m er lig med antallet af variable i datasættet. Loading vektor, for i'te iteration, findes som eigenvektoren til covarians matricen på X idet:

Cov(X)p_i = _ip_i (3)

Her er _i eigenværdien for den pågælden eigenvektor p_i (loading vektoren for i'te iteration).

Den tilsvarende score vektor t_i findes ud fra formlen:

Xp_i = t_i (4)

Score vektorerne er orthogonale, på samme måde som loading vektorerne der desuden er orthonormale (længden 1) og t_i kan forstås som den originale matrices projektion på den tilhørende loadingvektor p_i.

Da eigenværdierne har den egenskab, at den første er den største, og at de derefter falder i værdi, opfylder loadingvektorerne og dermed scorevektorerne den egenskab at de tilsammen indeholder en faldende mængde information om datamatricen, efterhånden som iterationen skrider frem. Oplever man at eigenværdier stiger mellem to iterationer, tyder dette ofte på at datasættet indeholder flere klasser, eller at man modellerer på støjen i data sættet, hvilket kan bruges aktivt. Der findes desuden en række valideringsprincipper så kun signifikante komponenter ekstraheres fra datasættet.

Da score vektorer og loading vektorer er orthogonale, og dermed uafhængige, kan almindelige statistiske overvejelser anvendes på disse, f.eks. kan der findes konfidensintervaller ved hjælp af normalfordelingen. Dette betyder at man kan finde outliers blandt objekterne og blandt de enkelte variable ved simple statistiske overvejelser. En anden måde at identificere outliers på er ved at vurdere objekternes eller de enkelte variables bidrag til residual matricen. Disse to principper finder anvendelse ved vurdering af hvorvidt objekter hører til en bestemt klasse.

Figur 1 viser princippet i PCA. Et tredimensionalt datasæt kan repræsenteres i to dimensioner ved hjælp af PCA analysen. Ellipsen illustrerer konfidensintervallet i planet udspændt af de to principal komponenter. Der vises to prøver der hver for sig illustrerer en outlier. Den ene prøve er karakteriseret ved at ligge i planet, men have en variation der er udenfor konfidensintervallet (large T²). Dette svarer i tilfældet med lineær regression til at punktet ligger på regressionslinien men langt fra de punkter modellen er bygget over. Den anden prøve vil projiceret på planet ligge indenfor konfidensintervallet, men har en stor residual værdi (large Q). I tilfældet med lineær regression svarer det til et punkt der ligger langt fra regressionslinien.

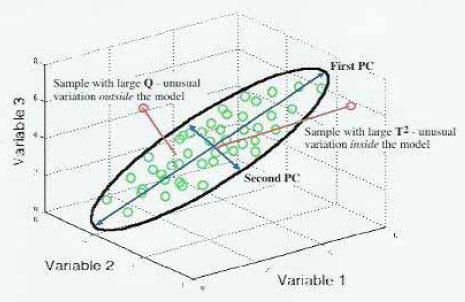
Figur 1. Illustration af PCA taget fra Wise and Gallagher

1.3 Grafiske fremstillinger anvendt i analysen

Der er brugt en række grafiske fremstillinger i forbindelse med den kemometriske behandling af data.

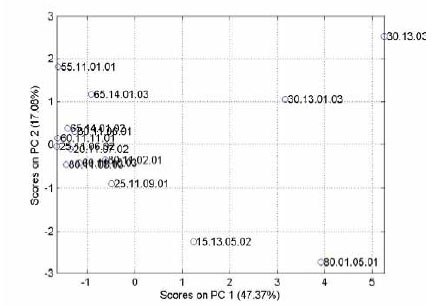
Figur 2. Score plot

Figur 2 viser et såkaldt score plot, altså en projektion af objekterne på det reducerede variabel sæt. I dette tilfælde er der 5 signifikante principal komponenter (her vises dog kun de to), og man skal være opmærksom på at der er variationer i andre dimensioner end de der fremgår af det to dimensionale plot. Som det fremgår bærer første principale komponent godt 48% af variationen i data sættet og er altså den vigtigste, mens principal komponent 2 bærer godt 17%. Man kan i score plottet studere sammenhængen mellem objekterne, jo tættere de liggere, des mere lig er de. I dette som i alle andre plots der vil blive vist, er korrelationen mellem to objekter (eller variable senere), projektionen af den vektor der går fra (0,0) til det ene punkt på den vektor der går fra (0,0) til det andet punkt (i de viste dimensionen !). Er vinklen mellem de to vektorer nul, er objekterne eller de enkelte variable uafhængige. Tager man f.eks. nedenstående loading plot (figur 3), og vil estimere korrelationen mellem ilt (O₂) og metan (CH₄), trækker man en linie mellem punktet (0,0) og punktet O₂ samt mellem (0,0) og punktet CH₄. Korrelationen er da projektionen af den ene linie på den anden. Des tættere vinklen mellem linierne er på 90 grader, des lavere bliver korrelationen.

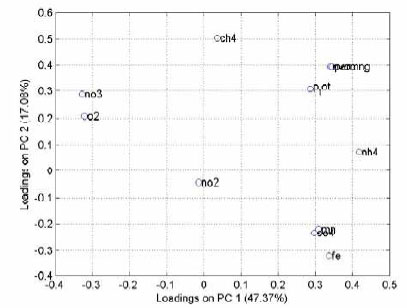
Figur 3. Loading plot

Figur 3, loading plottet, viser sammenhængen mellem de enkelte variable projiceret på de samme to principal komponenter som i figur 2. Figur 3 angiver sammenhængen mellem de enkelte variable i de to dimensioner, og kan også bruges til at vurdere hvilken information principal komponenterne hovedsageligt bærer. I ovenfor viste tilfælde er dette imidlertid vanskeligt.

I figur 4 er vist det såkaldte biplot hvor både variable og objekter er projiceret ind på de samme to principal komponenter, hvilket svarer til at man lægger figur 2 og figur 3 oven på hinanden. Biplottet kan bruges til at se hvorfor nogle objekter er outliers eller hvad der er den underliggende årsag til at objekterne ligner hinanden. Prøve no. 80.01.05.01 kunne f.eks. være langt fra de andre på grund af højt indhold af jern og sulfat, men det kunne også være lavt indhold af nitrat og ilt (formentligt begge dele). Ovennævnte prøve ligger tæt på gruppen af jern og sulfat (røde triangler, Fe og SO₄) og langt fra gruppen af nitrat og ilt (røde triangler, O₂ og NO₃).

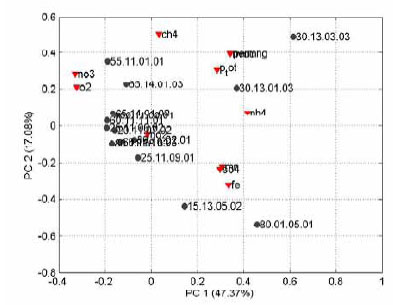
Figur 4. Biplot

Når man har dannet en god model af en række objekter (boringer med fund), kan det være relevant at undersøge om nye prøver, eller prøver fra en anden population (boringer uden fund) passer ind i modellen, og hvis ikke hvorfor de ikke gør dette. Her kan man bruge biplottet fra figur 4 og projicere de nye prøver ind på dette som vist i figur5.

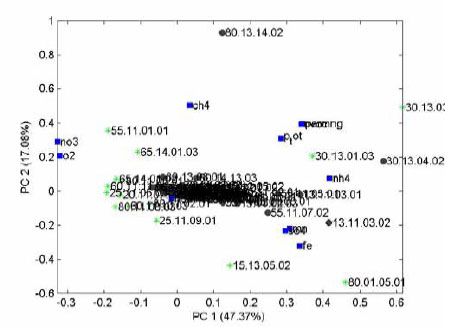
Figur 5. Biplot med projicerede data

De grønne markeringer viser de objekter der har dannet modellen (boringer med fund), mens de sorte unavngivne viser de projicerede data (boringer uden fund). De blå kvadrater angiver beliggenheden af de enkelte variable. I dette tilfælde er det nærliggende at tolke de nye objekter (boringer uden fund) som generelt lave i nitrat og ilt, og høje i jern, sulfat og ammonium. Da der kan være en stor residual værdi for disse prøver er det imidlertid nødvendigt at checke rå data for at få dette bekræftet.

| Forside | | Indhold | | Forrige | | Næste | | Top |

Version 1.0 September 2005, © Miljøstyrelsen.