Erfaringsopsamling på udbredelsen af forureningsfaner i grundvand på villatanksager
Bilag D: Databehandling
I det følgende gennemgås databehandlingen der ligger til grund for konklusionerne i nærværende rapport. Der er udført forskellige dataanalyser for undersøgelse af henholdsvis fanelængde samt til vurdering af en eventuel øget udvaskning ved relativt højere vandspejl.
Fanelængde
For at få en struktureret og kvantitativ databearbejdning, er der for hver dataanalyse i rapportens afsnit 2, optegnet følgende plots:
Plot A: Empirisk fordelingsplot af fanelængde.
Plot B: Relativ fanelængde (L/Lmax) som funktion af tid efter spildtidspunkt/afværgeafslutning med 50 % fraktil plottet som funktion af tiden.
Plot A
I det følgende er den statistiske procedure, der ligger til grund for det empiriske fordelingsplot for de opmålte fanelængder beskrevet – via et eksempel baseret på opmålte fanelængder (>9 µg/L) fra alle sager.
Indledningsvist er fanelængder rangeret og plottet mod den empiriske fordelingsfunktion /4/:
![]()
Hvor i er nummeret på observationen, efter rangordning, N er antallet af observationer og FN(X) er den empiriske fordelingsfunktion; dvs. den fraktion af data der er mindre end eller lig med værdien for observation nr. i.
Af figur D.1 fremgår eksemplet på den empiriske fordelingsfunktion.
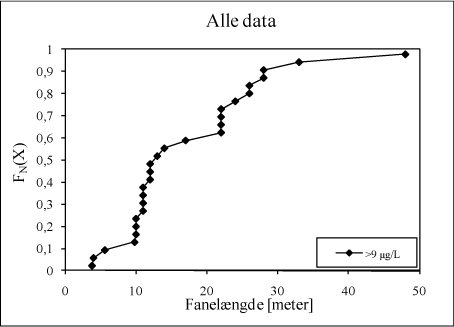
Figur D.1. Empirisk fordelingsfunktion for fanelængder (alle data).
Plot B
Til vurdering af den tidslige udvikling af fanelængden, er der for at undgå subjektivitet i datatolkningen opstillet en standardiseret metodik til fraktilestimering, som er ”programmeret” i Excel og som beskrives i det følgende. De rå data som beskriver den tidslige udvikling er plottet som det fremgår af figur D.2.
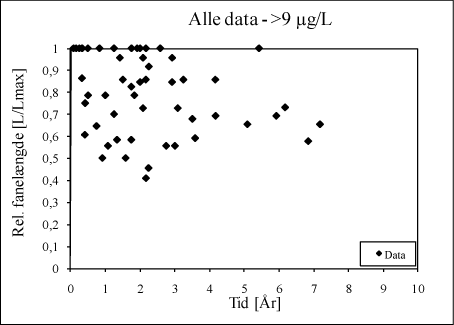
Figur D.2. Tidslig udvikling i fanelængde efter spild-/afværgetidspunkt.
Havde data været målt på ”pæne/ordnede” tidspunkter; f.eks. efter 1, 2 og 3 år osv. ville man til hvert tidspunkt kunne estimere fraktiler ved en simpel rangordning af koncentrationsdataene til hvert tidspunkt. Var der f.eks. 10 datapunkter målt til tiden 1 år efter spildtidspunkt/afværgeafslutning, ville 50 % fraktilet eksempelvis kunne estimeres som mellemste fanelængde.
Nu er data imidlertid ikke målt på ordnede tidspunkter, hvorfor der er foretaget en tidsmæssig gruppering af de målte data, således, at det indenfor hver tidsmæssig gruppering er muligt, at estimere fraktiler, som om data indenfor hver gruppering var målt til samme tidspunkt. Dette er essentielt en form for numerisk statistik.
Hver gruppering er som udgangspunkt valgt således, at der er mindst 2 datapunkter repræsenteret i hver gruppe. Desuden er grænserne forsøgt valgt således, at de (efterfølgende) estimerede fraktiler ikke misrepræsenterer data i scatterplottet (figur D.2). For data i figur D.2 kommer gruppeinddelingen til at se ud som i figur D.3.
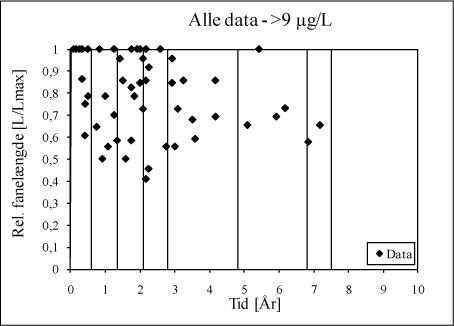
Figur D.3. Gruppeinddelinger af data, til estimering af fraktiler indenfor hver gruppe.
Efterfølgende er fraktilfunktionen i Excel benyttet til at estimere 50 % fraktiler for hver gruppe; svarende til den koncentration, som halvdelen af data (mindst ét datapunkt) er lavere end. Fraktilestimatet for hver gruppe er efterfølgende tilegnet den tidslige middelværdi i hver gruppe – og der er optegnet linjer imellem estimaterne for hver datagruppering.
Det endelige resultat er vist i figur D.4.
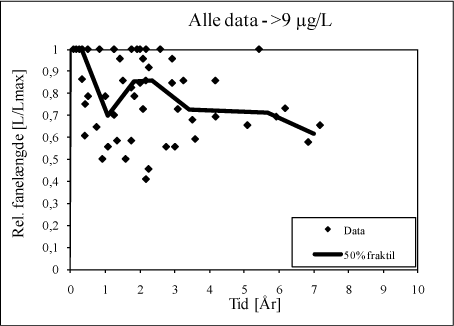
Figur D.4. Endelig præsentation af 50 % fraktilestimater for de opmålte fanelængder.
Som det fremgår af plottet, ”fanger” metoden tendenserne i datamaterialet og det giver mulighed for en kvantitativ tolkning, af mediantendensen for datamaterialet (50 % fraktilet).
Version 1.0 December 2009, © Miljøstyrelsen.