Miljøprojekt, 1011 – Systematisk kontakteksem over for nikkel ved oral eksponering

Systemisk kontakteksem over for nikkel ved oral eksponering

Bilag C

APPENDIKS 1.

The logistic dose-response model used in the analyses describes the probability p(x) of a positive response in a single patient exposed to the Ni- dose x as:

p(x) =1/[1+exp(-α-βlog(x))]

α and β are the parameters of the dose-response model. The parameter β is denoted the slope of the dose-response curve, since it is proportional to the slope of the steepest part of the sigmoid dose-response curve. is denoted the constant or position parameter of the dose-response curve. However, the so-called median effective dose ED₅₀ is normally used to characterize the dose response curve in aδition to β. ED₅₀ is the dose that corresponds to p(x) = 0.5 or the dose that will elicit a positive response in 50 % of the population, and it is calculated as ED₅₀ = exp(α/β). If log(p(x)/(1-p(x)) is plotted against log(x) a straight line is obtained. For this reason the above dose-response model is also denoted the linear logistic model.

The number of patients y with positive response in a group of n patients tested with the same dose x is assumed to follow a binomial distribution with parameter p(x). With data from two or more separate (independent) groups of patients tested with different doses of Ni it is possible to estimate α and β, provided not all response rates (y/n) are equal and at least two are different and greater than 0 and smaller than 1. In that case it is also possible to test the significance of the dose-response dependence, i.e. the null hypothesis: β = 0. Furthermore with three or more intermediate response rates > 0 and < 1 it is also possible to test the goodness fit of the logistic dose-response model.

The so-called multiple logistic regression analysis extends the logistic dose-response to allow a simultaneous analysis of several dose-response relations. With dose-response data from k studies the multiple logistic model may be defined as:

p(x₁, ..., x_k) = 1/exp(-α-β₁log(x₁)- ...-β_klog(x_k))

This model allows different slopes for each dose variable. Another multiple logistic model is:

p(x₁, ..., x_k) = 1/exp(-α₁-...-α_k-β(log(x₁)+...+log(x_k)))

This one assumes the same slope but different positions, i.e. parallel dose-response curves. The most general multiple linear logistic model is the one with k different α's and k different β's.

However, in the present analyses it is not possible to apply the most general model, because it requires that individual models can be estimated with the data from each individual study. The model with a common α and different β's is not very plausible since it assumes that all dose-response curves intersect at some dose. Therefore, the only useful model for studying the properties of the dose-response relations in a number of studies seems to be the one with different α's and the same β, i.e. a series of parallel dose-response curves.

By means of the strategy of stepwise-multiple regression analysis it is possible to determine which α's that are significantly different, and which can be assumed equal. The model above is modified to the following:

p(x) = 1/exp(-α-δ₁...-δ_k-δlog(x))

The parameter α now denotes the average of the k individual α's, while the δ's represent the deviations between the average and the individual α's. Thus, by testing nil hypotheses for the δ's it is possible to determine which studies differ from the average. Depending of the outcome of the stepwise analysis that eventually provides the (sub)set of significant δ's, the analysis is continued to determine if some of the significant δ's can be assumed equal, and the analysis is stopped, when no more reduction is possible. From the estimated values of the model parameters: α, β, δ₁, ..., δ_k is it possible to calculate the dose that corresponds to a given value of the probability of positive response or the fraction of patients in the population. Inversion of the dose-response model gives the following equation for calculation of the dose associated with a response rate of 100·p %.

equation for calculation of the dose associated with a response rate of 100·p %

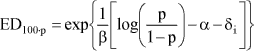
Inserting the estimated values of α, β, δ₁, ..., δ_k enables calculation of the doses corresponding to the chosen value for p for any study group. Moreover, it is possible to determine 95 % limits for ED_100·p by Fieller's method and the asymptotic covariance matrix of the parameter estimates which is obtained from the logistic regression analysis.

The modification of the logistic model in case of a positive background response rate will briefly be outlined. Denoting the probability of a positive response to placebo (or Ni-dose 0) by p₀, the simplest dose-response model may be written as:

p(x) = p₀ + (1p₀)/[1+exp(-α-βlog(x))]

In order to successfully estimate such a dose-response model it is necessary to have relative precise estimates of the response rate at dose zero and at least at two higher doses where the response rates are higher and increase with the dose. The interpretation of the parameters α and β and ED₅₀ will change and depend on the value of p₀. Thus, this model is not very attractive. Table 3.2.2 shows an example of its application in the analysis of the data from study 16.

Finally, it will be pointed out that the above-mentioned dose-response modelling analysis does not apply to the experimental situation where the same group of patients is tested with different doses, incl. dose 0. In this case the responses represent non-independent (correlated) binomial data, and special methods are required. One of these would be to regard the increasing response rate as observations of the tolerance of the patients. This requires the implicit assumption that if a patient has shown a positive reaction to a given dose that person will also show a positive reaction to all higher doses. This may be checked by inspection of the individual responses to the doses in question, but the reported response rates do not contain this information except when none or all patients react. Table 3.2.2 shows an example of estimation of the dose-response relation as a tolerance (logistic) distribution curve based on the data from study 3.