Statistisk analyse og biologisk tolkning af toksicitetsdata
6 Analyse af binomialt respons
Et binomialt respons defineres som en sum af en række uafhængige eksperimenter med kun 2 udfald, 0 eller 1, f.eks. død/levende, ikke-mobil/mobil, aktiv/ikke-aktiv.
6.1 Problemstilling
Skal man tage hensyn til korrelation introduceret via forsøgsdesignet, f.eks. når flere organismer af praktiske hensyn er grupperet eller samlet i en beholder? Med andre ord drejer det sig om analyse af binomialt respons med grupperede data, som er en særdeles udbredt måde at udføre bioassay på. For binomialfordelte responser forudsættes det normalt, at dosis-responsmodellen, dvs. sandsynligheden for positivt respons er 0 for dosis 0, og at den vokser asymptotisk mod 1, når dosis går mod uendelig (eller omvendt). Derfor kan man med standardmetoder få misvisende resultater, hvis man ikke kan benytte mere generelle modeller med nedre responsegrænse > 0 (eller øvre grænse < 1).
I R-pakken drc kan man vælge modeller, hvor såvel nedre som øvre grænse estimeres ud fra data.
6.1.1 Datakilde
Data er resultat af en larveudviklingstest med saltvandskrebsdyret Acartia tonsa. Disse dyr undergår morfologiske ændringer fra en række larvestadier indtil voksenstadierne nås. I larvestadierne benævnes dyrene som nauplier og i voksenstadierne som copepoditter. Der er derfor 2 mulige udfald for hvert dyr, og antal dyr, som efter en given påvirkning er i copepodit-stadiet, kan opfatttes som binomialfordelt (Ole Kusk, ikke publiceret).
Da dyrene i hvert replikat er grupperet i et glas, bør man tage dette i betragtning, fordi den grundlæggende binomialfordelingsmodel bygger på antagelsen om at de enkelte dyr reagerer på stimulus uafhængigt af hinanden, en forudsætning som i dette tilfælde måske er tvivlsom, når larverne lever tæt sammen. Den type korrelation mellem individer vil ofte manifestere sig i form af overspredning, dvs. at der forekommer en større variation i data, end hvad man ville forvente ud fra den valgte model.
6.1.2 Analyse af data
Først betragter vi en model, som antager at der er binomialfordelt respons, som beskrives ved en 2-parameter log-logistisk dosis-respons-kurve med nedre grænse 0 og øvre grænse 1. Bemærk at det her er den log-logistiske model som vist i ligning 2.1 med den forskel at den øvre grænse er fastsat til 1. Mere præcist er modellen for sandsynligheden p(x) for at en larve bliver copepodit ved en bestemt dosis givet ved:
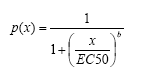 (6.1)
(6.1)
med parametre b og EC50. Parameteren b er proportional med hældning, når dosis er lig EC50. Denne model er identisk med en standard logistisk regressionsmodel med logaritme-transformerede doseringer (det er blot en anden parametrisering som er benyttet):
![]() (6.2)
(6.2)
hvor logit(p) er defineret som log(p/(1-p)). Modellen baseret på Ligning (6.1) antager, at der er sandsynlighed 0 for at blive copepodit til dosis 0, og derfor er kontrolgruppen med dosis 0 overflødig og kan uden problemer udelades. Derfor er det heller ikke noget problem, at Ligning (6.2) ikke er defineret for dosis 0 (x=0). Ud fra modellen fås følgende estimerede EC-værdier med standardfejl i parentes:
EC10 = 0,55 (0,14)
EC50 = 5,83 (0,67)
Pearson’s goodness-of-fit-teststørrelsen (McCullagh & Nelder, 1989, s. 37) har en værdi på 74 og er således særdeles signifikant (p-værdi= 1,3 ·10-7), så modellen giver ikke nogen god beskrivelse af data. Det kan man også se på Figur 6.1 til venstre, fordi der ikke er data der tilsiger, at den øvre grænse, som vist i Ligning (6.1) er 1. Derfor er det naturligt at betragte en model, som antager, at vi har et binomialfordelt respons som beskrives ved en dosis-respons-kurve med nedre grænse 0, men en øvre grænse som skal bestemmes ud fra data. Modellen for sandsynligheden for, at en nauplie udvikles til en copepodit, er:
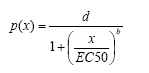 (6.3)
(6.3)
Ligning (6.3) er en tre-parameter log-logistisk model, hvor parameteren d betegner den øvre grænse, mens parametrene b og EC50 har samme fortolkning som i ovenstående 2-parameter model i Ligning (6.1).
Denne model giver følgende estimerede EC-værdier med standardfejl i parentes:
EC10 = 13,60 (2,26)
EC50 = 24,66 (2,57)
Goodness-of-fit-testet er stadigvæk signifikant, dog ikke så meget som før (teststørrelse=69, p-værdi=0,0003). Den estimerede dosis-responskurve kan ses nedenfor i Figur 6.1 til højre. Vi bemærker, at de estimerede EC-værdier ændrer sig ganske meget, de bliver større end i modellen med fast øvre grænse på 1.
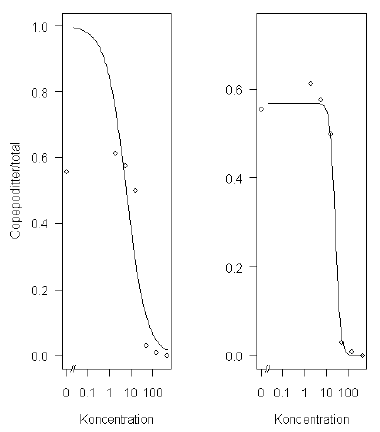
Figur 6.1. Estimerede dosis-responskurver baseret på modeller med og uden estimation af den øvre grænse for Acartia tonsa-datasættet.
Ud fra Figur 6.1 til højre er det tydeligt, at der er en svag stimulering ved lave koncentrationer. Dette betegnes ofte som hormesis, der kan modelleres f.eks. vha. hormesis-modellen introduceret af Cedergreen et al. (2005). Den resulterende estimerede dosis-responskurve er vist i Figur 6.2. Goodness-of-fit-testet er nu heller ikke så signifikant (p-værdi=0,002) som for de tidligere modeller. Rent faktisk viser denne model, at den hormesis effekt ikke er signifikant (p-værdi=0,25), og derfor kan hormesis-modellen reelt reduceres til den log-logistiske model med estimeret øvre grænse (Figur 6.1 til højre).
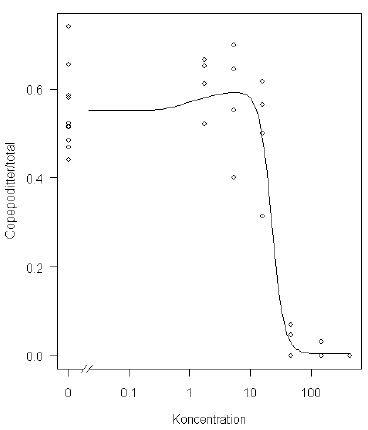
Figur 6.2. Det originale Acartia tonsa-datasæt med en estimeret dosis-responskurve baseret på hormesis-modellen introduceret i Cedergreen et al, (2005). Alle datapunkter er vist.
Hermed har vi fundet en model (den log-logistiske model med estimeret øvre grænse), der beskriver middelværdistrukturen i data på en rimelig, om end ikke helt tilfredsstillende måde. Da individerne i et glas (20-45 pr glas) muligvis påvirker hinanden, er næste skridt at justere for korrelationen mellem dem. Man vil ofte forvente, at der er overspredning, fordi der er mere variation i data end hvad modellen med uafhængighedsantagelsen kan forklare. Den simpleste måde at justere på er ved at gange alle estimerede standardfejl for estimaterne i modellen med en faktor, der afspejler hvor meget overspredning, der er til stede i data. Overspredningsfaktoren udregnes som kvadratroden af værdien af goodness-of-fit-testet, som vi allerede har brugt, divideret med antallet af frihedsgrader (McCullagh & Nelder, 1989, pp. 124-128), dvs. v(69/33)=1,45. Efter denne korrektion bliver resultatet for den log-logistiske model med estimeret øvre grænse:
EC10 = 13,60 (3,27)
EC50 = 24,66 (3,71)
De estimerede EC-værdier er således uændrede, men de tilhørende standardfejl bliver noget større, fordi de nu bedre afspejler den reelle variation, der er til stede i de eksperimentelle data.
6.1.3 Afsluttende bemærkninger
Det kan være problematisk blot at bruge en standard log-logistisk regressionsmodel, som antager nedre grænse 0 og øvre grænse 1, hvor der i virkeligheden ville være brug for at estimere den øvre grænse. Dette har den konsekvens, at EC-værdier kan blive underestimeret.
Anbefaling: Hvis der er tale om et forsøgsdesign, som kunne give anledning til korrelation (dvs. design hvor der er risiko for at organismerne påvirker hinanden), så bør man justere de estimerede standardfejl, så der også tages hensyn til denne ekstra variabilitet i data.
6.2 Analyse af binomialfordelt respons med modeller for kontinuert respons
6.2.1 Problemstilling
I litteraturen ses af og til at binomialfordelte data behandles med statistiske modeller, der forudsætter at data er kontinuerte. Spørgsmålet er derfor, hvor stor en fejl man begår ved at analysere binomialfordelte data vha. en model for kontinuerte data.
6.2.2 Datakilde
Vi benytter doseringer og parameterværdier estimeret baseret på Acartia tonsa-datasættet fra forrige afsnit.
6.2.3 Simulationstudie
Forsøgsvis anvender vi den tilsvarende model for et kontinuert respons, hvor øvre grænse estimeres, mens nedre grænse holdes fast på 0, se Ligning (6.3). Det gøres ved at konvertere binomialdata til procent og dermed betragte dem som kontinuerte data. Dette giver følgende estimerede EC-værdier:
EC10 = 15,14 (2,63)
EC50 = 24,92 (4,88)
Selve estimaterne er ikke voldsomt forskellige fra modellen med binomialfordelt respons (med nedre grænse 0 og øvre grænse 1), men de tilhørende standardfejl ændres betragtelig. I det følgende vil vi undersøge nærmere, hvilken konsekvens det har at betragte binomial respons som om det var kontinuert.
Der blev genereret 1000 datasæt baseret på binomialfordelingen ud fra en to-parameter log-logistisk regressionsmodel med en hældning b på 0,93 og en EC50-værdi på 5,83 og med samme doseringer som i Acartia tonsa-datasættet for hver af de følgende totale antal larver: 10, 20, 30, 40, 50, 60, 100, 500, 1000 og 10000.
For hvert datasæt blev både den korrekte binomiale model (B) og den tilsvarende kontinuerte model (K) tilpasset til data. Resultaterne i form af relativt bias, dvs forholdet mellem forskellen (differensen) fra estimat til den rigtige EC-værdi for den kontinuerte og binomialfordelingsmodellen, og efficiens, dvs. forholdet mellem standardfejlen på estimaterne baseret på den kontinuerte og binomialfordelingsmodellen, er opsummeret i Tabel 6.1.
Tabel 6.1 Sammenligning af relativ Bias og efficiens for EC10 og EC50 ved at antage kontinuert normalfordeling og antage den korrekte binomialfordeling.
| Bias | Efficiens | |||
| Antal dyr per dosis | EC10 | EC50 | EC10 | EC50 |
| 3 | 1,06 | 1,00 | 1,34 | 1,03 |
| 5 | 1,02 | 1,00 | 1,23 | 1,03 |
| 10 | 1,00 | 1,00 | 1,21 | 1,02 |
| 20 | 1,00 | 1,00 | 1,22 | 1,02 |
| 30 | 1,00 | 1,00 | 1,21 | 1,02 |
| 40 | 1,00 | 1,00 | 1,21 | 1,02 |
| 50 | 1,00 | 1,00 | 1,23 | 1,02 |
| 60 | 1,00 | 1,00 | 1,22 | 1,02 |
| 100 | 1,00 | 1,00 | 1,22 | 1,01 |
| 500 | 1,00 | 1,00 | 1,19 | 1,01 |
| 1000 | 1,00 | 1,00 | 1,17 | 1,02 |
| 10000 | 1,00 | 1,00 | 1,21 | 1,01 |
Tabel 6.1 viser, at der ikke er noget nævneværdigt bias i estimaterne fra den kontinuerte model i forhold til binomialfordelingsmodellen. For efficiens giver det samme billede som sammenligningen af analyserne for Acartia tonsa-datasættet gjorde ovenfor, nemlig at parametrene ikke ændredes sig meget (der er ingen bias), mens standardfejlen gør det. Den kontinuerte model producerer for store standardfejl på EC-værdierne. Mest markant er det for EC10 med en efficiens på omkring 1,2, mens der ikke er stor forskel på standardfejlene for EC50. De relative forskelle ændrer sig ikke meget, uanset hvor stort antal larver der bruges. Efficiensen for EC5 (ikke vist i Tabel 4) var på omkring 1,23, og altså lidt højere end for EC10.
6.2.4 Afsluttende bemærkninger
Resultater viser, at uanset hvor stort antal larver der bruges, så vil den kontinuerte model give for store standardfejl på EC10-værdierne. Derimod forringes præcisionen ikke meget, når man kun betragter EC50. Disse resultater viser, at det ikke er korrekt at antage, at en kontinuert model er acceptabel, hvis blot antal larver (generelt: antal organismer) er stort nok. Dermed er vores resultater i modstrid med gængse anbefalinger, som f.eks. fremsat af Environment Canada (2005, s. 84).
Version 1.0 Oktober 2008, © Miljøstyrelsen.