Statistisk analyse og biologisk tolkning af toksicitetsdata
5 Analyse af kontinuert respons
Inden for såvel human- og økotoksikologi udfører man ofte forsøg med et kontinueret respons, f.eks. længde, højde, vægt, absorbans etc. I modsætning til bioassays med binomiale respons som f.eks. målinger af dødelighed, hvor kun to udfald er mulige, f.eks. død/levende og mobil/immobil.
5.1 Variansheterogenitet
5.1.1 Problemstilling
Forudsætningen for at benytte en konventionel regressionsmodel, det være sig lineær eller ikke-lineær, er at vi kan beskrive kurveforløbet og at variationen i responset er konstant uanset responsniveau, og at responsen er normalfordelt. Konstant varians er i praksis kun tilnærmelsesvis opfyldt, især hvis der er store forskelle i responsniveauerne. Hvis variansen ikke er konstant udviser data variansheterogenitet.
Typisk vil parameterestimater og dermed estimerede EC-værdier ikke ændre sig meget, uanset om der tages højde for variansheterogenitet eller ej (Carroll, 2003). Nedenfor vil vi vise, hvorledes man undersøger for variansheterogenitet, og hvad man kan gøre for at afhjælpe den og vise, at ignorering af variansheterogenitet medfører forkert præcision på estimerede EC-værdier?
5.1.2 Datakilde
Vi vil illustrere problemet ved at anvende data fra et forsøg med små planter af Galium aparine, dyrket i potter i drivhus. Planterne blev sprøjtet med herbicidet phenmedipham, enten alene (herefter benævnt Herbicid 1) eller i en blanding med en ester af oliesyre (Herbicid 2). Planterne stod 14 dage i drivhuset efter herbicidbehandlingen, inden tørvægt per potte blev målt (Cabanne et al, 1999).
Først betragter vi en dosis-respons-analyse af datasættet med en fire-parameter log-logistisk model, hvor variansheterogenitet ignoreres. Residualplottet fra modellen uden transformation i Figur 5.1 viser tydeligt, at der er variansheterogenitet. Det vifteformede mønster, hvor spredningen i residualerne er lille ved små prædikterede værdier og stor ved store prædikterede værdier; et typisk billede for denne type data. For at undgå variansheterogenitet kan man enten vægte eller transformere responset. Tidligere var vægtning udbredt (Finney, 1978). Det er vigtigt her at pointere, at vægtning udelukkende drejer sig om at vægte for at opnå varianshomogenitet, og at det ikke ændrer på den funktionelle sammenhæng mellem dosis og respons. En anden måde at klare variansheterogenitet på er at transformere vha. en potens eller en logaritme-funktion. Vi benytter den såkaldte Box-Cox transformation af såvel højre som venstre side af modelligningen (Streibig et al, 1993). Men andre ord, ved at transformere begge sider af regressionsmodellen forbliver parameterestimaterne i den oprindelige skala, og den matematiske relation mellem dosis og respons er uændret. Hvis der forekommer negative værdier af responsen, så giver det ikke mening at transformere med en potens- eller logaritmefunktion. Man kan derimod benytte Box-Cox-transformationen efter at have lagt et passende tal til alle responsværdier; det er dog ikke aktuelt for det datasæt, vi betragter. Desuden har det vist sig, at ved at benytte Box-Cox transformationen på begge sider af modellen, vil der ofte blive justeret for såvel variansheterogenitet som afvigelser fra normalfordeling. Box-Cox-transformationen er en indbygget facilitet i pakken drc. Den optimale Box-Cox-transformation bestemmes ud fra data.
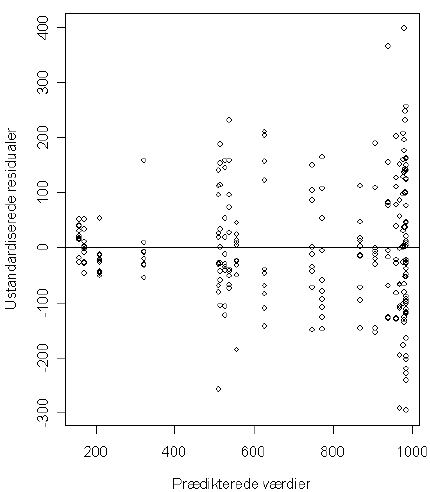
Figur 5.1. Residualplot baseret på model uden transformation.
Benyttes den samme model, men med transformation af både respons og modelfunktion (den optimale transformation er en potensfunktion med eksponent 0,2) fås residualplottet i Figur 5.2.
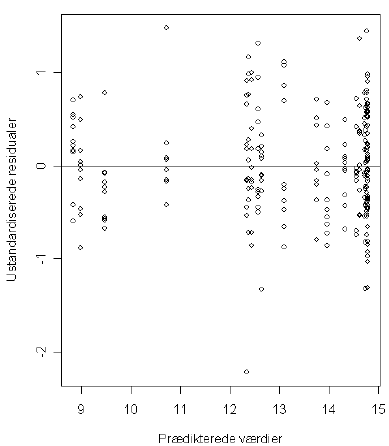
Figur 5.2. Residualplot baseret på model med transformation.
Residualplottet viser ikke længere nogen systematisk vifteform som i Figur 5.1, og vi kan slutte, at modellen med transformationen har medført varianshomogenitet.
Tabel 5.1. EC10 og EC50 estimeret ud fra oprindelige data og transformerede data (Box-Cox-transformation) for to herbicidformuleringer. Standardfejl er angivet i parentes.
| Herbicid 1 | ||
| EC-niveau | Oprindelige data | Transformerede data |
| 10 | 13,82 (4,32) | 13,00 (3,77) |
| 50: | 52,55 (7,61) | 50,82 (7,89) |
| Herbicid 2 | ||
| 10: | 30,74 (4,29) | 26,64 (4,09) |
| 50 | 94,15 (5,74) | 93,43 (8,11) |
For Herbicid 1 ser vi, at ved at anvende transformationen får vi en standardfejl på EC50-estimatet, som er noget større (forøgelse på ca.15%) end fra modellen uden transformation. Standardfejlen på EC10-estimatet bliver en lille smule mindre med Box-Cox transformationen end for modellen uden transformation. For Herbicid 2 er billedet det samme, en forøgelse af standardfejl på EC50-estimatet og en reduktion af standardfejl på EC10-estimatet (reduktion på ca. 29%).
5.1.3 Sammenfattende bemærkninger
Justering for variansheterogenitet med en Box-Cox transformation kan resultere i ganske betydelige ændringer i præcisionen (mellem 15%-29%). Ikke nok med at man får en misvisende standardfejl på regressionsparametrene og dermed på EC-værdier, hvis der er variansheterogenitet, men de sædvanlige tests vil også give misvisende resultater.
5.2 Justering for variation fra kurve til kurve
5.2.1 Problemstilling
Vi betragter et dosis-responseksperiment, som blev udført for at undersøge, om der er hormonforstyrrende effekter af et stof. Nogle gange er man pga. praktiske begrænsninger nødt til at gentage det samme eksperiment flere gange over tid, og dermed melder spørgsmålet sig, om hvorledes man kan beskrive variationen indenfor og mellem forskellige uafhængige eksperimenter af samme stof i samme biologiske system.
5.2.2 Datakilde
Data er luminiscens-målinger på celler som funktion af vinclozolin (doseringsområde: 0,025-3,1 mM). Forsøget er gentaget 6 gange. Forskelle fra forsøg til forsøg kan forventes, idet der kan være forskel på dage, laboranter, temperatur og en række andre parametre som ændrer sig fra forsøg til forsøg. I Figur 5.3 kan man se data som er dosis-responskurver med et mere eller mindre forskelligt udseende, men dog især med forskellige øvre grænser.
Vi benytter en tre-parameter log-logistisk model og antager dermed a priori, at den nedre grænse er 0. Først analyseres datasættet, som om der var uafhængighed mellem målinger, både inden for en kurve og på tværs af kurverne (data slås sammen henover forsøgene og én dosis-respons-kurve bliver tilpasset). Det giver følgende estimater med standardfejl i parentes:
Hældning (b): 0,48 (0,11)
Øvre grænse (d): 1967 (161)
EC50: 0,08 (0,04)
med en estimeret residualstandardfejl på 396 (50 frihedsgrader). Bemærk at standardfejlen på EC50 er så stor at det er lige før EC50 ikke er forskellig fra 0.
En analyse, der reducerer effekten af forsøgsspecifikke forskelle, kan baseres på en ikke-lineær regressionsmodel med tilfældige virkninger (Pinheiro & Bates, 2000). Vi kan derfor bruge en ikke-lineær regressionsmodel med tilfældige forsøgsspecifikke effekter knyttet til den øvre grænse, ifølge Figur 5.3 er den parameter (d), der formentlig der har de største udsving fra et forsøg til et andet. Ved at benyttet denne udvidelse af ovenstående model, fås følgende resultater:
Hældning (b): 0,47 (0,04)
Øvre grænse (d): 1976 (299)
EC50: 0.08 (0,02)
med en estimeret standardfejl for de tilfældige effekter (forsøg-til-forsøg variationen) og residualleddet på henholdsvis 695 og 151. Sammenlignet med ovennævnte estimerede residualstandardfejl på 396 fra modellen uden tilfældige effekter kan man se, at modellen med tilfældige effekter har trukket mere variation ud, fordi det har været muligt at tage højde for den store variation fra forsøg til forsøg. Det er afspejlet i estimatet på 695, der er betydeligt større end residualstandardfejlen på 151. Og sidst men ikke mindst det afspejler sig i en halvering af standardfejlen for EC50.
Et statistisk likelihood ratio-test (Pinheiro & Bates, 2000, s. 83) viser, at modellen med tilfældige virkninger er signifikant bedre end modellen uden tilfældige effekter (p-værdi < 0,0001). Det ses ligeledes, at selve estimaterne næsten ikke ændrer sig, men derimod er der store forskelle på de estimerede standardfejl. F.eks. halveres usikkerheden på den estimerede EC50 ved at bruge modellen med tilfældige virkninger.
I Figur 5.3 ses den estimerede dosis-respons-kurve baseret på modellen med tilfældige virkninger samt individuelle (forsøgsspecifikke) estimerede kurver. Eksempelvis viser de 2 lodrette, røde pile forskydninger fra det gennemsnitlige overordnede responsniveau og til 2 af de individuelle forsøg; i det ene tilfælde er der tale om en forskydning opad svarende til et større responsniveau end det gennemsnitlige, mens det i det andet tilfælde er tale om en forskydning nedad. Disse 2 forskydninger samt de 4 øvrige forskydninger (som ikke er illustreret i Figur 5.3) forklarer modellen vha. de forsøgsspecifikke tilfældige effekter.
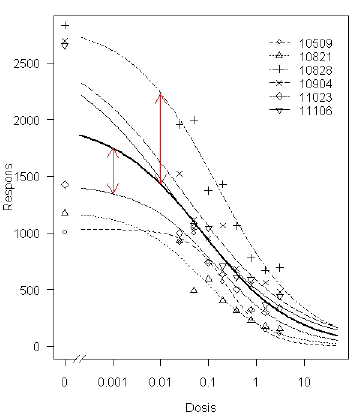
Figur 5.3. Estimeret dosis-responskurve baseret på modellen med tilfældige virkninger (den tykke sorte linje). De individuelle forsøgsspecifikke kurver er også indtegnet. For 2 af de individuelle kurver er forskydningerne fra det gennemsnitlige niveau vist med lodrette, røde pile.
5.2.3 Sammenfattende bemærkninger
Vi har analyseret ovennævnte datasæt vha. to forskellige statistiske modeller: En model hvor vi så bort fra at data kom fra seks forskellige forsøg, og en model hvor der også blev taget højde for variation fra forsøg til forsøg vha. tilfældige effekter. Modellen med tilfældige effekter gav et klart bedre resultat i form af en reduceret standardfejl på EC50.
Der er yderligere den fordel, at alle kurver bliver analyseret på en gang, og der er således ikke behov for at estimere individuelle kurver for hvert forsøg, hvorfra estimater så efterfølgende skal kombineres. Modeller med tilfældige effekter giver mulighed for at opsummere flere kurver, der svarer til samme behandling, men som varierer pga. eksperimentelle forskelle. En af ulemperne er, at sådanne ikke-lineære regressionsmodeller med tilfældige effekter kan være svære at få til at konvergere (at få estimationsproceduren til at virke). Hvis det ikke lykkedes at opnå konvergens for en model med tilfældige effekter, så tyder det ofte på, at der ikke er information nok i data til at kunne anvende en sådan model. I sådanne tilfælde må man gå tilbage til modellen uden tilfældige virkninger. Modeller med tilfældige virkninger kan også benyttes til at tage højde for gentagne målinger på samme organisme.
Version 1.0 Oktober 2008, © Miljøstyrelsen.