Statistisk analyse og biologisk tolkning af toksicitetsdata
4 Problemer, der er uafhængige af typen af respons
- 4.1 Sammenligning af ED/EC-værdier
- 4.2 Design af bioassays: Flere doseringer kontra flere replikater
- 4.3 Modelvalgets indflydelse på estimater for EC-værdier
I dette afsnit vil vi gennemgå de problemstillinger vi har identificeret ved at analysere en lang række datasæt fra projektdeltagerne. Ikke alle problemstillinger er lige godt belyst med data, men vi har bestræbt os på at vælge bioassay fra de forskellige discipliner projektgruppen repræsenterer. Generelt kan det anføres at problemstillingerne alle er så generelle, at de ikke er disciplinorienteret. De statistiske problemer som toksikologen tumler med er stort set de samme som økotoksikologens. Forsøgsorganismer kan være forskellige, men problemstillingerne er ofte de samme.
4.1 Sammenligning af ED/EC-værdier
4.1.1 Problemstilling
En af de oftest benyttede metoder til at vurdere pesticiders toksicitet og økotoksicitet er at sammenligne EC/ED-værdier fra forskellige, uafhængige bioassay/eksperimenter. Sådanne bioassay har ofte forskellige variansstrukturer, og så er spørgsmålet hvordan man bedst sammenligner?
4.1.2 Datakilde
Som eksempel benyttes et dosis-respons-forsøg, der belyser effekten af de to herbicider bentazon og glyfosat ved en række doseringer. Formålet med forsøget var at undersøge de to herbiciders virkning på hvid sennep (Sinapis alba). Responsen er tørvægt i g/potte (Christensen et al, 2003). Bioassays for de to herbicider blev udført uafhængigt af hinanden. Data består af målte responser ved forskellige doser af hvert herbicid svarende til to dosis-responskurver. En 4-parameter log-logistisk model (Ligning (2.1a)) blev tilpasset data. Estimater for EC20 på logaritmisk skala for bentazon og glyfosat var henholdsvis 3,11 (0,11) og 3,62 (0,15) med standardfejlen angivet i parentes. De tilbage-transformerede værdier er henholdsvis 22,3 med 95%-konfidensinterval (18,1 ; 27,6) og 37,3 med 95%-konfidensinterval (27,3 ; 50,8).
4.1.3 Analyse af data
På grundlag af regressionsanalysen vil vi undersøge om de to EC20 værdier er forskellige fra hinanden. Med andre ord, vi vil undersøge, om det kan antages, at differensen mellem estimaterne for log(EC20) for de to herbicider er signifikant forskellig fra nul.
Standardfejlen på forskellen på log(EC201)-log(EC202) kan beregnes ud fra standardfejlen på de to estimater (som vi nedenfor henholdsvis kalder se1 og se2 vha. følgende formel:
standardfejl på differensen = ![]()
Effekten af forskellige variansstrukturer i to uafhængige bioassay vil være inkluderet i de to standardfejl. Ud fra standardfejlen for differensen er vi i stand til at udregne et approksimativt 95%-konfidensinterval for differensen mellem de to log(EC20)-estimater:
differens på log(EC20)-estimater ± 1,96 ![]()
I ovenstående formel benyttes 1,96, dvs. 97,5%-fraktilen fra en standard normalfordeling. For kontinuerte data skulle man strengt taget i stedet for 1,96 bruge 97,5%-fraktilen fra en passende t-fordeling, men i langt de fleste tilfælde vil det ikke gøre nogen væsentlig forskel.
Baseret på 95%-konfidensintervallet kan man så teste (på signifikansniveau 5%), om der er forskel på de to EC-værdier ved at se, om 0 ikke er indeholdt eller er indeholdt i intervallet. Vi vil kalde denne test-procedure for differens-testet eller ratio-testet (Wheeler et al, 2006).
Regneeksempel: For ovenstående data fås følgende estimerede log(EC20)-værdier med standardfejl i parentes:
Bentazon: 3,11 (0,11)
Glyfosat: 3,62 (0,15)
Differensen på estimaterne er 3,11 – 3,62 = -0,51, og den tilhørende standardfejl vil være: ![]() = 0,19. Et approksimativt 95%-konfidensinterval for differensen bliver så:
= 0,19. Et approksimativt 95%-konfidensinterval for differensen bliver så:
-0,51 ± 1,96 · 0,19 = [-0,88 ; -0,14]
Konfidensintervallet indeholder ikke tallet 0, så vi kan konkludere, at der er forskel på EC20-værdierne for de to herbicider (på et 5%-signifikansniveau).
Hvis man sammen med de estimerede EC-værdier får oplyst de tilhørende 95%-konfidensintervaller i stedet for standardfejl, kunne man være fristet til at sammenligne konfidensintervallerne direkte og konkludere, at der ikke er forskel, såfremt de to intervaller overlapper. Wheeler et al (2006) fraråder denne metode, fordi den har betydelig mindre styrke mht. at finde forskelle end differens-testet, der direkte sammenligner de to estimerede EC-værdier: Overlap-proceduren kan godt vise, at de to EC-værdier er ens, hvor de i virkeligheden (vurderet ud fra differens-testet som er vist ovenfor) er forskellige. Omvendt vil det være sådan, at hvis man ud fra overlap-proceduren finder, at de to EC-værdier er forskellige, så vil differens-testet også vise, at der er forskel på de to EC-værdier. Opsummerende må det siges, at overlap-proceduren kan give misvisende resultater og derfor frarådes det at bruge den.
Regneeksempel fortsat: Ved at tilbagetransformere fra logaritmisk skala fås følgende EC20-estimater med tilhørende, individuelle konfidensintervaller:[1]
bentazon: 22,3 (18,1 ; 27,6)
glyfosat: 37,3 (27,3 ; 50,8)
De to intervaller overlapper hinanden, og baseret på overlap-proceduren ville vi konkludere, at de to EC20-værdier ikke er forskellige fra hinanden. Men det er i modstrid med resultatet fra differens-testet. Altså giver overlap-proceduren anledning til et misvisende resultat.
Man kan ofte ud fra konfidensintervallet regne tilbage til den benyttede standardfejl og på den måde få fat i standardfejlene for de 2 estimerede EC-værdier. Fremgangsmåden er som følger:
- Kontroller om intervallet er symmetrisk omkring den estimerede EC-værdi i lineær eller logaritmisk skala. Det kan nemlig kun lade sig gøre med symmetriske konfidensintervaller.
- Tag det venstre endepunkt i intervallet og fratræk den estimerede EC-værdi eller log(EC)-værdi og divider derefter med -1,96 for binomialfordelte data (eller eventuelt en passende 97,5%-fraktil fra en t-fordeling for kontinuerte data). Det fremkomne tal er standardfejlen på den estimerede EC-værdi eller log(EC)-værdi.
- Gentag det samme for det andet interval.
- Herefter kan ovenstående procedure benyttes til at sammenligne EC- eller log(EC)-værdierne.
Regneeksempel: Antag er EC50 i et givet dosisrespons assay er estimeret til 16,6 med et 95%-konfidensinterval på [15,2 ; 18,0]. Så giver følgende udregning den tilhørende standardfejl:
(15,2 – 16,6) / (-1,96) = 0,71
4.1.4 Sammenfattende bemærkninger
Såfremt både estimatet og den tilhørende standardfejl er angivet for dosis-responskurverne, så er det muligt at teste om de to EC-værdier kan være ens. Bemærk, at det er antaget, at de to forsøg, som skal sammenlignes, er uafhængige af hinanden. Så metoden kan ikke benyttes til at sammenligne forskellige endpoints fra samme test.
Anbefaling: Såfremt det er muligt at beregne et konfidensinterval for differensen mellem to logaritme-transformerede EC-værdier, så bør denne testprocedure benyttes. Kun i tilfælde hvor det ikke er muligt, bør overlap-proceduren benyttes.
4.2 Design af bioassays: Flere doseringer kontra flere replikater
4.2.1 Problemstilling
Et ofte diskuteret spørgsmål er, om det er bedre at have flere doseringer og færre replikater per dosis end omvendt? Vi betragter den situation, hvor der a priori er valgt et doseringsskema, hvorfra doseringer kan vælges. I praksis vil man ofte udføre et indledende studie med en koncentrationsrække, der spænder over flere dekader. Resultaterne herfra vil så blive brugt til at vælge doseringsrækken, som helst skal dække dosis der næsten ikke giver nogen virkning til doseringer der giver maksimal virkning. Hvis man overhovedet ikke har nogen idé om, hvilke doseringer der skal benyttes, så kan man f.eks. benytte metoden foreslået af Wright & Bailer (2007), som går ud på at man ud fra et valgt optimalitetskriterium bruger en computer-intensiv søge-algoritme til at finde de sæt af doseringer der bedst opfylder optimalitetskriteriet.
4.2.2 Datakilde
Vi vil benytte data fra et eksperiment, som undersøger virkningen af forskellige fenoler på rajgræs (Lolium perenne L). Respons er rodlængde for varierende koncentrationer af ferulsyre i mM, dvs. vi betragter et eksempel med kontinuert respons. Data bruges til at estimere de parameterværdier som alle datasæt (i scenario A nedenfor) simuleres ud fra.
4.2.3 Simulationsstudie
Med en fire parameter log-logistisk regression fik vi en EC50-værdi på 3,06 mM. Ved forsøget blev følgende doseringer anvendt:
0,23; 0,47; 0,94; 1,88; 3,75; 7,50; 15; 30; 60 mM
Data bruges til at generere de parameterværdier, der er nødvendige for at foretage de simuleringer der vises nedenfor. Der blev genereret 1000 datasæt baseret på en log-logistisk model for hvert af de to scenarier, A og B er vist i Tabel 4.1.
Tabel 4.1. EC-værdier anvendt til datagenerering i de to scenarier til illustration af betydning af replikater i dosis-responsforsøg.
| Scenarie | EC10 | EC50 | EC90 |
| A | 1,46 | 3,06 | 6,39 |
| B | 0,71 | 3,06 | 13,23 |
For såvel scenario A som scenario B var standardafvigelsen på målefejlen 0,52. Parametrene for scenario A er baseret på ovenstående datasæt, mens scenario B er fremkommet ved en modificering af parametrene, som spreder EC-værdierne mere ud på dosis-aksen (EC10 og EC90 ligger længere fra EC50 end i scenario A). De benyttede doseringer er som nævnt ovenfor.
Betydningen af gentagelser kontra dosering/koncentrationer med kun en gentagelse er undersøgt ved tilfældig udtrækning af doseringer i den ovennævnte doseringsrække. Hvis for eksempel fem doseringer blev simuleret, så blev de fem doseringer trukket tilfældigt (uden tilbagelægning) ud fra ovenstående doseringer. På tilsvarende vis blev de øvrige doseringer udtrukket (fra 6-9 doseringer). Der findes flere andre måder at udvælge doseringerne på, f.eks. kunne man starte med endepunkterne og så efterfølgende udvælge de resterende doseringer baseret på passende fraktiler. Hvis f.eks. 3 doseringer skal udvælges, så bliver den tredje valgt som medianen i fordelingen af doseringer.
For hvert datasæt er standardfejlen på EC10 og EC50 udregnet og efterfølgende blev den empiriske standardafvigelse over de 1000 datasæt fundet for hver af EC10 og EC50. I Figur 4.1 er parametrene for Scenario A benyttet og i Figur 4.2 er parametrene for Scenario B benyttet. Forskellen mellem scenario A og B er, at i B er der større afstand mellem EC10, EC50 og EC90 end i A.
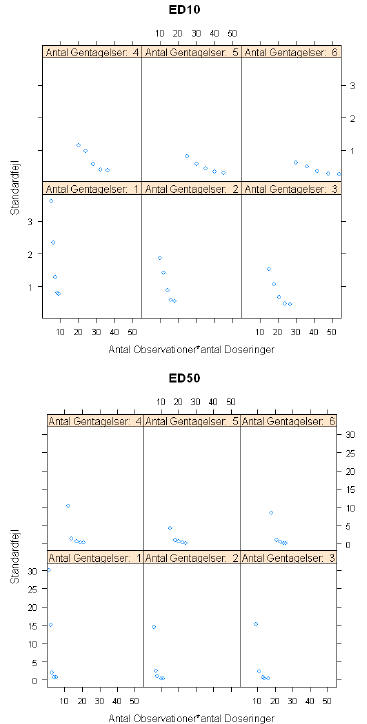
Figur 4.1. Simulerede standardfejl ved forskellige kombinationer af gentagelser og doseringer for Scenario A i Tabel 4.1.
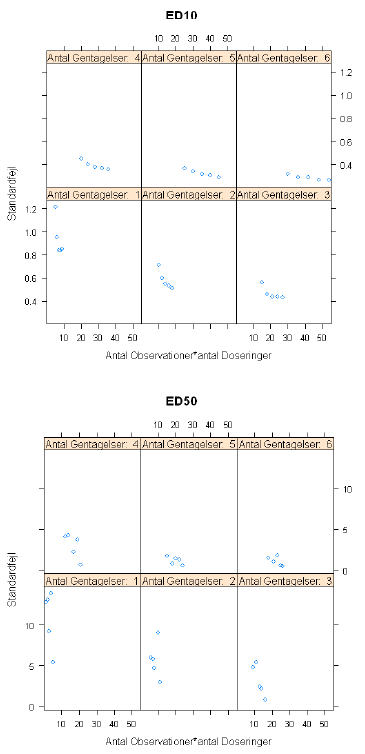
Figur 4.2. Simulerede standardfejl ved forskellige kombinationer af gentagelser og doseringer for Scenario B i Tabel 4.1.
4.2.4 Sammenfattende bemærkninger
For scenario A f inder vi for EC10, at 9 doseringer med 1, 2 og 3 replikater per dosering (9, 18, 27 observationer) giver betydelig mindre standardfejl (ned til en halvering) end 5 doseringer med henholdsvis 2, 4 og 6 replikater (10, 20, 30 observationer). Billedet er det samme for EC50, idet standardfejlen er betydeligt mindre for 9 doseringer med 1, 2 og 3 replikater per dosering (9, 18 og 27 observationer) end for 5 doseringer med henholdsvis 2, 4 og 6 replikater (10, 20 og 30 observationer). For scenario B er billedet det samme, om end forskellen mellem standardfejlen er knap så stor.
Sammenfattende kan det konkluderes, at den højeste præcision på EC10 og EC50, når der er restriktion på det samlede antal observationer, opnås ved at bruge flere doseringer frem for at bruge flere replikater (i nogle tilfælde opnås en ganske betydelig forbedring af præcisionen).
For at kunne belyse denne problemstilling er der blevet udviklet en funktion til udvidelsespakken drc til R, således at det er muligt ud fra et sæt af modelparametre (f.eks. fra et tidligere studie svarende til det nuværende eksperiment eller baseret på værdier fra litteraturen) samt et sæt af doseringer at få beregnet en tabel, hvor simulerede, gennemsnitlige standardfejl for valgte ED-værdier bliver angivet for forskellige antal replikater.
4.2.4.1 Eksempel med R
Vi ønsker at simulere en dosisresponskurve med en fire-parameter log-logistisk model (ligning 2.1.a)og vi antager (f.eks. ud fra tidligere forsøg) at modellen kan beskrives med parametrene: b=3, c=1, d=8, e=EC50=10. Desuden antages en residual standardfejl på 0,5.
Som udgangspunkt ønsker vi at bruge følgende doseringer mellem 0, 64, 2 og 32, men med mulighed for at tilføje doseringerne 4,16 og 8 (i den nævnte rækkefølge) en for en. Disse valg specificeres på følgende måde ved at angive en række argumenter i R-funktionen simDR:
simDR(c(3, 1, 8, 10), 0.5, LL.4(), c(0, 64, 2, 32, 4, 16, 8), noSim=1000, noRep=6)
Beregningerne er baseret på 1000 simulationer for ED10 og ED50, fra 1 og op til 6 replikater. Resultatet er nedenstående udskrift i R:
Average 'se' based on 1000 simulations
Concentrations used: 0 64 2 32 4 16 8
EC value considered 10 (TRUE: 4.81)
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 4 | 6.565232 | 6.182361 | 4.938106 | 3.7430477 | 2.3500168 | 2.5023711 |
| 16 | 4.503998 | 3.635206 | 2.341566 | 3.2517200 | 1.6776820 | 1.8352134 |
| 8 | 2.146454 | 2.161131 | 1.354035 | 0.8917755 | 0.7681428 | 0.6890755 |
EC value considered 50 (TRUE: 10)
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 4 | 8.349600 | 24.492790 | 6.126075 | 4.891222 | 3.9353017 | 4.3904793 |
| 16 | 2.575200 | 3.782776 | 2.525893 | 2.080585 | 1.4595111 | 1.3772345 |
| 8 | 1.602380 | 1.838767 | 1.244030 | 0.636938 | 0.6240596 | 0.8164947 |
Ovenstående udskrift viser de gennemsnitlige standardfejl på EC10 og EC50 baseret på 1000 simulationer fra en log-logistisk model med parametre b=3, c=1 (nedre grænse), d=8 (øvre grænse) og e=EC50=10. I hvert simulationstrin estimeres 3·6=18 modeller: 6 modeller med 5 doseringer (0, 2, 4, 32 og 64) med antal replikater fra 1 til 6, 6 modeller med doseringer (0, 2, 4, 16, 32 og 64) med antal replikater fra 1 til 6 og endelig 6 modeller med 7 doseringer (0, 2, 4, 8, 16, 32, 64) med antal replikater fra 1 til 6. For hver estimeret model i hvert simulationstrin udregnes standardfejlen for EC10 og EC50. Gennemsnit over de 1000 simulations for EC10 og EC50 for hver kombination af antal doseringer (fra 5 til 7) og antal replikater (fra 1 til 6) er vist i udskriftet.
Igen ses det, at for det valgte scenario opnås en betydelig bedre præcision ved at tilføje flere doseringer i forhold til at bruge flere replikater. F.eks. er der for EC50 mere end en faktor 10 til forskel på at bruge alle 7 doseringer en gang i forhold til blot at bruge de 5 doseringer: 0, 2, 4, 32, 64 to gange hver.
4.3 Modelvalgets indflydelse på estimater for EC-værdier
4.3.1 Problemstilling
I det følgende undersøges om valget af dosis-respons model har afgørende indflydelse på estimerede EC-værdier.
4.3.2 datakilde
Data stammer fra det samme eksperiment hvor den kombinerede effekt af forskellige fenoler på rajgræs (Lolium perenne L) blev undersøgt. Data bruges til at estimere de parameterværdier som alle øvrige datasæt simuleres ud fra. Igen betragtes et eksempel med kontinuert respons.
4.3.3 Simulationsstudie
Der blev genereret 1000 datasæt baseret på hver af følgende modeller: log-logistisk, Weibull-1 og Weibull-2 (Seber & Wild, 1989, pp. 338–339). For alle 3 modeller blev følgende doseringer benyttet:
0,00; 0,94; 1,88; 3,75; 7,50; 15,00; 30,00
med 6 replikater for dosering 0 og 3 replikater for de øvrige doseringer.
For den symmetriske log-logistiske model blev følgende parameterværdier benyttet til at generere datasættene:
b = 2,98 c = 0,48 d = 7,79 EC50 = 3,06
med standardafvigelse på målefejlen på 0,52.
For den asymmetriske Weibull-1 model (langsomt aftagende fra den øvre grænse) blev følgende parameterværdier benyttet:
b = 2,39 c = 0,66 d = 7,81 e = 3,60
med standardafvigelse på målefejlen på 0,55. Bemærk at parameteren e i Weibull-1 ovenfor og Weibull-2 nedenfor er vendetangenten, som netop i de to tilfælde ikke er midt på kurven
Endelig blev der for den asymmetriske Weibull-2 model (hurtigt aftagende fra den øvre grænse) benyttet parameterværdierne:
b = -1,97 c = 0,32 d = 7,73 e = 2,49
standardafvigelse på målefejlen var på 0,51. Parametrene c og d svarer i alle tre modeller til henholdsvis den nedre og øvre grænse. Figur 4.3 illustrerer forskellene mellem modellerne (kurverne er tegnet ud fra de ovenfor angivne parametre).
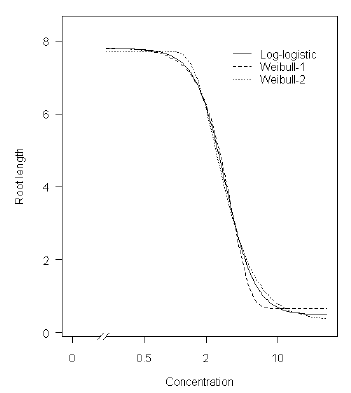
Figur 4. 3. Illustration af de tre 4-parameter-dosis-responsmodeller: den log-logistiske model (fuldt optrukne kurve), Weibull-1-modellen (lange stiplede kurve) og Weibull-2-modellen (korte stiplede kurve).
Tabel 4.1 viser absolut og relativ bias, som er den gennemsnitlige differens mellem den estimerede EC-værdi og den rigtige EC-værdi (for det relative bias er differensen endvidere blevet divideret med den rigtige EC-værdi), og mean square error (MSE), dvs. den gennemsnitlige (kvadratiske) afstand fra den estimerede EC-værdi og til den rigtige EC-værdi for de tre modeller.
Tabel 4.1. Absolut og relativ bias samt ”Mean Square Error” MSE (i parentes) er angivet under hinanden i hver celle for de tre modeller: Først vises resultater, hvor der er simuleret fra den log-logistiske model, dernæst vises resultater baseret på Weibull-1-modellen og til sidst resultater fra Weibull-2-modellen.
| Estimeret model | ||||||
| Log-logistisk | Weibull 1 | Weibull 2 | ||||
| Simuleret model | Log-logistisk | EC10 1,46 |
Absolut bias Relativ bias MSE |
0,088 0,060 0,21 |
-0,033 -0,023 0,26 |
0,26 0,18 0,30 |
| EC50 3,06 |
Absolut bias Relativ bias MSE |
0,064 0,021 0,16 |
0,12 0,04 0,16 |
0,022 0,0071 0,23 |
||
| Weibull 1 | EC10 1,41 |
Absolut bias Relativ bias MSE |
0,24 0,17 0,30 |
0,09 0,064 0,27 |
0,43 0,30 0,50 |
|
| EC50 3,09 |
Absolut bias Relativ bias MSE |
-0,0089 -0,0029 0,14 |
0,053 0,017 0,12 |
-0,079 -0,025 0,19 |
||
| Weibull 2 | EC10 1,63 |
Absolut bias Relativt bias MSE |
-0,084 -0,052 0,18 |
-0,17 -0,10 0,29 |
0,066 0,041 0,18 |
|
| EC50 3,00 |
Absolut bias Relativ bias MSE |
0,13 0,045 0,19 |
0,29 0,067 0,20 |
0,10 0,033 0,27 |
||
4.3.4 Sammenfattende bemærkninger
Ud fra Tabel 4.1 kan vi konstatere, at der ikke ser ud til at være store forskelle på de estimere EC50-værdier, uanset hvilken model der blev brugt til at generere simulerede data. Bias i estimater bliver lidt større for EC10, hvis den forkerte model bruges og det samme vil gøre sig gældende for EC90 (data ikke vist).
Fodnoter
[1] ( exp(3,11 - 1,96 * 0,11) , exp(3,11 + 1,96 * 0,11) ) for konfidnesintervallerne og exp(3,1) for parameterestimetet
Version 1.0 Oktober 2008, © Miljøstyrelsen.