Guidelines on remediation of contaminated sites
Appendix 5.3
Evaporation of volatile substances from soil
1. Background
For soil or groundwater contamination by volatile substances, these substances might evaporate, causing danger of inhalation of harmful fumes both in open areas and indoors.
Evaporation from soil will often be one out of several contributors outside as well as indoors. Other contributions to air contamination will come from traffic, neighbouring enterprises, gas emission from construction materials etc. as well as from smoking, leisure activities/hobbies and so forth.
This Appendix provides a description of the principles of calculating the resultant contribution to indoor and outdoor air concentrations from volatile organic contaminants in soil.
Data regarding the following issues are used as the basis for calculations:
| contamination type and concentration, including physico-chemical data for the specific contamination components | |
| depth of contamination and its relative position to the groundwater table | |
| soil strata condition | |
| building parameters | |
| temperature and pressure conditions | |
| wind velocities etc. |
Building parameters include the following data:
| constructions on soil. Wooden floors or concrete floors. If floors are concrete, environmental classification, reinforcements conditions, the age of the floor etc. must be determined. | |
| ventilation conditions of the building. | |
| ceiling heights of rooms. |
Models for calculation of release and transport of vaporous components in soil are a relatively new occurrence, and not all formulae are equally well supported by experiments. In Denmark as well as elsewhere, work is continuously being done to acquire better knowledge of the mechanisms governing evaporation of volatile substances from soil, but as yet, models for calculating contributions from contaminated soil to indoor air and outdoor air are subject to a relatively high degree of uncertainty.
The fundamental model of calculation described here comprises three parts:
| Phase distribution in soil, i.e. the distribution of individual contamination components between soil gas, soil water, a phase adsorbed to the soil matrix and possibly NAPL contamination. Using this data, soil gas concentrations of contaminants can be calculated on the basis of total soil contaminant concentrations. | |
| Diffusion up through the soil and floor constructions: Here, evaporation through the soil is calculated on the basis of contaminant concentrations in the soil gas of the contaminated zone and the relative depth to this zone. Diffusion contributions to indoor air and outdoor air are subsequently calculated on the basis of this evaporation. | |
| Convection through floor constructions: Convection contribution to indoor air is calculated on the basis on the previously calculated diffusive transport to the undersurface of the building. |
2. Calculation principles and assumptions
2.1 Phase distribution
In cases where contamination is situated in the unsaturated zone, where consequently the soil contains soil particles, soil water and soil gas, soil gas concentrations can be calculated when the phase distribution of the substance between these three phases – and any contamination with a NAPL - is known.
This calculation could be carried out using a model which among other places is described in Mackay & Paterson, 1981 /5/.
In its simplest form, the model assumes equilibrium of contamination-component content in the different phases and constant conditions. In addition to this, the model assumes that contamination components in their vaporous phases behave as ideal gases, and that components in their aqueous phases behave as ideal diluted solutions. Other versions of the model exist capable of taking into account that equilibrium has not occurred, and that decomposition and/or transport of substances is occurring. In the following, the simplest version of the model is the basis of the description.
The principle of the calculation is that the soil’s maximum capacity for contamination components is calculated on the basis of saturation concentrations in air and water and the distribution ratio between water and soil particles. It is then assumed that the distribution ratio between the three phases will be the same as they would be in case of saturation, even given other concentrations, and that equilibrium has been established. Soil gas concentration at a given total concentration can be calculated on this basis.
If contamination occurs in the groundwater, soil gas concentrations just above the groundwater table can be determined – again, assuming equilibrium between the two phases – on the basis of the relationship between the contamination component’s partial pressure in air and solubility in water (Henry's law). It must be noted that diffusion in the aqueous phase is several orders less than diffusion in the vaporous phase, and that for this reason, aqueous-phase diffusion could limit evaporation from the groundwater to soil gas in the unsaturated zone. No account is taken of this in the calculations.
For contamination caused by products consisting of several components (such as oil and tar), individual components may interact, for instance by dissolving in each other or possibly by reacting chemically with each other. This influences vapour pressure as well as solubility and adsorption of individual components. However, for mixtures made up of neutral components (for instance oil) this deviation will be minor in relation to the other uncertainties in the calculations.
If organic acids are part of the mixture (such as for instance phenol in tar), the deviation will be significant, especially as regards the organic acid (for phenol in tar the resultant vapour concentration will typically be smaller by a factor of 10 due to the mixture). In principle, account can be taken of this by including activity coefficients in the equilibrium expression for individual components in the relevant mixture.
In connection with calculations for mixtures, account must always be taken of the ratio of mixture by involving the molar fraction for each individual component and during each separate stage of calculation.
2.2 Gaseous transport through soil
The model for evaporation described here is solely concerned with diffusive transport in the soil gas in soil. In connection with soil contamination, gas generation resulting in positive pressure is rare except, for example, in cases involving contamination components placed at an actual landfill. For this reason, convective transport through soil strata can be discounted in such cases.
Substance-specific parameters aside, the diffusion of a contamination component will depend on soil type and soil porosity and water content. In addition to this, the soil may comprise several strata with different properties.
Variations in barometric pressure may cause a certain pumping effect, consequently causing a flow of air in the topmost soil strata. Similarly, ventilation in buildings situated near the contaminated soil can also cause convective air flow in the soil, air flow which influences vapour transport; as will significant differences in temperature.
In connection with a contamination component’s diffusion through soil strata, double solution in seeping rainwater and sorption onto soil particles could occur. In constant conditions and on average, double solution in rainwater for soil strata up to a thickness of a couple of metres will be 1-2 orders less than the diffusive rising flux, and consequently will be of no significance. With larger amounts of water seeping over a shorter period of time, double solution may be significant.
Among other things, sorption on soil particles will depend on the water content of the soil, since sorption in damp soil will be up to two orders less than in dry soil.
Biological degradation, especially during summer, can probably cause a reduction of vapour concentration in certain contamination components in the uppermost soil strata, and hence a reduction of evaporation.
Conversely, the partial pressure of most contamination components will display considerable temperature dependence, causing an increase of evaporation during period of summer.
Finally, during hot summers and in green and cultivated areas, upward water transport in the soil due to evapotranspiration may occur. In principle, this can promote substance transport to the surface.
The simple model described here does not include convective transport through soil strata caused by any differences in pressure, nor does it address diffusion in soil water, double solution/sorption of vapours, degradation, temperature dependence, or evapotranspiration.
2.3 Diffusive contribution to outdoor air concentration
The diffusive contribution to concentration in outdoor air can be calculated based on the flux to the ground surface on the basis of e.g. the following assumption:
| Mixing of the evaporated contamination component occurs in the air within a certain height above ground level. This height depends on wind velocity and on the location of the desired point of concentration calculations. It is assumed here that the greatest concentrations are found downwind at the end of the contaminated site. |
2.4 Diffusive contributions to indoor air concentrations
The diffusive contribution to indoor air concentrations can be calculated on the basis of the flux to the undersurface of buildings based on the following assumption:
| diffusion of contamination components occurs to the undersurface of buildings and further upwards through floor constructions, | |
| the diffusive flux of contamination components are mixed with the indoor atmospheric environment in the room closest to the ground. |
2.5 Convective contributions to indoor air concentrations
The convective contribution to indoor air concentrations can be calculated on the basis of calculated diffusive to the undersurface of buildings under the following assumptions:
| calculations are made for only one type of floor, concrete deck, | |
| crack spacing and crack width can be estimated on the basis of the reinforcement conditions, thickness, and environmental classification of the concrete, | |
| the convective contribution to indoor air can be calculated on the basis of the estimated crack spacing and crack width in conjunction with building vacuum, | |
| the convective flux of contamination components through the concrete deck is mixed with the indoor atmospheric environment in the room closest to the ground. |
3. Calculation formulae
In the following, the formulae used in the calculation model are described in their simplest form, i.e. given all the simplifying assumptions that have been mentioned earlier. The objective is to provide a description of the order and principles of the calculations. In specific cases, careful consideration should be given to which simplifying assumptions can be made.
3.1 Phase distribution in soil
The total volume of soil can be seen as the sum of the soil phases, see equation 1.
Equation 1
VL + VV + VJ = 1
where:
VL = relative volumetric proportion of air in soil
VV = relative volumetric proportion of water in soil
VJ = relative volumetric proportion of soil particles in soil.
Here, VL + VV equals total porosity.
Maximum contaminant content of one cubic metre (1 m3)of soil distributed across the three phases can be calculated as follows, see Equations 2-10:
Equation 2
In the air phase of soil (soil gas):
ML, max = VL · CL, max (mg/m3)
where:
ML,max= maximum contaminant amount in soil gas (mg/m3 soil volume)
CL,max = saturated vapour concentration of contaminant (mg/m3 soil gas).
CL,max can be calculated on the basis of the contaminant’s partial pressure by means of the law of ideal gases:
Equation 3
![]()
where:
p =contaminant partial pressure (N/m2)
m =contaminant molecular weight (g/mol)
R =the gas constant (J/mol · K)
T = temperature in K.
T = 298 K (25oC) is used as standard.
In the water phase of soil (soil water):
Equation 4
MV,max = VV · S (mg/m3)
where:
MV,max = maximum contaminant amount in soil water (mg/m3 soil volume)
S = water solubility of contaminant (mg/m3 soil water).
At equilibrium, the relation between contaminant partial pressure and water-phase concentration equals constant of Henry’s law, H:
Equation 5
![]()
The use of Henry’s law assumes that in vapour form, the contaminant behaves like an ideal gas, and that in solution form, it behaves like an ideal diluted solution. Partial pressure and solubility must be registered at the same temperatures.
Equation 6
In the particle phase of soil:
MJ,max = VJ · d · Jmax · 103 (mg/m3)
Where:
MJ,max = maximum contaminant amount which has adsorbed to the organic fraction of soil particles (mg/m3 soil volume)
d = soil particle density (kg/l)
Jmax = amount of contaminant which adsorbs to the organic fraction of soil particles at equilibrium with saturated solution in water (mg/kg)
Jmax can be represented by S as follows:
Equation 7
Jmax = KD · S · 10-3 (mg/kg)
Where:
KD = contaminant ratio soil/water (l/kg).
Given the assumption that adsorption occurs only onto the soil’s organic-substance content, which can be a reasonable approximation as regards organic contaminants, KD can be calculated based on the contaminant’s ratio between organic carbon and water, and the soil’s organic carbon content.
Equation 8
KD = Koc · foc (l/kg)
Where:
Koc= contaminant ratio between organic carbon and water (1/kg)
foc =soil content of organic carbon (relative weight proportion).
Consequently, MJ,max can be written:
Equation 9
MJ,max = VJ · d · Koc · foc · S (mg/m3)
For most types of contaminants, the contaminant’s ratio between organic carbon and water can be estimated based on the octanol/water ratio Kow., "most types" indicating aromatics, PAHs, aliphatic hydrocarbons and chlorinated solvents, cf. Equation 10a. In connection with phenols, which are weak organic acids, pH is also included in the estimate, Equation 10b /6/.
Equation 10a
The following formula is used for contaminants with log Kow less than 5 and soil with foc greater than 0.1 %:
log Koc = 1.04 · log Kow – 0.84
In connection with organic acids (for example chlorophenols), KD can be calculated on the basis of:
Equation 10b
KD = foc · kow0,82 · (l.05 · Fn + 0.026 · (1-Fn))
Where: Fn = neutral acid fraction (unitless).
The neutral acid fraction can be calculated on the basis of:
![]()
where pKa = contaminant acid dissociation constant.
The formula applies if:
pH - pKa < 1.5 and foc > 0.001
It follows that the maximum soil capacity for contaminants (immediately preceding the occurrence of NAPL) will be:
ML,max + MV,max + MJ,max
The distribution of the contaminant onto the three soil phases can be calculated on the basis of the above-mentioned assumption that the relative proportion of the three phases in soil is independent of total soil concentration.
The following applies to the air phase of soil:
Equation 11
![]()
where:
fL =relative contaminant ratio in soil gas in proportion to total content (unitless).
ML,MV,M= actual/relevant contaminant amount in each of the three phases (mg/m3 soil).
On the basis of Equations 2, 4 and 9 and Equation 3 and 5, fL can be rewritten as follows:
Equation 12
![]()
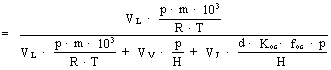

On the basis of a given total concentration in soil CT (mg/kg soil volume) the contaminant volume in the ML can then be established:
Equation 13
ML = fL · CT · r · 103 (mg/m3 soil volume)
where: r = soil density (kg/l)
Contaminant concentration in soil gas, CL, is then calculated on the basis of contaminant concentration in soil, CT, see Equation 14.
Equation 14
![]()
Remember that CL cannot exceed CL,max.
If the soil has a NAPL, i.e. saturated conditions, it is easiest to calculate CL = CL,max directly on the basis of the partial pressure, see Equation 3.
3.2 Diffusion up through soil
Given a state of equilibrium, gas transport from contaminated soil to the ground surface by means of diffusion in soil gas can be described by means of Fick’s law of diffusion:
Equation 15
![]()
where:
| J | = | flux (evaporation) (mg/(m2 · s)) | |
| N | = | material constant (unitless) | |
| DL | = | contaminant diffusion coefficient in air (m2/s) | |
| X | = | depth corresponding to concentration CL (m) | |
| Co | = | background concentration at the site (mg/m3), can be set at 0, if it is significantly less than CL. |
Equation 16
In connection with a number of substances, the diffusion coefficient in air can be found in Lugg /9/ or be estimated on the basis of the following formula /6/:
![]()
where:
D1 and D2 = diffusion coefficients in air of contaminants (m2/s)
m1 and m2 = contaminant molecular weights (g/mol)
If gas-phase transport occurs through various different soil strata the flux will be:
Equation 17
![]()
where: N1 to Nn are the material constants for the various strata and X1 to Xn each represent the thickness of each individual soil-strata.
One possible expression for N for soil would be, for example, Millington /8/.
Equation 18
N = (VL3,33 / (VL + Vv,)2)
where VL + VV is total porosity.
By substituting Equations 14 and 17 into Equation 15 and by assuming that Co can be set at 0, an expression for the flux up through the soil as a function of soil concentration is obtained:
Equation 19
![]()
![]()
3.3 Diffusive contribution to concentrations in outdoor air
The mixing of the flux J in outdoor air will result in a contribution to outdoor air concentration, Cu (mg/m3).
Given the assumption that the highest value for Cu is found downwind, at the end of the contaminated area, Cu can be calculated on the basis of the following assumption:
The mass-flow velocity, Q1, perpendicular up through the contaminated area equals the mass-flow velocity, Q2, through a vertical section perpendicular to the wind direction at the end of the contaminated area, given that diffusion in the air over the contaminated area is disregarded. This assumption is not unreasonable in connection with the relatively short distances involved here.
This gives the following:
Equation 20
Q1 = Q2 (mg/s) þ
A1 · J = A2 · v · Cu þ
l · b · J = b · h · v · Cu
or
![]()
where:
| Cu | = | diffusive contamination contributions to outdoor air (mg/m3) | |
| Q1 | = | mass-flow velocity up through the contaminated area (mg/s) | |
| Q2 | = | mass-flow velocity through a vertical section perpendicular to the wind direction (mg/s) | |
| v | = | wind velocity (m/s) | |
| A1 | = | area of contaminated area (m2) | |
| A2 | = | area of vertical section perpendicular to the wind direction (m2) | |
| l | = | length of the contaminated area in the wind direction (m) | |
| b | = | width of the contaminated area perpendicular to wind direction (m) | |
| h | = | mixing height in outdoor air at the downwind end of the contaminated area (m). |
In order for Cu to be comparable to the evaporation criteria for a substance, wind velocity, v, must in principle equal the velocity which can be measured at the point in question indicated as the 1% fractile.
Based on experience, at such low wind velocities v (£ 2 m/s) the mixing height, h, can be set at 0.08 times the length of the contaminated area, 1. If this is substituted into the Equation 20 the result is:
Equation 21
![]()
(J is determined by means of Equation 19).
or
Equation 22
J = Cu · v · 0,08 (mg/m2 · s)
A wind velocity of 0.1 m/s is used, which corresponds to calm conditions. However, a wind velocity of 1 m/s is used for substances where the criteria for acceptance are determined on the basis of long-term effects; this includes carcinogens.
3.4 Diffusive contribution to indoor air contamination concentration
The mixing of the flux J in the indoor air will result in an indoor air contribution, Ci (mg/m3).
The mass-flow velocity, Q1, perpendicular up through the contaminated area into the building equals the mass-flow velocity, , Q2, generated through air renewal in the building. This gives the following:
Equation 23
Q1 = Q2 (mg/s) þ
A1 · J = A2 · Lh · Ls · Ci
Given the conservative assumption that A1 = A2 (contamination occurs under the entire room), the following is arrived at:
Equation 24
![]()
where:
| Ci | = | diffusive contamination contribution to indoor air (mg/m3) | |
| Q1 | = | mass-flow velocity up through the contaminated area (mg/s) | |
| Q2 | = | mass-flow velocity generated through air renewal (mg/s) | |
| A1 | = | contaminated area (m2) | |
| A2 | = | building area (m2) | |
| Lh | = | ceiling height in building (m) | |
| Ls | = | air renewal in building (s-1) |
3.5 Convective and diffusive contribution through reinforced concrete deck to indoor air contamination concentration
The convection of contaminants can occur through cracks in concrete deck and through leaking joints and leaks in pipe lead-ins etc. Calculations regarding shrinkage cracks due to drying shrinkage can be carried out by means of formulae and directions which can be found in the Danish standard specifications for concrete constructions DS411 /3/ and in Beton-Bogen (‘The Concrete Book’) /4/.
The calculation of air transport through cracks have been carried out according to Baker, Sharples & Ward /7/.
3.5.1 Calculating crack length and width
The crack parameter aw can be calculated based on the following:
Equation 25
![]()
where
aw = crack parameter (mm)
Acef = active concrete area subject to tensile force (mm2)
dw = crack-determining diameters of reinforcement bars (mm)
The active concrete area subject to tensile force Acef can be calculated as:
Equation 26
Acef = hb × bb
where hb = thickness of concrete deck (mm)
bb = observed
concrete-deck width (mm)
Equation 27
dw = k · da
where da = nominal diameter of reinforcement (mm)
k = constant which depends on
the type of reinforcement, cf. the table below
Reinforcement |
k |
Ribbed bars & tentor steel |
1.0 |
Plain reinforcement |
0.5 |
Consequently the crack parameter will be
Equation 28
![]()
where Db = the distance between reinforcement bars (mm).
For b >> Db we have
Equation 29
![]()
The free shrinkage strain es can be estimated on the basis of the following empirical formula for the mean value
Equation 30
es = ec · kb · kd · kt
where
| es | = | shrinkage strain (%) |
| ec | = | base shrinkage (%) |
| kb | = | coefficient taking into account influences from the composition of concrete (unitless) |
| kd | = | coefficient taking into account dimension (unitless) |
| kt | = | coefficient taking into account shrinkage time (unitless) |
Base shrinkage can be calculated as
Equation 31
Base shrinkage can be calculated as
![]()
![]()
where RF = relative air humidity (%)
kb is calculated based on the composition of concrete
Equation 32
kb = 0.007 · CM · (v/c + 0.333) · v/c
where CM = cement content (kg/m3)
v/c = water/cement ratio (unitless)
The equivalent radius r and kd are calculated by means of the following formulae:
Equation 33
![]()
where r = equivalent radius of construction (mm)
Equation 34
![]()
The influence of time:
Equation 35
![]()
where ts = shrinkage time (days)
to, a and b are auxiliary parameters (unitless)
Equation 36
![]()
![]()
![]()
3.5.2 Calculating reinforcement tension
The calculation is carried out according to Beton-Bogen (‘The Concrete Book’) /4/.
The reinforcement ratio j is
Equation 37
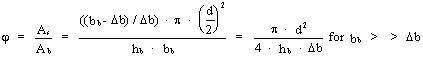
where
j = reinforcement ratio (unitless)
As = cross-sectional area of reinforcement (mm2)
Ab = cross-sectional area of concrete (mm2).
The modulus of elasticity n is
Equation 38
![]()
where
n = modulus of elasticity (unitless)
Es = coefficients of elasticity for steel (MPa)
Eb = coefficients of elasticity for concrete (MPa).
Compression stress of reinforcement
Equation 39
![]()
According to the Danish standard specification for concrete DS 411 /3/, crack width can be calculated by means of the formula:
Equation 40
![]()
where
w = crack width (mm)
s
s = reinforcement stress (MPa)aw = crack parameter (mm)
3.5.3 Calculating crack spacing
According to Beton-Bogen (‘The Concrete Book’) /4/, the smallest crack spacing can be calculated as:
Equation 41
![]()
where lm = smallest crack spacing (mm).
Average crack spacing is calculated as
Equation 42
lw = 1,5 × lm
where lw = average crack spacing (mm).
This formula applies to aw < 2000.
Equation 43
Total crack length is calculated as:
![]()
where
ltot = total crack length (m)
ll = floor length (m)
lb = floor width (m)
3.5.4 Calculating air transport through cracks
The following calculation of air transport through cracks is carried out according to Baker, Sharples & Ward /7/.
Volume flow through concrete deck is calculated by means of ‘Cubic Law’
Equation 44
![]()
where
Qb = volume flow through concrete deck (m3/s)
ltot = total crack length (m)
w = crack width (mm)
D P = pressure differential above concrete deck (Pa)
hb = concrete deck thickness (mm)
m = dynamic viscosity of air in the soil system (kg/m · s)
Volume flow q pr. m2 floor area will be
Equation 45
![]()
where Ag = floor area (m2) = ll · lb
Mass balance around floor:
Diffusion through soil equals the sum of diffusion and convection through concrete:
Equation 46
![]()
where
N1 = material constant for the soil stratum under the concrete deck, and x1 is its thickness.
Nb = material constant of concrete deck and xb is its thickness.
CL = contaminant concentration in soil gas at the contamination mg/m3).
CP = soil gas concentration under concrete deck (mg/m3).
CK = the sum of convective and diffusive contributions to indoor air concentration (mg/m3).
Q = volume flow (convection through floor cracks) pr. m2 of floor area.
DL = contaminant diffusion constant in air (m2/s).
Mass balance of building:
The flux out of the buildings equals the sum of convection and diffusion through the concrete floor.
Equation 47
![]()
where
Lh = ceiling height in building (m)
Ls = air renewal in building (pr. time)
Equations 46 and 47 give (two simultaneous equations):
Equation 48
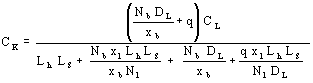
If the soil gas concentration CP is measured under floor, the contamination
contribution ![]() to indoor air can be
calculated using the following formula:
to indoor air can be
calculated using the following formula:
Equation 49
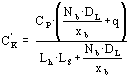
where ![]() = contamination
contribution calculated on the basis of the soil gas concentration measured (mg/m3).
= contamination
contribution calculated on the basis of the soil gas concentration measured (mg/m3).
If there are several different soil strata under the concrete deck, a total material constant and equivalent thickness can be calculated for all strata:
Equation 50
NJ = N1
Equation 51
![]()
where
NJ = the equivalent material constant of all soil strata
xJ = the equivalent thickness of all soil strata
4 Data regarding types of soil, concrete parameters and building parameters
Tables 1 to 3 provide values for relevant parameters for various types of soil, concrete parameters and building parameters.
For soil parameters, four different types of soil are indicated: two types of mould representing the plough layer in fields (sandy loam and loam), and two types of soil representing soil below the plough layer/root zone. The water content provided corresponds to dry soil, defined as soil with natural drainage.
However, if the upper soil strata have growth (e.g. in connection with the two types of mould), water content might drop to a level corresponding to a water content which is inaccessible to plants.
For each parameter, Table 1 provides an interval in the top line and a typical value in the bottom line.
Table 1
Data regarding types of soil.
|
Loam |
Sandy loam |
Clay |
Sand |
Porosity Vl + Vv, % (volume basis) |
35-45 40 |
40-45 45 |
35-45 40 |
35-50 45 |
Water content Vv, % (volume basis) |
25-35 30 |
15-35 35 |
20-40 30 |
5-35 15 |
Particle density, d, kg/l |
2.6-2.7 2.65 |
2.5-2.6 2.6 |
2.7-2.8 2.7 |
2.6-2.7 2.65 |
Volumetric density, r, kg/l |
1.4-1.8 1.7 |
1.4-1.7 1.6 |
1.5-1.8 1.8 |
1.4-1.7 1.7 |
Organic carbon content, foc, %, (weight basis) |
1 |
2 |
0.1 |
0.1 |
In fissured clayey till there is a secondary porosity from the fissures, which gives a
greater material constant depending on the water content of the matrix and fissures.
As regards concrete parameters for calculating the diffusive and convective contributions to indoor air, standard values are provided for a reinforced concrete deck as described in Diffusionsforsøg, betongulve (‘Diffusion tests, concrete floors’), issued by the National Housing and Building Agency /1/ and Radonvejledningen (‘The Radon Guidelines’) /2/.
Table 2
Data regarding concrete deck.
Material constant, N, unitless |
0.002 |
Reinforcement bar spacing, Db, mm |
50 |
Reinforcement diameter, da, mm |
3 |
Relative humidity, RF, % |
60 |
Cement content, CM, kg/m3 |
220 |
Water/cement ratio, V/C, unitless |
0.67 |
Shrinkage time, ts, days |
7300 |
Coefficient of elasticity for steel, Es, MPa |
210,000 |
Coefficient of elasticity for concrete, Eb, MPa |
20,000 |
As regards other building parameters, the following standard values may be used.
Table 3
Data regarding the building.
Pressure differential over concrete deck, D P, Pa |
5 |
Air renewal, Ls, s-1 |
8.3 · 10-5 |
Air renewal of 8.3 · 10-5 s-1 corresponds to 0.3 time-1.
S. 5.3.2 of the risk assessment for indoor airs mentions a dilution factor of 100. Using the following standard values:
Air renewal, LS = 8.3 · 10-5 s-1
Air height, Lh = 2.3 m
Concrete thickness, hb = 0.08 m
Pressure differential over concrete deck, D P = 5 Pa
a set of crack widths and lengths can be calculated for a floor of 100 m2, ensuring a dilution factor of 100, cf. Equations 45 and 49.
Table 4
Crack width and crack length
Crack width (mm) |
Crack length (m) |
0.1 |
640 |
0.2 |
70 |
0.5 |
4.7 |
1.0 |
0.6 |
Table 5
List of symbols.
Symbol |
Explanation |
Unit |
a |
Auxiliary parameter |
unitless |
aw |
Crack parameter |
mm |
b |
Auxiliary parameter |
unitless |
ec |
Base shrinkage |
% |
es |
Shrinkage strain |
% |
m |
Dynamic viscosity of air |
kg/m/s |
r |
Soil density |
kg/l |
ss |
Reinforcement tension |
MPa |
Fn |
Neutral acid fraction |
unitless |
j |
Reinforcement ratio |
unitless |
A |
Area |
m2 |
Acef |
Active concrete area subject to tensile force |
mm2 |
aw |
Crack parameter |
mm |
b |
Contaminated area width |
m |
bb |
Considered width of concrete deck |
mm |
Db |
Reinforcement-bar spacing |
mm |
Ci |
Diffusive contamination contribution to indoor air |
mg/m3 |
CL |
Soil gas concentration at source |
mg/m3 |
CL,max |
Saturated vapour concentration |
mg/m3 |
CK |
Convective and diffusive contamination contributions |
mg/m3 |
|
Contamination contribution calculated on the basis of registered soil gas concentration |
mg/m3 |
CM |
Cement content |
kg/m3 |
Co |
Background concentration |
mg/m3 |
Cp |
Soil gas concentration under concrete deck |
mg/m3 |
|
Soil gas concentration measured |
mg/m3 |
CT |
Total soil concentration |
mg/kg |
Cu |
Diffusive contamination contribution to outdoor air |
mg/m3 |
d |
Particle density |
kg/l |
da |
Reinforcement diameter |
mm |
dw |
Crack-determining reinforcement diameter |
mm |
DL |
Diffusion coefficient |
m2/s |
Eb |
Coefficient of elasticity for concrete |
MPa |
Es |
Coefficient of elasticity for steel |
MPa |
fL |
Relative proportion of soil gas contaminant in relation to total content |
unitless |
foc |
Organic carbon content |
relative weight proportion |
h |
Mixing height in atmosphere. |
m |
hb |
Thickness of concrete deck |
mm |
J |
Flux (evaporation) |
mg/m2/s |
Jmax |
Amount adsorbing to the organic fraction of soil particles at equilibrium with saturated solution in water |
mg/kg |
k |
Constant dependent on reinforcement |
unitless |
kb |
Coefficient taking into account influences from composition of concrete |
unitless |
KD |
Soil/water proportion |
l/kg |
kd |
Coefficient taking into account influences from dimensioning |
unitless |
kf |
Coefficient taking into account influences from shrinkage time |
unitless |
Koc |
Organic carbon/water proportion |
l/kg |
Kow |
Octanol/water proportion |
unitless |
l |
Contaminated area length |
m |
lb |
Floor width |
m |
Lh |
Ceiling height of building |
m |
ll |
Floor length |
m |
lm |
Smallest crack spacing in concrete |
mm |
Ls |
Air renewal in building |
s-1 |
ltot |
Total crack length in concrete |
m |
lw |
Average crack spacing in concrete |
mm |
m |
Molecular weight |
g/mol |
MJ |
Actual volume adsorbed to soil particles |
mg/m3 soil |
MJ.max |
Maximum volume adsorbed to soil particles |
mg/m3 soil |
ML |
Actual volume in soil gas |
mg/m3 soil |
ML.max |
Maximum volume in soil gas |
mg/m3 soil |
MV |
Actual volume in soil water |
mg/m3 soil |
MV.max |
Maximum volume in soil water |
mg/m3 soil |
n |
Elasticity modulus |
unitless |
Nn |
Material constant for strata no. n |
unitless |
NJ |
Equivalent material constant |
unitless |
D P |
Pressure differential above concrete deck |
Pa |
p |
Partial pressure |
N/m2 |
pKa |
Acid dissociation constant |
unitless |
Q |
Mass flow velocities |
mg/s |
Qb |
Volume flow through concrete deck |
m3/s |
q |
Volume flow through concrete deck pr. m2 |
m/s |
r |
Equivalent radius of construction |
mm |
R |
Gas constant |
J/mol · K |
RF |
Relative humidity |
% |
S |
Solubility |
mg/m3 |
T |
Temperature |
K |
t0 |
Auxiliary parameter |
unitless |
ts |
Shrinkage time |
days |
v |
Wind velocity |
m/s |
v/c |
Water/cement ratio |
unitless |
VJ |
Relative volumetric proportion of soil particles in soil |
% |
VL |
Relative volumetric proportion of air in soil |
% |
VV |
Relative volumetric proportion of water in soil |
% |
w |
Concrete crack width |
mm |
Xn |
Thickness of diffusion- inhibiting strata no. n |
m |
xJ |
Equivalent thickness |
m |
References
| /1/ | The National Housing and Building Agency, 1992: Diffusionsforsøg,
betongulve (‘Diffusion tests, concrete floors’). [Tilbage] |
| /2/ | The National Housing and Building Agency, 1993: Radon og
Nybyggeri (‘Radon and New Buildings’) [Tilbage] |
| /3/ | Dansk Ingeniørforenings norm for betonkonstruktioner
(‘Danish standard specifications for concrete constructions’) , 1984. Dansk
Standard DS411. [Tilbage] |
| /4/ | Herholdt, A.D., Justesen, C.F.P., Nepper Christensen, P.
& Nielsen, A. 1985: Beton-Bogen (‘The Concrete Book’). [Tilbage] |
| /5/ | Mackay, D. and Paterson, S.: Calculating Fugacity,
Environmental Science and Technology, Vol. 15, No 9, 1981. [Tilbage] |
| /6/ | The Environmental Protection Agency. Project No. 20, 1996: Kemiske
stoffers opførsel i jord og grundvand (‘Chemical substance behaviour in soil and
groundwater’) [Tilbage] |
| /7/ | Baker, P.H., Sharples, S. & Ward I.C.: Air Flow
Through Cracks". Building and environment, vol.22, no.4 1987. Cracks. Building and
Environment, vol. 22, no. 4, 1987. [Tilbage] |
| /8/ | Millington, R.J.: Gas Diffusion in Porous Media,
Science, 130, 1959. [Tilbage] |
| /9/ | Lugg, G.A.: Diffusion Coefficients of Some Organic and
Other Vapours in Air, Analytical Chemistry, 40, 1968. [Tilbage] |