| Front page | | Contents | | Previous | | Next |

Collection Potential for Nickel-Cadmium Batteries in Denmark

3 Assessment of the collection potential

3.1 Assessment methodology
3.2 Handling of uncertainties
3.3 Lifetime assessment
3.4 Update of lifetime distributions for power tools
     3.4.1 Considerations made in previous studies on power tools
     3.4.2 Updates for powertool battery lifetimes for this assessment
3.5 Consumption and defect rates with uncertainty intervals
3.6 Discussion of the hoarding effect
     3.6.1 Taking the hoarding effect into account in calculations
3.7 Illustration of how consumption, lifetime and hoarding effect scenarios affect the collection potential
3.8 Assessment results

3.1 Assessment methodology

The aim of this assessment is to estimate the collection potential of NiCd batteries, i.e. the total quantity of NiCd batteries that could be collected in a given year, if the users dispose of all NiCd batteries through proper collection schemes, and do not discard them with ordinary solid waste etc. This collection potential is here attempted identified on the basis of the following factors:

• Annual consumption (sales quantities) of batteries for the individual applications
• Lifetime of the batteries for each individual application
• The time span in which the users keep defective batteries, before they are disposed of (designated the "hoarding effect").

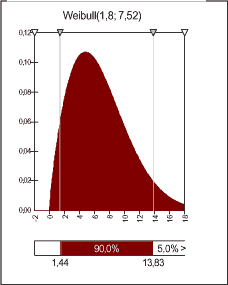
In this chapter the uncertainties of consumption and lifetimes are discussed at first. Thereafter the defect rates are considered (collection potential if no hoarding effect existed). In section 3.6 an assessment of the available knowledge of the hoarding effect is made, and on this background the collection potential of NiCd batteries is estimated.

3.2 Handling of uncertainties

Uncertainty

All data collected/assessed and presented in this report are associated with uncertainty. The uncertainty varies with the quality of the data in question. The uncertainty of each individual input of information is estimated by the authors on the basis of an assessment of the character of the information and the precision of the involved sources.

The term "uncertainty" as it is used in connection with the individual data, is in this report defined as the estimated, maximum uncertainty of the stated information. Uncertainty of data is in the text stated in the form of "A - B" giving the interval limits within which the true value is expected to fall, or in terms of a mean value (or "best estimate") accompanied by an estimated uncertainty on the mean, expressed as a percentages of the mean value. The uncertainty is on other words defined as follows: "A ± B%", where A is the mean value of the parameter, and B is the value for which the true value have the minimal size A - B*A/100%, and the maximal size A + B*A/100% (a normal way of expressing uncertainty on estimates).

Consumption

The calculations of the collection potential for NiCd batteries allows for the inclusion of uncertainties connected with all the input data used for calculating the consumption of batteries.

Battery Lifetime

The information on estimated lifetimes of batteries in the individual applications have been converted to lifetime distributions. Both the stated information of lifetime and the subsequent conversion to lifetime distributions are associated with uncertainty. For resource reasons it was decided not to incorporate the uncertainties of the lifetime distributions quantitatively in the calculation of the collection potential. These uncertainties are instead described on the basis of qualitative considerations combined with a partial sensitivity analysis.

More detailed sensitivity analyses of the impact of the choice of lifetime distributions on the calculated collection potential could be made, given the availability of needed resources.

Hoarding effect

As described in section 3.6 it was decided not to define just one specific time span with associated uncertainties, for the hoarding effect, but instead to assess this effect by creating various scenarios for the possible delay of the disposal of NiCd batteries compared to the annual defect rates.

@Risk

All calculations taking uncertainty into consideration were carried out with the program "@Risk", an "add in" to the Microsoft Excel spreadsheet program. @Risk adds the ability to perform "all" calculations with stochastic variables instead of just constants, that is, calculate on the basis of the "best estimate" of the parameter size and a statistical distribution function expressing the probability of the true value of the parameter falling within any given distance from the "best estimate". @Risk's calculation principle is that instead of for example adding two exact figures, it generates a random figure within the uncertainty distributions of each of the two figures and adds these figures. This procedure is repeated a sufficient number of times to make sure that figures from all "areas" of the two uncertainty distributions have been calculated. The same procedure applies of course, if the figures are included in another calculation than adding, and the number of operations is in principle unlimited. In the calculation made in this assessment 10,000 such iterations have been made - a high end number to ensure best quality estimates. The total calculation result is shown in @Risk as a mean value (which is identical to the calculation result, if the two exact figures had been added) and a probability distribution described on the basis of a number of ordinarily used parameters (quantiles, minimal/maximal value of range etc.).

Uncertainty distribution for consumption estimation

In the calculations carried out in this survey it was chosen to use a so-called histogram function for description of the uncertainty of the data included in the calculation of the sales quantities. The function is designed to be symmetrical around the mean value (the "best estimate"), and there is a relatively higher probability that the "true value" of the figure is closer to than farther away from the mean value. The chosen distribution function type is shown in Appendix B. Regarding these aspects, the distribution principle is similar to the often used Normal distribution (also shown in Appendix B). Contrary to the Normal distribution the chosen distribution function is characterised by the fact that the probability of the true value to be equal to the maximum value (minimum value respectively), has a definite, relatively high value of 50% of the probability of the true value being equal to the mean value. This is the case irrespective of the current maximum uncertainty of the information in question. This distribution is chosen as a reasonable reflection of the way "uncertainty" has been interpreted in this assessment. Other uncertainty distribution functions could have been used, and technically, it is straight forward to implement other functions instead.

In the figures in Appendix B it is shown how the distribtuion function looks for data with an uncertainty of ± 20% and ± 50% of the mean value respectively. For comparison the density function of an Normal distribution with a standard deviation of 20% of the mean value is also shown in the appendix. In Appendix B the parameters of the chosen histogram function are shown.

3.3 Lifetime assessment

The following section described how lifetime data were collected, interpreted and applied in the methodology developed by Maag and Hansen (1994). Detailed discussions of application patterns and lifetime estimates were given by Maag and Hansen for all major NiCd battery uses. The discussions have not been reflected here except for the resulting lifetime estimates presented in Appendix A. An example of the discussions is however given for power tools in section 3.4 as part of the update of the lifetime estimates for power tools for this assessment.

Lifetime data

The interviewed sources of the information on lifetimes of batteries for the different applications have in most cases been able to provide information on what they considered the minimal lifetime, the mean lifetime and the maximal lifetime of the batteries.

The minimal lifetime is for most applications expressed indirectly as the percentage of the batteries that became defective within the typical period of guarantee of 1 year.

The mean lifetime must be considered the typical lifetime of the majority of the batteries for the application in question.

The maximal lifetime must be considered the longest lifetime the sources have experienced or can imagine by projecting their other experience of battery lifetimes.

It is emphasized that in all cases the figures are estimates, and the estimates were made with varying uncertainty. The lifetime information shown in Appendix A and (Maag and Hansen, 1994) is however substantiated by the authors' own assessments based on knowledge of the application pattern of batteries for the application in question and general knowledge of the reasons for NiCd battery defects.

Lifetime distributions

The estimates of lifetimes stated in Appendix A have been "converted" into continuous lifetime distributions in order to obtain a continuous picture of the tempo at which a given quantity of batteries become defective.

As the actual calculations are related to whole years, it has however been necessary to "convert" again the continuous distribution to a discretionary annual distribution. That is to say, based on the continuous distribution the percentage of batteries becoming defective in each individual year of the total lifetime has been calculated.

It was chosen to use the so-called Weibull distribution function as the continuous distribution being the central link in the interpretation of the collected data on battery lifetimes. Figure 3.1 shows the distribution function of a Weibull distribution, here an example with the parameters (aá;ß) = (1.80;7.52).

Figur 3-1 Density function of a Weibull distribution with (aá;â) = (1.80;7.52).

The data basis (minimal, mean and maximal lifetimes) in itself is not detailed enough to rule out that there might be other statistical distributions that could describe the lifetimes of batteries better than Weibull distributions, but the Weibull distribution is chosen here as a suitable type of distribution for the following reasons:

• Weibull distributions with form parameter above 1 have natural minimum in the value 0, i.e. the distribution does not assume negative values (contrary to e.g. the Normal distribution)
• For Weibull distributions with form parameter above 1 the probability of the occurrence (here defect = the "death" of the battery) taking place close to the typical lifetime rather than far from it is much greater (the distribution is much closer around the typical lifetime than in the "tails", see figure 3.1). This is very much like the Normal distribution
• The Weibull distribution might be asymmetrical. For most applications of NiCd batteries this means that the distribution is able to describe very high maximal lifetimes compared to the typical lifetime for the application in question (because of very extensive use of the battery)
• The Weibull distribution is often used to describe lifetimes of appliances, appliance components and the like.

Parameter estimation

The parameters for the applied Weibull distributions were found on the basis of the assessed minimal, mean and maximal lifetimes for each battery application at regression to the "least squares method" (commonly used for this purpose).

Deviations from Weibull

Generally it has been possible to find Weibull distributions corresponding well to the estimated lifetime data. However in approximately half the lifetime distributions it has turned out that the Weibull distribution underestimates the number of batteries that becomes defective within the 1-year period of guarantee. It these cases it was chosen to adjust the used Weibull distribution in such a way that the best possible adjustment to the estimated lifetime data is achieved. The chosen lifetime distributions for the various applications are shown in Appendix A.

Uncertainty of lifetime distributions

The lifetime information provided in Appendix A is as it appears associated with an uncertainty that can be significant. Nevertheless the lifetime information is considered to indicate the overall tendencies of the lifetime of NiCd batteries in the applications in question. As the uncertainties of the lifetime information mentioned in Appendix A are not incorporated quantitatively in the collection potential calculations, the impact of these uncertainties on the final results of the calculation is attempted described here by the following considerations.

If the true lifetime conditions deviate from the "best estimate" made in this report, it might be reflected in the following ways:

1. The true typical mean lifetimes might be lower or higher than the estimated lifetimes. This would mean that the majority of a quantity of batteries taken into use at a given time becomes defective before or after the estimated time respectively, i.e. there would be a certain time deviation in time.
2. The range of lifetimes of the individual batteries might be wider or narrower than assessed. This means that a quantity of batteries taken into use at a given time becomes defective over a longer or shorter period of time than assessed.
3. A combination of the above two considerations.

In order to provide an insight into the importance of such possible deviations to the calculated total quantities of defective batteries, the defect rates and the collection potential of NiCd batteries in sections 3.5 and 3.6.2, respectively, are determined on the basis of three different lifetime distributions for professional battery-powered tools, which is clearly the most important individual application of NiCd batteries. The applied lifetime distributions are all within the estimated uncertainties on the lifetime information on professional power tools.

3.4 Update of lifetime distributions for power tools

3.4.1 Considerations made in previous studies on power tools

This section describes the considerations originally made on lifetime for NiCd batteries for power tools by Maag and Hansen (1994). They reflect the data use pattern, battery and charger characteristics available at that time, and give an example of how Maag and Hansen assessed the lifetime of NiCd batteries for specific uses. A 2004 update of the lifetime data for professional and do-it-yourself power tools is given in section 3.4.2 below.

Application pattern

As to application pattern a distinction must be made between professional and "do-it-yourself" (DIY) users.

Professional users

The professional user must have certainty of reliability at any time. Consequently there are two battery packages for each machine, and the battery packages are charged by turns. As the operating time is short per charging, each battery will at intensive work be charged up to several times a day. It is assumed that professional users on average carry out one charging a day, corresponding to one charging of each individual battery every other workday.

For professional users especially overloading during discharging (pole reversing and heat build-up), widespread use of high-speed chargers, mechanical damage and leaking of electrolyte are deemed to influence the lifetime of the batteries.

DIY users

Do-it-yourself users are considered to generally use the machine far less intensively. It is however assumed that the DIY user of a battery-driven power tools is using the machine more often than the average user, who will often have a somewhat cheaper machine for line voltage. On the basis of information from several users it is assessed that the batteries are typically charged 1 to 5 times a month on average. It is estimated that mechanical damage will be less important in connection with DIY machines. According to information from importers, the batteries in DIY machines are of similar quality to those in the professional machines. Other conditions as to the lifetime are assessed to correspond to those of the professional machines.

Lifetimes

The maximum lifetimes in cycles was estimated by Maag and Hansen (1994) at 800 - 1000 cycles with the use of the most widespread high-speed chargers. The average lifetime was estimated at 300 - 500 cycles.

The lifetimes expressed in number of years shown in table 3-1 were estimated on the basis of information from suppliers and distributors and the above comments on charging frequency and battery lifetimes in cycles. Please note that for professional machines the parallel use of two battery packages charged by turns is assumed. The estimated uncertainties are based on the variations among individual data.

Table 3-1 Estimated lifetimes expressed in years for batteries in professional power tools.

Notes:

*1 The 10% of the batteries that are exhausted fastest. The lifetime stated in this row is thus the time in which 10% of the battery packages are considered defective

*2 Is considered the 98% quantile. The lifetime stated in this row is thus the time in which 98% of the battery packages are considered defective

*3 At parallel use of 2 batteries charged by turns. Argumentation appears from the text.

3.4.2 Updates for powertool battery lifetimes for this assessment

The lifetime estimates were checked and updated for professional and do-it-yourself power tools in this study (2004) because of their dominating influence on the total NiCd consumption and thereby the collection potential.

For a number of the dominating quality brands of professional and do-it-yourself powertool brands, persons in charge of the brands central repair shops were contacted and interviewed on their experience of lifetimes for NiCd-powered tools. The interviewed persons had between 8 and 13 years of experience with repairs and guarantee-reclamations for the brands in question, and appeared qualified to evaluate trends in lifetime data for these products.

The interviewed persons preferred to express their experience on battery lifetimes in terms of years. Some of them did indicate that though the main principles of the battery charger technology were the same as in 1994, slight improvements may have been made on chargers, possibly indicating increased average numbers of cycles for NiCd batteries in power tools. On the other hand, the experience base with NiCd powered tools have grown, and any potential increases in number of charging cycles did not result in changes in average mean lifetimes as compared to the 1994 study.

Minimal lifetimes

Some of the interviewed persons expressed that minimal lifetimes - expressed as the number of defective batteries within 1 year of purchase - had been higher in the mid 1990's, (due to too weak electro-motors resulting in reclamations), than today, both for professional and do-it-yourself power tools. Minimal lifetimes have been adjusted correspondingly here (see table 3.2).

Mean lifetimes

All interviewed persons agreed to the mean lifetimes concluded in the 1994 study.

Maximum lifetimes

The interviewed persons' estimates for maximum lifetime for professional power tools varied somewhat - perhaps indicating differences between the brands - but on the average this did not result in a need to change the maximum lifetime estimate for professional power tools.

For do-it-yourself power tools however, all persons meant that the maximum lifetime was lower today than estimated in the 1994 study (to a varying degree). The maximum lifetime for batteries for do-it-yourself power tools has correspondingly been lowered 2 years as shown in table 3.2.

Updated lifetime distributions

Updated lifetime distributions were chosen in accordance with the data given in table 3.2. Both distribution functions are discretionary annual distributions based on Weibull distributions but adjusted to account for defect rates due to reclamations during the first year after purchase. The updated distribution functions are shown in Appendix A.

In the calculations of the collection potentials, the original 1994 lifetime distributions were used for power tools consumption in the years 1985-1993, whereas the updated lifetime distributions were used for consumption in years 1994 through 2004.

Table 3-2 Estimated lifetimes expressed in years for batteries in power tools.

Notes:

*1 Is considered as the 98% quantile. The lifetimetime stated in this row is thus the time in which 98% of the battery packages are deemed defective

*2 At parallel use of 2 batteries charged by turns. Argumentation appears from the text.

3.5 Consumption and defect rates with uncertainty intervals

Consumption

In table 3.3 the total annual sales quantities of NiCd batteries for each year of the period 1985 - 2002 are shown with uncertainty intervals, as calculated with the use of stochastic variables in @Risk. The same data are shown graphically in figure 3.1

The uncertainties are presented as 5%/95% quantiles, which state the interval limits within which 90% of the calculated results of the computer simulation fall. Seen statistically, there is a high probability that the "true" value of the consumption in the individual years lies within the interval indicated by these quantiles. Correspondingly, the probability of the "true" value being outside this interval must be considered negligible.

Table 3-3 Total annual sales quantities of NiCd batteries in tonnes shown with calculated uncertainty intervals

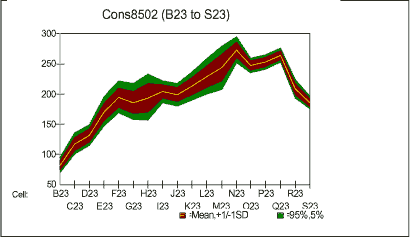
Figure 3-1 Total annual sales quantities of NiCd batteries shown with calculated uncertainty intervals (1985 at left to 2002 at right); tonnes/y

Note: X-axis notation refer to spreadsheet cell numbers; actually representing years from 1985 (B23) to 2002 (S23). Outer rims of green shade represent 5% and 95% quantiles. See numbers in table 3.3 above.

Calculated defect rates

The calculated defect rates of NiCd batteries not including the hoarding effect are shown in table 3.4 below.

Note that to enhance the application of the collection potential assessment, consumption forecasts for 2003 and 2004 have been included in the calculations of the collection potentials. Consumption in 2003 and 2004 (and associated uncertainties) are counted as equal to the estimated consumption (and uncertainties) in 2002 for all uses. This may be a minor overestimation, as the consumption trend may be declining. Further improvement of the forecasts are technically possible, but have not been attempted due to budget restraints.

Investigation of sensitivity of defect rates to choice of lifetime distribution

Besides the calculation of the "best estimate" defect rates, an assessment was made to illustrate the sensitivity of the total defect rates to choice of lifetime distributions. The results of which are also shown in table 3.4. This was done by carrying out three sets of calculations, only differing from each other by the use of 3 different lifetime distribution for batteries sold for professional power tools. The applied lifetime distributions for professional power tools can be characterised as follows:

• "Best estimate" is based on the lifetime distribution considered most realistic to professional hand tools. Lifetime parameters (see explanation in table notes section 3.4.): -1993: Min: 10% in 1st year/Mean: 4 years/Max: 6years; 1994-2004: 4%/4y/6y.
• "Shorter lifetime" corresponds to the assumption that mean lifetime and maximal lifetime of professional hand tools are shorter than that of the best estimate. Lifetime parameters (see explanation in table notes section 3.4.): 1986-2004: Min: 10% in 1st year/Mean: 2-3 years/Max: 5 years.
• "Longer lifetime" corresponds to the assumption that mean lifetime and maximal lifetime of professional hand tools are longer than that of the best estimate.. Lifetime parameters (see explanation in table notes section 3.4.): 1986-2004: Min: 3% in 1st year/Mean: 5 years/Max: 7 years.

Table 3-4 Calculated total battery defect rates (all uses), and sensitivity to 2 other tested options for lifetime distributions for professional power tools; tonnes/y.

The relevance of assessing the importance of the lifetime distribution on the basis of professional hand tools is based on the dominant significance this field of application has had to the total sales of NiCd batteries in the major part of the period 1985 - 2002. The sales of batteries for professional power tools have constituted approx. 78% of the total sales in 1985, declining to approx. 24% in 1993, and again rising to about 50% in 2002.

Table 3.4 also show the calculated 5% quantiles and 95% quantiles, similarly to table 3.3 above. As shown, the calculated battery defect rates are quite robust to the tested choices of lifetime distribution. This is of course partly due to the fact that professional power tools do not constitute the total sales of NiCd batteries, but also because all tested lifetime distributions have a "smoothing" effect , distributing anticipated battery defectives over a range of years (not all batteries bought in "year 1" become defective within the same "year x"; see illustration in section 3.7).

More detailed sensitivity analyses of the impact of the choice of lifetime distributions on the calculated collection potential are technically possible, provided the needed resources are available.

3.6 Discussion of the hoarding effect

The term "hoarding effect" is used here as designation for the phenomenon that users of NiCd batteries keep defective batteries for a certain period of time, before they are delivered to a collection system or disposed of in another way. This behaviour will of course affect the collection potential.

To the authors' knowledge no surveys providing reliable knowledge of the hoarding effect for NiCd batteries in Denmark or other topics applicable as a measure for such batteries have been carried out. Also two recent studies related to battery collection in Denmark have been studied (Hansen and Hansen, 2003; Husmer et al., 2003), and no information was found that give reason to change the hoarding effect scenarios used here. An assessment of the hoarding effect in Denmark (or in a comparative study in selected European countries) could be useful to minimise uncertainties on the calculated collection potentials, but have been beyond the scope of the current assessment.

For these reasons it was decided to include the hoarding effect in the assessment through the scenarios developed by Maag and Hansen (1994). In the following a description of the actual knowledge available on the hoarding effect is initially given.

Experience with primary alkaline cells

(Text adapted from Maag and Hansen, 1994). As part of the Danish EPA's efforts of surveying the contents of mercury in alkaline cells, the Danish EPA has for the years of 1990, 1991 and 1992 on a spot-checking basis measured the contents of mercury in new alkaline cells for sale in Danish shops as well as in used alkaline cells received by the national hazardous waste handling company "Kommunekemi". The spot check included each year 50 new and 50 used batteries. Additionally, measurements of the mercury content in used batteries (spot check of 50 batteries) received by Kommunekemi in 1993 were carried out (data are presented in detail by Maag and Hansen (1994)). As in the period from 1990 to 1993 there was a significant decline of the mercury content in these batteries, and therefore these data have made it possible to obtain a certain impression of the hoarding effect of alkaline cells:

• A minor part (approx. 20%) of the total quantity of alkaline cells collected was received by Kommunekemi only one year after they were sold.
• A minor part (20-25%) of the total quantity of alkaline cells collected were received by Kommunekemi at a delay of 3 years or more compared to the year in which they were sold.
• As to the remaining part of the batteries (i.e. the majority) it seems there is a delay of 2 years, calculated as the difference between the time from the batteries were sold till they were received by Kommunekemi.

Assuming that the consumers buy the batteries as required and that the lifetime of alkaline cells in use is normally shorter than one year (lifetimes of 2-3 years are known, but these cover probably only a marginal part of the consumption), it can on the basis of these results be assessed that for alkaline cells, the average hoarding effect was 1-2 years.

For a minor part of the batteries the hoarding effect will however be two years or more. The best estimate of the size of this part is 20-25% of the total quantity. This assessment is however very uncertain, and the survey results do not allow a sharper precision than the following formulation: The part is somewhere within the interval of 10 - 50%.

Selected examples

(Text adapted from Maag and Hansen, 1994). As part of their study, Maag and Hansen performed a minor spot-checking investigation. This investigation included interview/filling in a questionnaire with/by a small group of persons who had all for private use acquired NiCd batteries and/or equipment containing such batteries. Additionally the persons were characterised by belonging to the Danish Association for collection of rechargeable batteries, or by being colleagues, neighbours or friends of the authors of the assessment.

The results of the investigation can be resumed as follows:

• In total, interviews were carried out/questionnaires received from 27 persons whose household used or had used NiCd batteries.
• Of these persons 8 persons had had NiCd batteries or equipment containing such batteries which became defective.
• Of the 8 persons who had discarded batteries or equipment, only 2 persons had actually disposed of batteries/equipment, whereas the other 6 persons were still keeping the batteries/equipment (hoarding effect).
• The persons still keeping the batteries had at that time typically kept the batteries for more than 2 - 4 years. One person had only kept them for approx. 1 year, whereas another person had kept them for more than 13 years (an old battery from a pocket calculator).
• Of the two persons who had actually disposed of their batteries, one had disposed of them according to the regulation, whereas the other person had thrown them into an ordinary waste container (two vacuum cleaners - the person did not realise that these contained rechargeable batteries).
• It was noted that the person who discarded the vacuum cleaners, still keeps a defective battery for a mobile phone installed in his car, as the phone functions on the car battery, although the NiCd battery is defective. The NiCd battery had then been defective for approx. 2 years, but was still in its place on the mobile phone.
• All 27 persons using or having used NiCd batteries, know in principle how such batteries are to be disposed of (all persons were, when the question was asked, able to mention one or more possibilities of how to dispose of the batteries in a safe way).

The results of this spot-check investigation must of course be taken with reservations because of the modest extent of the investigation. The fact that 6 out of 8 random persons (in reality 6.5 out of 8 persons) in one way or the other keep discarded batteries, is however expressing a clear tendency to which a certain weight should be attached.

Interview investigation on NiCd batteries

(Text adapted from Maag and Hansen, 1994). On behalf of the Association for collection of rechargeable batteries (Foreningen for indsamling af genopladelige batterier), AIM Research in February 1994 carried out a phone interview investigation, in which a total of 509 households were contacted by phone and answered questions about rechargeable NiCd batteries. Of these households 230 households had rechargeable batteries or equipment containing such batteries. Another relevant result of the investigation was that approx. 17% of the 230 households kept batteries that did not function, but were not yet disposed of.

Collection from businesses

In this project no interviews has been aimed directly with businesses. On the basis of COWI's general experience with businesses and their environmental conditions it is assessed that in most Danish businesses collection and disposal of NiCd batteries would normally be systemised (discarded batteries to be disposed of at a certain place, kept in a box; when the box is full, it will be taken to the local receiving station for chemical waste - the responsibility lies with a certain employee). This means that at such businesses no hoarding effect longer than the time it takes to fill up the box can be expected (typically from a couple of months to one year).

3.6.1 Taking the hoarding effect into account in calculations

There is no doubt that a hoarding effect is existing for consumers of NiCd batteries as well as other batteries, and that this effect in all probability has an extent that could have substantial impact on the collection potential of NiCd batteries.

The mechanisms behind this hoarding effect are considered to be the following:

• The innate desire of many persons to keep things that are defective and might as well be discarded. This desire of keeping things must in reality be considered a characteristic with many persons and is actually only limited by the space available in their residences and the extent to which possible other members of the household have the same desire
• Knowledge of NiCd batteries being environmentally harmful and consequently must be disposed of in a special way (i.e. not in the waste container) combined with the fact that it typically requires a special effort to dispose of these batteries (collect the defective batteries, put them in a plastic bag and remember to take them to the nearest receiving station when in the neighbourhood next time, might to a number of persons be a task that has low priority, as long as the batteries do not require too much space).

The extent of the hoarding effect is however difficult to determine precisely. Consequently it was chosen here to illuminate the importance of the hoarding effect by means of a number of scenarios as described in the following.

The background of these scenarios is that it is distinguished between "well-organised users" and "disorganized users".

Well-organised user

A well-organised user is here defined as a user who has established well-functioning routines for keeping and disposal of NiCd batteries. This will typically be the case with a number of large businesses - especially businesses that have introduced or are considering the introduction of quality assurance routines. A large number of small businesses that are generally characterised by a good sense of order are also expected to deserve this designation.

For well-organised users the hoarding effect is expected to be up to one year, but hardly much longer.

Disorganized user

Contrary to the above, an disorganized user is considered a user who has no well-functioning routines for handling of batteries. This is expected to be the case for largely all private users and also a considerable number of small businesses.

It is to be expected that for disorganized users generally hoarding effects of several years can be foreseen. This does however not rule out that also disorganized users will dispose of batteries with no significant delay. But it is among the disorganized users that the significant hoarding effect is to be found.

Who uses what

A crucial question is now how the use of NiCd batteries for different purposes can be distributed on well-organised users versus disorganized users. It has been chosen to assume the following:

Professional power tools: This type of equipment will be used by well-organised users" as well as disorganized users. A rough assessment is a 50%/50% distribution.

DIYpower tools: It is assumed that this type of equipment is used exclusively by disorganized users.

Hand-portable mobile phones: Until the early 1990's the price of these phones has been so high that it has mainly been equipment financed by businesses. A number of businesses belong however to the category disorganized users. A rough estimate is a 50%/50% distribution on well-organised versus disorganized users. This distribution may likely have changed towards more private users by the mid 1990's, but for simplicity this has not been changed in the hoarding effect scenarios.

Cordless phones: In the early and mid 1990's, this type of equipment was mainly purchased by businesses. This assumption may have changed towards more private users in the mid/late 1990's. A rough estimate is a 50%/50% distribution on well-organised versus disorganized users.

Portable phones: When used (mainly till the mid 1990's), this type of instrument was mainly used by businesses, and the battery was, if necessary, normally exchanged by the supplier. A rough estimate is that this type of equipment was exclusively used by well-organised users.

LMR radio communication equipment: This type of equipment is mainly used by a well-defined circle of users (police, military, Falck's life-saving service and private protection agencies) that must be assumed belonging to the well-organised users.

Portable computers: NiCd-powered computers were mainly bought by businesses. A number of businesses belong however to the category disorganized users. A rough estimate was a 50%/50% distribution on well-organised versus disorganized users.

Camcorders, individual battery cells sold to consumers, equipment for households and personal care: This was equipment mainly bought by disorganized users.

Other: This was equipment mainly bought or serviced by professional personnel. It is assumed that this type of equipment was used by well-organised users.

Scenarios

The chosen scenarios are as follows:

Scenario 1: For well-organised users the hoarding effect is 1 year. For disorganized users the hoarding effect is on average 2 years.

Based on the available knowledge of hoarding effect this scenario is from the outset considered a scenario that might be realistic, but probably will tend to underestimate the hoarding effect with the disorganized users.

Scenario 2: For well-organised users the hoarding effect is 1 year. For disorganized users the hoarding effect is on average 4 years.

Based on the available knowledge of hoarding effect this scenario is from the outset considered a scenario that might be realistic.

Scenario 3: For well-organised users the hoarding effect is 1 year. For disorganized users the hoarding effect is on average 7 years.

Based on the available knowledge of hoarding effect this scenario is from the outset considered a scenario that could likely overestimate the hoarding effect.

Scenario 4: For well-organised users as well as disorganized users the hoarding effect is an average 4 years.

Based on the available knowledge of hoarding effect this scenario is from the outset considered a scenario that could likely overestimate the hoarding effect.

3.7 Illustration of how consumption, lifetime and hoarding effect scenarios affect the collection potential

The relationship between consumption, battery defect rate and collection after the hoarding effect is shown for an example, professional power tools, in figure 3-2 below. It should be noted that the figure is only meant to illustrate the principles applied in the assessment, and discussion of the numbers themselves are given in other sections of the report.

The blue line is the estimated consumption of NiCd batteries in the assessed period. The consumption peaked in 1988 and 2000. The consumption before 1985 and after 2004 was not estimated. As such, the figure illustrates in principle how the situation would be if sales of this NiCd application did not continue after 2004.

The pink line illustrates how the defect rates are delayed compared to the consumption. The peak defect rates are observed after about 1 average lifetime after the consumption peaks. The defect rate peaks are wider than the consumption peaks because the lifetime distribution applied spreads the battery defect incidents over a range of years around the average lifetime, reflecting the fact that not all batteries becomes defective at exactly the same time after purchase. The defect rates before 1990 are not shown, because the input consumption estimates before 1985 are not available.

Click here to see figure 3-2

The yellow line is the calculated annual collection potentials. It illustrates how the hoarding effect further delays the actual discarding of the defective batteries. In this case, the collection potential under hoarding effect scenario 3 is shown. In this scenario, half of the consumption of professional power tools is assumed used by so-called "organised users", who discard their defective batteries 1 year after defect on average, while the other half is assumed used by "un-organised users", who discard their defective batteries 7 years after defect on average. The discarding time is delayed in time compared to the time where the battery becomes defective, and the compound hoarding effect model used, further spreads the discarding of the consumed batteries over time. If scenario 4 had been used, the yellow line would be a precise replica of the defect rate line (pink line), but would simply be delayed 4 years, compared to the defect rates.

3.8 Assessment results

The assessment results of the above scenarios are presented in table 3.8 below. This table shows for each scenario the calculated mean values (bold red) of the collection potentials, and the 5% quantiles and the 95% quantiles representing the value between which 90% of the simulation results fall. Besides this, the table shows the 5% and 95% quantiles from the calculations of the "shorter lifetime" option for professional power tools (discussed in section 3.5), denoted as S-5% and S-95%, and corresponding quantiles for "longer lifetime" option, denoted as L-5% and L-95%. For the years 2000-2005, the minimum and maximum of all quantiles shown for each scenario are marked in bold.

Note that to enhance the application of the collection potential assessment, consumption forecasts for 2003 and 2004 have been included in the calculations of the collection potentials. Consumption in 2003 and 2004 (and associated uncertainties) are counted as equal to the estimated consumption (and uncertainties) in 2002 for all uses. This may be a minor overestimation, as the consumption trend may be declining. Further improvement of the forecasts are technically possible, but have not been attempted due to budget restraints.

A closer look at the results in table 3.8 reveals that the resulting collection potentials are rather robust to both the hoarding effect scenarios, and the different lifetime options tested, for the period 1997-2005, which is of most interest here. This is considered mainly a result of the consumption trends in the years influencing the values most, in combination with the "smoothing" effect of the battery lifetime distributions (not all batteries bought in "year 1" become defective within the same "year x", see illustration in section 3.7). As shown in section 2.9, the consumption peaked in the years 1997-2000 and exhibits a declining trend from 2000 to 2002.

Table 3.5 show the mean collection potential values, as well as the absolute minimum and maximum among the presented quantiles, across all 4 scenarios. The table also show the calculated differences between minimum and maximum quantiles for each year in tonnes, and half of the same difference in percent of the mean value.

Table 3-5 mean collection potential values, as well as the absolute minimum and maximum among the presented quantiles, across all 4 scenarios, in tonnes/y. Calculated differences between minimum and maximum quantiles for each year expressed in tonnes, and half of the difference in percent of the mean value.

Note *1: Minimum and maximum among all quantiles across all four hoarding scenarios and all three lifetime options tested. *2: An alternative presentation of the uncertainty on the mean, e.i. the distance between the mean value and the interval limits. The numbers in the column express the "A" in the often used notation "Mean +/- A %".

Conclusions

Though the assessment made do not fully include all associated uncertainties, it may be concluded that there is a high likelihood that the true collection potentials for NiCd batteries in Denmark fall between the min and max values shown in table 3.5.

For comparison, the collected amounts of NiCd batteries in Denmark each year since the introduction of the state-paid awards for collected NiCd's in 1996 are shown in table 3.6.

Table 3-6 Collected NiCd batteries registered in Denmark 1996-2003, tonnes/y (Danish EPA, 2004)

Note that some time passes between the NiCd batteries are originally collected and the time when the awards are paid and the amount therefore can be seen in the Danish EPA's statistics (so-called "pipeline effect"). In line with normal business principles, this time does most not likely exceed 1 year. The collection award was 120 DKK/kg NiCd batteries collected from 1996-1999, but was raised to 150 DKK/kg as from 2000. The award is the main driver behind this controlled system, and the numbers presented may be considered as precise.

When comparing the data in the two tables, the overview shown in table 3-7 emerge. Note that here, the collected amounts presented for 1997 are the amounts registered in 1998, to account for the pipeline effect. The table shows that the estimated collection potentials indicate that large amounts of NICd batteries have been collected, but a more or less equal part of the potential has not been collected.

Table 3-7 Comparison between estimated collection potentials and actually collected NiCd battery amounts

Click here to see table 3-8

| Front page | | Contents | | Previous | | Next | | Top |

Version 1.0 May 2005, © Danish Environmental Protection Agency