Følgevirkninger af råstofgravning under grundvandspejlet
4. Grundvandssænkning som følge af vådgravning
4.1 Opstilling af ligninger
Problemet, der skal løses, er vist skematisk på Figur 4.1. Det er valgt at løse
ligningerne i rotationssymmetri, idet dette dels giver væsentlige matematiske fordele,
men tillige er en cirkulær grav en passende praktisk tilnærmelse til en grav, som har
horisontal tilstrømning fra alle sider, og hvis sider har nogenlunde samme længde.
Tilnærmelsen vil altså være dårligere, jo mere langstrakt graven er.
Grundvandsmagasinet har uendelig horisontal udstrækning og befinder sig i området 0 <![]() <H, hvor H er den vandmættede højde inden gravningen starter.
Grundvandsmagasinet regnes homogent og isotropt med hydraulisk ledningsevne Kh.
Transmissiviteten er T=Kh·H.
<H, hvor H er den vandmættede højde inden gravningen starter.
Grundvandsmagasinet regnes homogent og isotropt med hydraulisk ledningsevne Kh.
Transmissiviteten er T=Kh·H.
| Den effektive porøsitet er | , 0< | <1 |
| Der ses bort fra den vandmængde, der fjernes fra søen sammen med det opgravede materiale. Gravningen starter til tiden t=0 og foregår på en sådan måde, at der graves en konstant råstofmængde pr. tidsenhed, og der graves over hele højden H. Arealet af søen i graven vil derfor vokse | |||
| lineært med tiden og radius rf (t) af søen med
|
|||
Sænkningen af søens vandspejl hf (t) er lig med sænkningen h(r,t) i grundvandsmagasinet ved skillefladen.
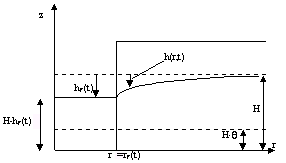
Figur 4.1
Skematisk illustration af vådgravning.
Strømningsproblemet beskrives ved hjælp af en styrende differentialligning med tilhørende begyndelses- og randbetingelser. For en detaljeret beskrivelse af ligninger og løsning henvises til Bilag A.
Differentialligningen lyder
(4.1) |
| hvor | (m2/s) er diffusiviteten. |
| Her er benyttet tilnærmelsen |
Begyndelses- og randbetingelse er
(4.2) |
Sænkningen i søen og i grundvandsmagasinet skal være ens ved skillefladen:
(4.3) |
Dette gøres ved hjælp af en global vandbalance
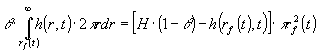 |
(4.4) |
I ligning (4.4) udtrykker venstre side den vandmængde, der er fjernet fra grundvandsmagasinet, mens højre side er et udtryk for det nettovolumen, der er fjernet fra graven, se nærmere beskrivelse i Bilag A.
For at ligningerne skal kunne løses, er det nødvendigt at specificere gravebetingelserne og dermed rf (t). Det antages, at det udgravede volumen er konstant pr. tidsenhed, og at gravningen starter ved r = 0. Dette resulterer i ( se Bilag A)
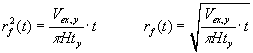 |
(4.5) |
| Her er | (m3) det udgravede | ||
| volumen inden for | en given tidsperiode | ||
| (for eksempel 1år). | / | er således gravehastigheden. |
| Det udgravede volumen vokser lineært med tiden, hvilket betyder, at | |
| bliver proportional med kvadratroden af tiden. |
| Introduceres den dimensionsløse konstant: |
(4.6) |
|
| fås ved at kombinere (4.5) og (4.6): |
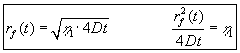 |
(4.7) |
| Parameteren |
|
er kvadratet på forholdet |
| Nævneren | er et mål for det område i grundvandsmagasinet, |
| inden for hvilket der sker sænkninger til tiden t under graveprocessen. Dette udtryk er velkendt fra teorien fra grundvandsstrømninger omkring en boring. | ||
| En lille værdi af | betyder, at det påvirkede område er stort i forhold til | |
| radius af det udgravede område. | ||
| Ligningssystemet til bestemmelse af | er nu: |
(4.8) |
(4.9) |
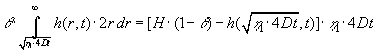 |
(4.10) |
4.2 Analytisk løsning
| Løsninger til (4.8) er ofte en funktion af parameteren |
Der søges derfor en løsning af formen
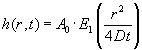 |
(4.11) |
| Her er | det det såkaldte eksponentielle integral |
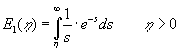 |
(4.12) |
| Fra teorien om pumpning fra boringer er det eksponentielle integral også kendt som "boringsfunktionen", der indgår i Theis’ formel. Løsningen ses let at opfylde (4.8) – (4.9). Faktoren |
|
| skal bestemmes ved indsættelse i (4.10) | |
| . Efter en del regning som er beskrevet i Bilag A findes | |
(4.13) |
Den endelige løsning findes ved at indsætte (4.13) i (4.11),
| (4.14) |
Her er indført en ny funktion, som passende kan benævnes et modificeret eksponentielt integral:
(4.15) |
Funktionens graf er vist i Bilag A.
4.2.1 Vandspejlet i råstofgraven
| Sænkningen, | af vandspejlet i råstofgraven findes ved | |
| indsættelse af (4.3) og (4.7) i (4.14): | ||
(4.16) |
Der fremkommer det overraskende resultat, at sænkningen er uafhængig af tiden. Det betyder, at gravningen bevirker en momentan sænkning af vandspejlet i graven, og herefter holder sænkningen sig konstant.
| Den første faktor i løsningen |
| er den maksimale sænkning, der kan opnås, og den opstår ved, at der ikke |
| strømmer vand ind i graven under graveprocessen. Det svarer til, at |
| vandhøjden i graven er |
(4.16) kan simplificeres ved at rækkeudvikle det eksponentielle integral og kun beholde betydende led. Dette er vist i Bilag A. Resultatet er:
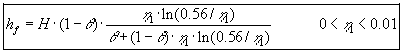 |
(4.17) |
Fejlen, der begås ved at benytte denne formel er mindre end 1% i det angivne interval
og mindre end 5% for ![]() .
.
4.2.2 Vandspejlet i grundvandsmagasinet
| Sænkningen i grundvandsmagasinet, |
afhænger af r og t på en relativ enkel måde. Af (4.14) fås:
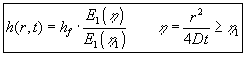 |
(4.18) |
| Sænkningen i selve graven , | er givet af (4.16) eller approximationen | ||
| (4.17). Værdien af h er lig | med | for |
|
| varierer h som . |
|||
Figure 4.2 viser grafen for ![]() og funktionens asymptoter for for små og store værdier af
og funktionens asymptoter for for små og store værdier af ![]() . For små og store
. For små og store ![]() har funktionen følgende asymptoter (Abramovitz og Stegun, 1964):
har funktionen følgende asymptoter (Abramovitz og Stegun, 1964):
- |
(4.19) |
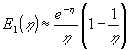 |
(4.20) |
| Tallet 0.577 er Eulers konstant ( | |
| Fejlen ved at benytte approximationen (4.19) | |
| er mindre end 1% for | mindre end 0.002% for |
| og lig to 9% for | De to første led, | ||
| vil normalt være tilstrækkelige for |
|||
| Den ret grove approximation | (4.20) |
| tilnærmer | for store argumenter. Den relative fejl er mindre end 12% |
| for |
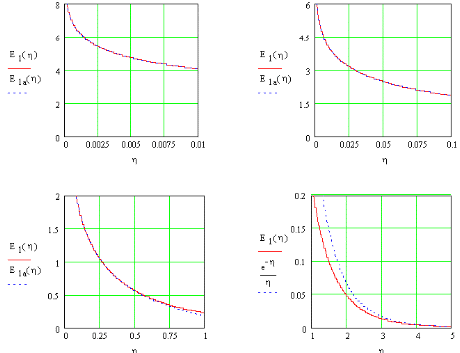
Figur 4.2.
Det eksponentielle integral![]() (4.12) og dets asymptoter (4.19- .20).
(4.12) og dets asymptoter (4.19- .20).
4.2.3 Praktisk eksempel
Landberg (1982) præsenterer data fra starten af grusgravning ved Örsjö i det sydvestlige Skåne. Der er gravet i tre perioder med måling af vandspejlsændringer i en boring, som er placeret i kanten af søen. Om boringen har en egentlig afstand til søen, og hvad den i givet fald er, vides ikke. Vandspejlsændringerne som funktion af gravning og nedbørshændelser er vist i Figur 5.3.
Det ses, at der er en hurtig respons på nedbøren, men også at gravningen giver omgående respons. Der er gravet i tre adskilte perioder, og gravningen giver tilsyneladende anledning til størst sænkninger i den første periode, hvor der ikke er en eksisterende råstofsø, som kan dæmpe sænkningerne. Tages højde for den trend, der er årstidsbetinget, forårsager gravningen sænkninger i søen af størrelsen 0,03-0,08 m. Der er en god indikation af, specielt i graveperiode 2, at sænkningen optræder momentant, og at den er konstant i tiden.
Der er udført prøvepumpning i grusgraven til bestemmelse af hydrauliske parametre, og der er foretaget opgørelser over opgravede grusmængder. Til kontrol af de udledte formler anvendes data fra graveperiode 1, som havde en varighed på 32 dage. Den gennemsnitligt opgravede mængde anvendes ved gravning 24 timer pr. døgn. Landberg (1992) angiver således følgende data:
| = 27 m., | = 0,18, | = 0,0007 m/s, | = 5440 m3 på 32 dage, |
| = 0,019 m2/s, | = 0,106 m2/s. |
| Af (4.6) fås |
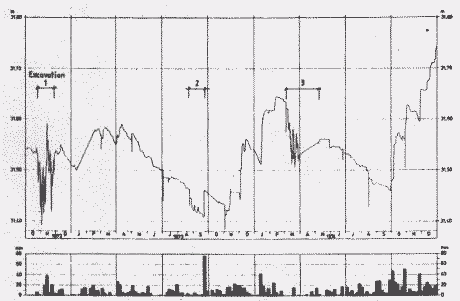
Figur 4.3.
Grundvandsspejl og nedbør ved Örsjö 1972 –10- 01 – 1974-12-31,
(Landberg,1982).
| Da | kan de tilnærmede udtryk anvendes. Af | (4.15) |
| fås |
| og vandspejlssænkningen i søen bestemmes af approksimationen | (4.17) |
| m., hvilket ligger i det | |
| observerede interval. |
I Bilag A er foretaget en gennemregning af formeludtrykkene i et tænkt tilfælde og
sammenlignet med de sænkninger, der forekommer ved pumpning. Det viser sig ikke
overraskende, at sænkningen i grundvandsmagasinet er større, når gravningen opfattes
som pumpning af grundvand. I bilaget er vist, at for små værdier af ![]() kan sænkningerne i grundvandsmagasinet ved gravning
bestemmes ved at beregne sænkningen som ved pumpning fra en boring og dernæst
multiplicere resultatet med
kan sænkningerne i grundvandsmagasinet ved gravning
bestemmes ved at beregne sænkningen som ved pumpning fra en boring og dernæst
multiplicere resultatet med ![]() For små porøsiteter
giver gravning af en volumenenhed grundvandsmagasin, (hvor vandet løber tilbage i graven)
og pumpning af en volumenenhed grundvand altså næsten samme resultat, mens store
porøsiteter giver markant større sænkning ved pumpning. I praksis vil sænkningen ved
gravning som regel altid være små, hvilket hænger sammen med den måde, der graves på,
se afsnit 4.4.
For små porøsiteter
giver gravning af en volumenenhed grundvandsmagasin, (hvor vandet løber tilbage i graven)
og pumpning af en volumenenhed grundvand altså næsten samme resultat, mens store
porøsiteter giver markant større sænkning ved pumpning. I praksis vil sænkningen ved
gravning som regel altid være små, hvilket hænger sammen med den måde, der graves på,
se afsnit 4.4.
4.3 Vådgravningens påvirkning af vandbalancen
Når overjorden fjernes og grundvandet blotlægges som en sø, sker der en ændring af grundvandsbalancen omkring råstofgraven. Opstrøms vil grundvandet normalt strømme ind i graven, mens der nedstrøms kan opstå en kildeskråning, især efter gravningens ophør eller under ophold i graveaktiviteterne. Under gravning kan der dog være tilstrømning til graven langs alle sider, afhængig af gravehastigheden. Men det er vigtigt at notere, at der ikke fjernes vand; det flyttes fra et nærområde omkring graven ind i selve graven, hvorfra det løber tilbage til grundvandszonen.
Under nedbørshændelser infiltreres søen direkte og vil derfor modtage mere vand end det omgivende grundvandsmagasin, og vand vil strømme ud af graven. Når nedbøren når grundvandsspejlet, vil grundvandet stige højere end inde i søen på grund af porøsiteten i grundvandsmagasinet, og grundvand løber tilbage til søen. Til gengæld mister søen vand på grund af fordampning. Denne fordampning afhænger af atmosfæriske forhold som vind, temperatur, luftfugtighed m.v., samt vandspejlsdybden i forhold til det omgivende terræn.
Landberg (1982) gennemgår eksempler på fordampning fra grusgravssøer i det nordlige Tyskland og i Sverige under klimatiske forhold, der er sammenlignelige med de danske. Det generelle indtryk er, at den årlige fordampning er 10-15% mindre end nedbøren. Den nettoinfiltration, som søen unddrages fordi dæklagene mangler, skal holdes op imod denne vandmængde, således at vådgravning ikke kan siges at udgøre en væsentlig belastning af grundvandsressourcerne. Som nævnt i indledningen er dette en opfattelse, som deles af hydrogeologer i amterne og af entreprenører, som driver råstofgrave, hvor der indvindes materiale ved gravning under grundvandsspejlet, uden at der iøvrigt foregår nogen grundvandsoppumpning. Diskussionen omkring en råstofsøs vandbalance er gennemgået mere detaljeret i Miljøministeriet (1992), hvortil henvises.
4.4 Diskussion af resultater
De opstillede formler for sænkningen i en råstofgrav og grundvandsmagasinet omkring graven er relativt simple, og elementerne i dem er velkendte fra prøvepumpning af boringer. Formlerne er udledt under de sædvanlige forudsætninger om homogenitet og isotropi, konstant gravehastighed, grundvandsmagasin af uendelig udstrækning o.s.v. Det er endvidere en forudsætning, at gravningen foregår til bunds af grundvandsmagasinet, således at det er hele grundvandsmagasinet, der fjernes. Gravningen foregår således, at graven udvider sig radiært og radius i graven vokser med kvadratroden af tiden.
Disse forudsætninger er naturligvis aldrig opfyldte på et konkret sted, men ligesom det er tilfældet ved tolkning af data fra prøvepumpninger, må det formodes at formeludtrykkene er en så tilpas tilnærmelse til virkeligheden, at de giver et virkelighedsnært billede af følgevirkningerne af en vådgravning, som det blev demonstreret ved eksemplet fra Örsjö ovenfor.
Formlerne forudsætter, at gravningen starter til tiden t=0 og fortsætter til aktiviteten endeligt ophører. Dette vil naturligvis medføre sænkninger som vokser med tiden i grundvandsmagasinet, mens sænkningen i graven er tidsuafhængig og således udgør den maksimale sænkning der kan opnås. Dette gør det muligt umiddelbart at anvende formlerne til at beregne sænkninger i forskellige afstande til forskellige tider. I praksis vil der altid være pauser i gravningen således, at vandspejlet får mulighed for at retablere sig. Når gravningen så starter igen, er der i graven opsamlet en buffer af vand, som dæmper sænkningernes størrelse. Jo større fri vandoverflade, jo større er denne buffer. Derfor vil det være en sund praksis at etablere en så stor sø som praktisk muligt i starten af gravningen for derved at mindske sænkningerne. Denne buffereffekt er en væsentlig årsag til, at der ikke observeres sænkninger i og omkring råstofgrave, hvor der vådgraves.
Før formlerne kan anvendes, skal der udføres en prøvepumpning til bestemmelse af hydraulisk ledningsevne og porøsitet. Dette foregår efter helt velkendte principper. Det anbefales, at der opstilles et pejleprogram omfattende råstofsø og boringer i nærheden af graven til dokumentation både af forudsigelser og de aktuelle følgevirkninger. Endvidere bør der holdes regnskab med det opgravede volumen på daglig eller ugentlig basis og opsættes regnmåler til daglig opgørelse af nedbøren.
4.5 Oversigt over formler og fremgangsmåde
Ved beregning af sænkningen i råstofgraven benyttes følgende fremgangsmåde:
| Ud fra de givne størrelser | , | og |
| bestemmes først diffusiviteten | eller |
| Her er | grundvandsmagasinets vandmættede tykkelse, |
| er porøsiteten, | er det opgravede volumen råstof over perioden |
| , og | er den hydrauliske ledningsevne. |
Dernæst bestemmes af (4.6)
| , og af (4.15): |
| Her betegner | det såkaldte eksponentielle integral, der også er |
| kendt som boringsfunktionen | .I praksis kan benyttes |
| tilnærmelsen | (4.19): |
| – |
| For | er de to første led en tilstrækkelig approksimation. |
| Sænkningen | i råstofgraven bestemmes af | (4.16): |
| , hvor |
| er bestemt ovenfor. Denne værdi af sænkningen i søen vil altid være |
| worst case. I de fleste praktisk forekommende tilfælde vil en tilnærmelse til |
| svarende til approximationen ovenfor være tilstrækkelig | (4.17): |
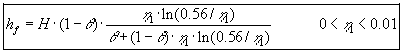 |
| Sænkningen i grundvandsmagasinet | bestemmes af | (4.18): |
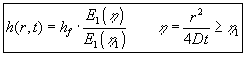 |
| er bestemt allerede og | ||
| kan atter bestemmes ved hjælp af approksimationen ovenfor. |
||
Det ses af formlerne, at sænkningen i graven er tidsuafhængig, altså en konstant, som afhænger af gravekapacitet og fysiske parametre, mens sænkningen uden for graven er tidsafhængig. Figur 4.4 viser en skitse af dette.
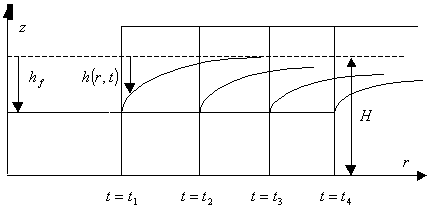
Figur 4.4
Skitse af sænkninger under vådgravningsprocessen
|
|