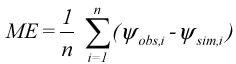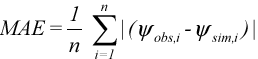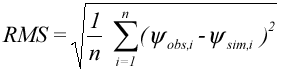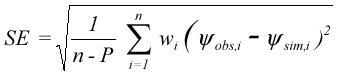|
Retningslinier for opstilling af grundvandsmodeller Appendix A: Kvantitative kalibreringskriterierKvantitative kalibreringskriterier (Sonnenborg, 2000a) baseres hyppigt på et mål for den gennemsnitlige afvigelse mellem observeret og simuleret værdi, også benævnt en norm. Nedenfor er angivet fire normer, som vægter de enkelte residualer på forskellig måde. ME (mean error eller middelfejl) udtrykker den gennemsnitlige afvigelse mellem observeret y obs og simuleret y sim tilstandsvariabel hvor n er antallet af observationer. ME kan give et indtryk af, om der introduceres nogen overordnet fejl i modelresultaterne, dvs. om f.eks. trykniveauet simuleres generelt for lavt eller højt. Hvis ME ® 0, vil der globalt set ikke optræde systematiske fejl i modellen.
MAE (mean absolute error eller gennemsnitlig absolut fejl) beregner et gennemsnit af de absolutte residualer
RMS (root mean squared error eller middelværdien af kvadratafvigelses-summen) er det kriterium, der oftest anvendes til at måle den opnåede overensstemmelse mellem data og model. Denne norm beregner standardafvigelsen på residualerne, og kan sammenlignes direkte med den estimerede standardafvigelse på observationsdata. SE (standard error, goodness of fit eller standardafvigelsen) er et direkte mål for modellens evne til at reproducere de observerede data
hvor wi er vægtningen af observationsdata nr. i, og P
er antallet af kalibreringsparametre. I en regressionsmæssig sammenhæng angiver n
– P antallet af frihedsgrader. Hvis vægtene wi specificeres
til den reciprokke værdi af variansen på observationerne (wi = 1/si2),
vil denne norm tage hensyn til, at der kan være forskellig usikkerhed knyttet til
observationsværdierne. Når samtlige modelfejl er elimineret og kun observationsfejl
resterer, vil SE ® 1. SE giver dermed et direkte
mål for, hvor godt de observerede værdier simuleres i forhold til usikkerheden på
observationerne. 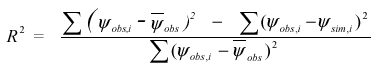
hvor y obs er middelværdien af de observerede data. R2 udtrykker, hvor stor en del af den totale variation i observationsdata, som bliver forklaret af modellen. R2 er med andre ord et mål for tilpasningsgraden af den optimerede model. R2 kan maksimalt blive 1.0, hvilket er udtryk for en perfekt overensstemmelse mellem observeret og simuleret tilstandsvariabel, og er ubegrænset nedadtil. Hvis R2 bliver mindre end 0.0, giver middelværdien af de observerede data en bedre beskrivelse af data end modellen gør, og der er i dette tilfælde grund til at reformulere modellen. R2 anvendes ofte til kvantificering af overensstemmelsen mellem tidsserier af observeret og simuleret tilstandsvariabel. |