|
Kort, nivellering og arbejdsmiljø 1. Kortteknik og nivellering
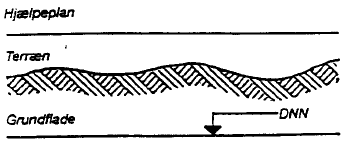
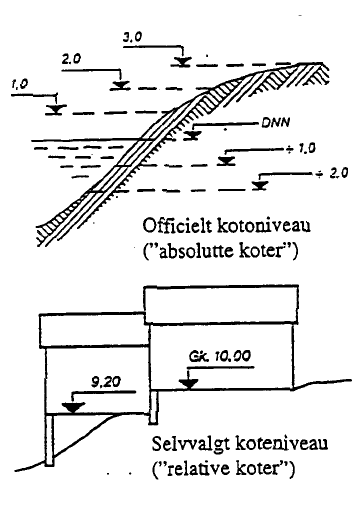
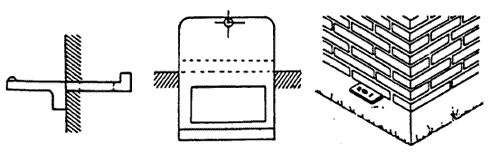
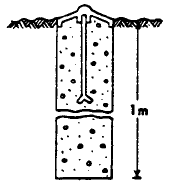
Landmåling består af opmåling, herunder nivellering. Resultaterne opnås gennem måling, beregning og grafisk fremstilling (korttegning). Afsætning kan populært beskrives som den modsatte opgave af opmåling. Afsætning vil typisk bestå i afsætning af punkter, linier og kurver ud fra allerede kendte punkter (fikspunkter). Ved opmåling og afsætning arbejder man i forhold til en vandret grundflade. Denne grundflade, der ligger i højde med middelvandstanden omkring Danmark, kaldes "Dansk normal nul" (D.N.N.), i det følgende også benævnt: absolutte koter. Indføres en hjælpeplan (jf. Figur 1)vil det svare til, at der arbejdes forskudt i forhold til D.N.N. Sådanne koter benævnes i det følgende som relative koter. Jordens krumning har betydning ved store opmålinger over store afstande. Ved afstande op til 7 km kan der ses bort fra jordens krumning. 1.1 KoordinatsystemerKoordinatsystemet og landskoordinatsystemet For at kunne opmåle og afsætte i vandret plan, er det nødvendigt at arbejde med koordinater. Koordinatsystemet indenfor landmåling også kaldet "Landskoordinatsystemet" eller system 34 er placeret således, at hele landet ekskl. Bornholm har positive koordinater. Systemet er orienteret nord/øst-vest således, at Agri Baunehøj på Djursland har koordinaterne (200,000;200,000) med enheden km. Oplysninger om koordinater og landskoordinatsystemet i øvrigt fås hos Kort- og matrikelstyrelsen. 1.2 KoterKoter, herunder relativ/ absolutte koter og hovedfikspunkter Terrænpunkters højdeforhold (niveau) angives ved hjælp af koter. Koterne fastsættes i forhold til allerede kendte punkter, også benævnt fikspunkter. Der kan arbejdes ud fra to typer fikspunkter (koteniveauer). 1. Et officielt koteniveau. Til tider også benævnt ìabsolutte koter". Det officielle koteniveau er fastlagt af Kort- og Matrikelstyrelsen (tidligere Geodætisk Institut (GI)) ved at foretage vandstandsmålinger i en række danske havne. Middelvandstanden for denne landsdækkende nulplan kaldes som tidligere angivet "Dansk Normal Nul" eller i daglig tale D.N.N. (Se Figur 2) Ud over landet findes en lang række fikspunkter angivet D.N.N. med hovedfikspunkt på Århus Domkirke med koten 5,615 m. Fikspunkterne er placeret dels på bygningsfundamenter (Se Figur 3), dels på betonstøbninger i terrænet. Meget benyttet ved fundamenter er en støbejernsplade, der rager 40-50 mm frem og bærer en lille kuglekalot, hvis overside angiver fikspunktets nøjagtige beliggenhed. I terrænet kan fikspunktet være en støbejernskalot, faststøbt i en jernbetoncylinder, som er nedgravet i jorden således, at den kun rager ganske lidt op over terrænet (Se Figur 4). Fikspunkter er fredede og må ikke fjernes.
Figur 1
Figur 2
Figur 3
Figur 4
Figur 5
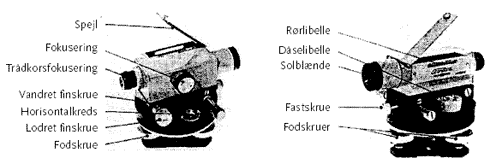
Figur 6 Oplysninger om disse fikspunkters placering, opbygning og kote kan indhentes ved de lokale byggemyndigheder (Teknisk forvaltning, Bygningsinspektoratet eller Kort- og Matrikelstyrelsen). Oplysningerne gives i form af en kort beskrivelse af punktets placering på bygningen samt et kortbilag. GI punkterne kontrolleres løbende af Kort- og Matrikelstyrelsen, da punkterne kan beskadiges eller "sætte sig" med tiden. Derfor bør man ikke bruge gamle "kendte" koter, men hos lokale myndigheder eller Kort- og Matrikelstyrelsen, få oplyst korrekt kote på det valgte udgangspunkt. 1.3 MåleudstyrMåleudstyr generelt Stadiet er en 3-4 m lang målestok, inddelt i cm, dm og m med Hvid/rød og hvid/ sort bemaling. For tydeligt at kunne skelne 1 meter fra 2 meter osv. er stadiet ofte udført med farveskrift (rød-sort) og særlig mærkning for hver meter (se Figur 5). Under opmålingen er det nødvendigt at skønne millimeteraflæsningen, hvis denne nøjagtighed er påkrævet, da det kun er meter, tiendedele- og hundrededele meter (m, dm, og cm), der kan aflæses direkte.
Figur 7
Figur 8
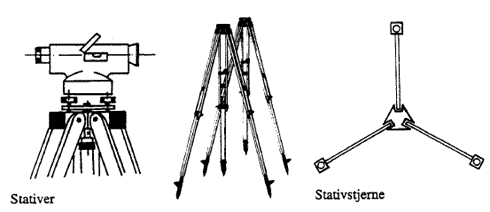
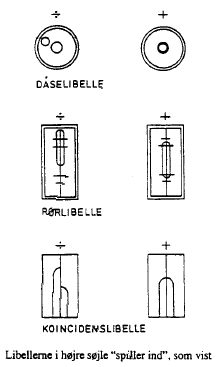
Under brugen (måling) skal stadiet holdes lodret, hvilket kan sikres ved brug af en dåselibelle. Denne kan enten være indbygget i stadiet eller være i løs udgave, der holdes mod stadiets kant. Det er vigtigt for målenøjagtigheden, at stadieholderen hele tiden er opmærksom på at holde stadiet lodret. Dette kan være vanskeligt i stærk blæst. 1.3.2 StativetStativ og stativstjerne Stativet er fremstillet i træ eller metal, og består af en topplade og sammenskydelige ben. Ved opstilling af stativet skal benene trædes fast i jorden og toppladen placeres omtrent vandret i arbejdshøjde ved hjælp af de forskydelige ben. På befæstede arealer (asfalt, beton, fliser), kan det være nødvendigt at bruge en "stativstjerne", der udlæges på jorden, så stativet ikke flytter sig under målingerne (se Figur 6). I forbindelse med flytning løftes stativet med instrumentet påmonteret og bæres på skulderen til næste målested. 1.3.3 InstrumenterInstrumenter, herunder retvendt/omvendte og forskellige typer Der findes mange forskellige typer instrumenter, fx
Ud over ovenstående opdeling kan instrumenterne opdeles i følgende hovedtyper:
Førstnævnte hovedtype - "omvendt instrument" - omtales ikke i det følgende, da deres udbredelse er meget aftagende. Ved brug af instrumenter er det vigtigt:
|
| enten med 3 fodskruer | |
| eller med kuglehoved (håndgreb under instrument). |
For begge typer gælder følgende opstillingsprocedure:
| placer instrumentet på stativhovedet | |
| indstil efter dåselibelle ved hjælp af enten fodskruer eller flytning på kuglehoved. (Se Figur 10) |
Derpå er instrumentet klar til brug, idet den indbyggede automatik sikrer et vandret sigte.
1.4 Udførelse af nivellering
Nivellering er fastlæggelse af højdeforskellen mellem to eller flere punkter. Koten til det første punkt (fikspunkt) skal være kendt.
Nivellering udføres som følger (Se Figur 11):
| instrument opstilles ca. midt mellem to punkter | |
| stadiet placeres på punkterne (først fikspunkt) | |
| kikkertakse og dermed sigteplan stilles vandret (opstilling af instrument) | |
| trådkors stilles skarpt (kun ved start) | |
| drejning ved hjælp af fastspændingsskruen (spænd med måde) | |
| sigt efter stadiet ved hjælp af sigtekorn | |
| fokuser kikkerten og finjuster, så stadiet er i midten | |
| kontroller libelle med finskrue | |
| aflæsning på stadie foretages (midterste tråd) | |
| resultaterne indskrives i målebog. |
Der afsluttes med kontrol af libelle og aflæsning. Udregning af koter kan evt. udføres senere, når opmålingen er afsluttet.
Princippet i nivellering (opstilling og aflæsning) er vist på tegningen.
1.4.1 Koteberegning
Formler for koteberegning
Koteberegningen sker med udgangspunkt i den angivne kote (fikskote).
- Bestemmelse af sigteplanskote:
Sigteplanskote = kendt kote (fikskote) + aflæsning. - Bestemmelse af koter:
Kote = sigteplanskote - aflæsning.
Vigtigt
Inden hver aflæsning skal der ikke stilles på fodskruer eller håndgreb. Nogle instrumenter har et indbygget advarselslys, der kommer frem, hvis instrumentet ikke kan sikre vandret sigteplan.
1.4.2 Føring og udregning af målebogsblade
Efterhånden som der foretages aflæsninger under udførelse af et nivellement, føres disse i en målebog eller på et løst målebogsblad.
I forbindelse med føring af målebog er følgende forhold vigtige at bemærke:
| korrekt udfyldning af målebogsbladets hoved | |
| korrekt udfyldning af kolonner for opstilling, punktnummer og aflæsning | |
| tydelig udfyldning således, at en fagkyndig (3. person) uden hjælp kan læse og evt. færdigudregne målebogen. |
Efter endt opmåling og resultaterne indført på målebogsbladet, kan det se ud som i skemaet.
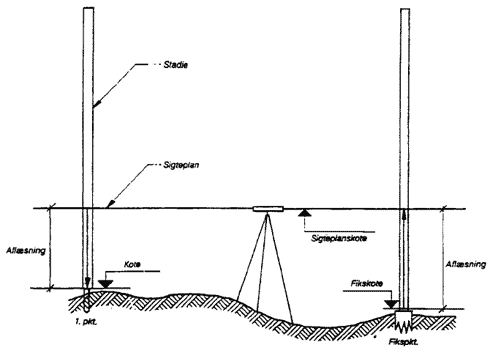
Figur 11
Princippet i nivellering
1.4.3 Målebogsblad (Se Figur 12)
Eksempel på beregnet målebogsblad
sagsnr. |
Byggevej 15 |
|
init. |
ab, kh |
side 1 |
opstilling |
punkt |
aflæsning |
sigteplan |
kote |
anmærkning |
1 |
0 |
2,22 |
7,22 |
5,00 |
fikspunkt |
|
1 |
1,37 |
|
5,85 |
|
1.4.4 Eksempel på koteberegning
| Fikskote | (pkt. 0) = 5,00 |
| Aflæsning | (pkt. 0) = 2,22 |
| Aflæsning | (pkt. 1) = 1,37 |
| Løsning | |
| Sigteplanskote | = Fikskote + aflæsning |
| = 5,00 + 2,22 | |
| = 7,22 | |
| Kote (pkt. 1) | = Sigteplanskote - aflæsning |
| = 7,22 - 1,37 | |
| = 5,85 |
1.4.5 Linienivellement
Udførelse af linienivellement
Ved et linienivellement fastlægges højdeforholdene langs en linie. Derved fremskaffes det nødvendige grundlag fx i forbindelse med planlægningen og udførelse af et stykke arbejde.
Linienivellementet kan udføres enten som enkeltlinienivellement (uden kontrol) eller som dobbelnivellement (med kontrol) af en stationeret linie pr. 20, 25 eller 50 m.
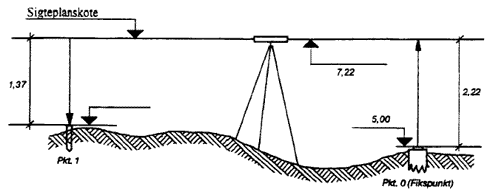
Figur 12
Data til målebordsblad
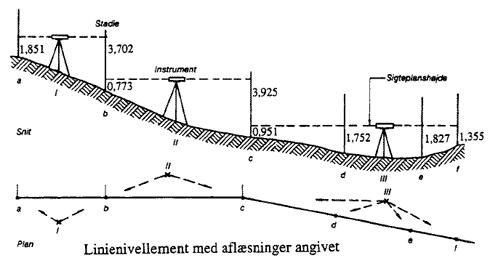
Figur 13
Linienivellement
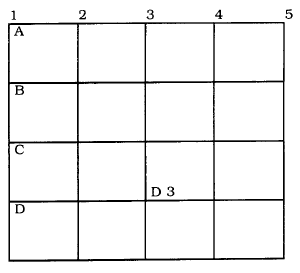
Figur 14
Kvadratnet
Det er vigtigt at planlægge arbejdet således, at flest mulige punkter kan indmåles i hver opstilling. Følgende skal iagttages:
- max 80 m sigte
- forhindringer i linien
- i bakket terræn opstilles i 3. dels punkter
- min. 2 m's afstand til stadie.
Linien skal være udmålt og afmærket eller afpælet, inden nivellementet kan udføres. Linien kan bestå af både retlinede strækninger og af kurver.
I Figur 13 vises principperne i udførelse af et linienivellement. Der er tale om tre opstillinger (I, II, III) med start af målingerne fra pkt. a (fikspunkt).
1.4.6 Målebogsblad
Føring af målebogsblad ved linienivellement
sagsnr. |
Byggevej 25 |
dato |
init. |
ab, kh |
side 2 |
opstilling |
punkt |
aflæsning |
sigteplan |
kote |
anmærkning |
1 |
a |
1,851 |
14,351 |
12,500 |
fikspunkt |
|
b |
3,702 |
|
10,649 |
|
|
b |
0,773 |
11,422 |
10,649 |
overgangsp. |
|
c |
3,925 |
|
7,497 |
|
|
c |
0,951 |
8,448 |
7,497 |
overgangsp. |
|
d |
1,752 |
|
6,696 |
|
|
e |
1,827 |
|
6,621 |
|
|
f |
1,355 |
|
7,093 |
|
Der anvendes følgende betegnelser for punkterne:
| a kaldes startpunkt (fikspunkt) | |
| b og c kaldes overgangspunkter | |
| d og e kaldes mellempunkter | |
| f kaldes slutpunkt |
Det skal bemærkes, at en fejl i:
| et overgangspunkt vil give anledning til fejl, der vil føres med videre frem i nivellementet, da koten føres videre frem | |
| et mellempunkt kun vil give anledning til en lokal fejl, da koten ikke føres videre. |
1.5 Fladenivellement
Fladenivellement og fastlæggelse af højdekurver
Skal man på en tegning angive højdeforholdene for et areal, kan dette ske ved at foretage et fladenivellement.
Det er karakteristisk for en højdekurve (niveaukurve), at alle punkter har samme kote (niveau). Lidt populært kan det anskues således: Hvis man "gik en tur" langs en højdekurve, ville man hele tiden befinde sig i samme højde (niveau).
Det er valgt her at gennemgå fladenivellementet efter kvadratnetmetoden, men der findes andre metoder, hvis anvendelighed er afhængig af terrænets beskaffenhed. Ved kvadratnetmetoden lægges et kvadratnet ud over terrænet som vist på Figur 14.
1.5.1 Kvadratnet
Fastlæggelse af punkter i et kvadratnet
Sidelinien i kvadratet vælges efter opgavens omfang og terrænets beskaffenhed fra 5 til 25 m.
For at holde styr på punkterne gives disse numre, oftest bestående af et dobbeltnummer (både tal og bogstav, fx D3, se figur 14) hidrørende fra de krydsende linier.
Udførelse
Kvadratnettet afsættes i marken ved hjælp af stålbåndmål, vinkelprisme og stokke. Diagonalerne i nettet kontrolleres.
I nettets skæringspunkter nedbankes pæle i plan med terrænet eller pæle mærket fx ved 200 mm og nedbankes til dette mærke.
Disse pæle nivelleres, og koterne i krydspunkterne bestemmes.
Det er vigtigt at huske følgende:
| nivellementet afsluttes med, som kontrol, at nivellere fikspunktet | |
| kvadratnettet nedtages ikke (fjernes ikke) før koterne er beregnet, indskrevet på tegningen og niveaukurverne konstrueret. Skulle der under færdiggørelsesarbejdet vise sig fejl og mangler, kan der foretages kontrol- eller ekstramålinger i marken. |
1.5.2 Beregning af niveaukurver
Eksempler på beregning af niveaukurver
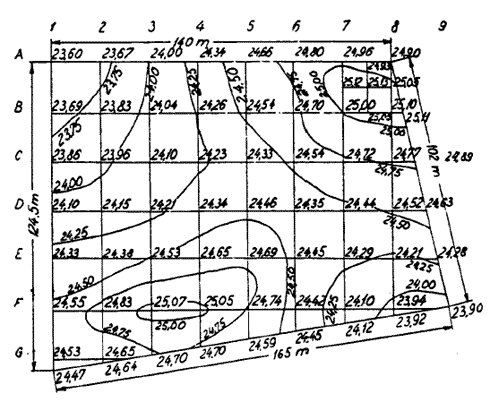
Konstruktionen af kurverne kræver en beregning. I Figur 15 vises et eksempel på et fladenivellement. Figuren viser et areal med de beregnede niveaukurver indtegnet.
For at finde kurvernes skæringspunkter med kvadratnettet regnes der med retlinet (ens) flade mellem to nabopunkter. Højdeforskellen mellem kurverne fastsættes til 0,25 m.
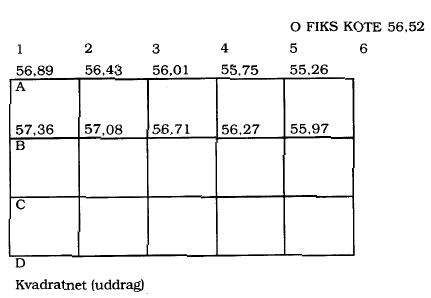
I Figur 16 vises en skitse af et fladenivellement (i uddrag). Det tilhørende målebogsblad:
sagsnr. |
sagsnr. |
Kh-2 |
init. |
Ab-kh |
Side 1 |
opstilling |
punkt |
aflæsning |
sigteplan |
kote |
anmærkning |
1 |
fiks |
1,49 |
58,01 |
56,52 |
fiks punkt |
|
A 1 |
1,12 |
|
56,89 |
|
|
A 2 |
1,58 |
|
56,43 |
|
|
A 3 |
2,00 |
|
56,01 |
|
|
A 4 |
2,26 |
|
56,75 |
|
|
A 5 |
2,75 |
|
55,26 |
|
|
B 1 |
0,65 |
|
57,36 |
|
|
B 2 |
0,93 |
|
57,08 |
|
2 |
B 2 |
1,20 |
58,28 |
57,08 |
overgangsp. |
|
B 3 |
1,57 |
|
56,71 |
|
|
B 4 |
2,01 |
|
56,27 |
|
|
B 5 |
2,31 |
|
55,97 |
|
Fladenivellement (uddrag)
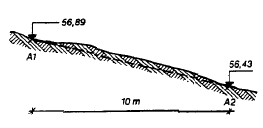
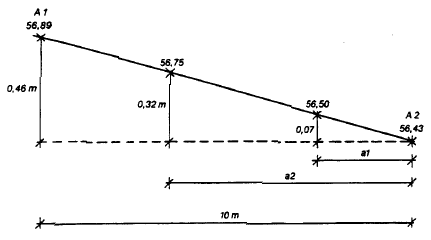
I Figur 17 betragtes terrænet mellem punkterne A 2, A 1.
Kote 56,50 og 56,75 ligger et sted mellem A 2 og A 1.
Dette betyder, at beliggenheden af kurven (skæringspunktet) for både kote 56,50 og kote 56,75 skal findes.
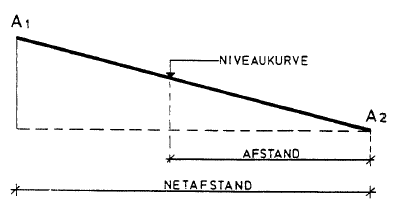
Ved at anvende en geometrisk sætning om ens vinklede trekanter, kan der opstilles følgende formel
![]()
Se Figur 18.
Figur 15
Eksempel på fladenivellement
Figur 16
Skitse
Figur 17
Figur 18
Figur 19

Figur 20
Teodolit
Eksempel
Vi ønsker at bestemme de skæringer, der er mellem netpunkt A 1 og A 2. (se målebogsblad og Figur 19).
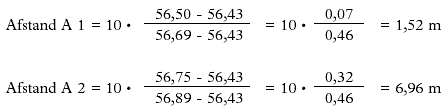
De fundne afstande kan nu afsættes fra punktet A 2. Ganske samme fremgangsmåde benyttes mellem resten af kvadratnettets punkter
Når ovennævnte er beregnet for hele nettet og afsat på en tegning, kan kurverne med den indbyrdes højdeforskel på 0,25 m tegnes.
1.6 Teodolitten
Teodolitten betegnes også som et vinkelmåleinstrument, da det i modsætning til et nivelleringsinstrument kan bruges til både vandrette og lodrette planer. Teodolitten anvendes til såvel opmålings- som afsætningsopgaver.
Under målingen er teodolitten fastspændt på et stativ (treben), placeret nøjagtig lodret over fikspunkt eller målepunkt. Denne placering sikres ved hjælp af snorlod, stanglod eller optisk lod.
Største måleafstand for mm aflæsning er ca. 60 m. Største måleafstand for cm aflæsning ca. 180 m.
1.6.1 Brug af teodolit
Brug af forskellige typer teodolitter
Indstilling af trådkors og billede (Se Figur 20):
For at kunne måle omhyggeligt er det vigtigt, at trådkors er indstillet skarpt. Dette gøres ved at dreje okularet (3), mens man retter kikkerten mod himlen. Dernæst rettes kikkerten mod et fjernt mål, og kikkertbilledet stilles skarpt med focuserknappen (2).
Indstilling på signal (stok, genstand mv.)
Med løsnede låseknapper (1 og 10) drejer man kikkerten, så sigtekornet på denne (7) står på signalet. Derefter spændes låseknapperne, og nu kan teodolitten kun drejes ved hjælp af finskruerne.
Nu stiller man kikkertbilledet skarpt med focuserknappen. Ved hjælp af henholdsvis vertikalfinskruen (8) og horisontalfinskruen (9) indstilles trådkorset nøjagtigt på signalet.
1.6.2 Kredsaflæsning
Kredsaflæsning på teodolitten
Kredsens belysning sker med en optik, der får lyset koncentreret via et udvendigt spejl, der kan drejes. Ved dårlig belysning kan nogle instrumenter monteres en elektrisk lyskilde.
Kredsen stilles skarpt, og aflæsning foretages. Skalaens opbygning/indretning kan variere fra det ene instrument til det andet, hvorfor der henvises til instruktionsbogen. Instrumenter med digital display kan aflæses direkte. (Se Figur 21).
Vigtigt
Aflæs på korrekt skala:
H eller AZ for vinkler i vandret plan.
V for vinkler i lodret plan.
Bemærk om der arbejdes med 360° eller 400g
Se Figur 22.
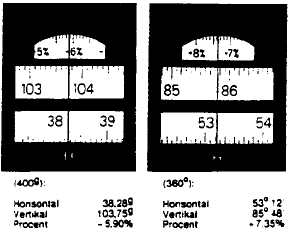
Figur 21
Digital display
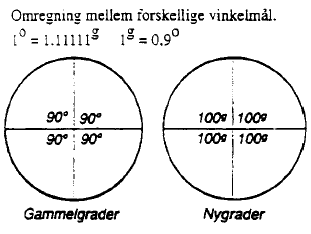
Figur 22
Gammelgrader og nygrader
1.6.3 Gradmåling
En cirkel er opdelt i grader. Graderne angiver vinklens størrelse, både i vandret og lodret plan.
Man regner med 2 slags grader - gammelgrader og nygrader.
Gammelgrader
Cirklens omkreds = 360°
En ret vinkel = 90°
1° = 60` min
1` = 60"sek
Nygrader (gon)
Cirklens omkreds = 400,00g
En ret vinkel = 100,0g
Ved nygrader regnes der med decimaler (10 talssystemet). Nygrader anvendes i dag mere og mere ved opmålings- og afsætningsopgaver og vil nok, om få år, helt afløse "gammelgrade" systemet.
1.6.4 Måling af vinkler
| indstil kikkerten på 1. stok | |
| aflæs skalaen | |
| drej kikkerten og indstil på 2. stok | |
| aflæs skalaen. |
Ønskes større nøjagtighed slås kikkerten igennem, målingen gentages, og gennemsnittet beregnes.
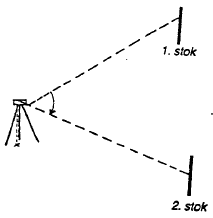
Figur 23
Måling af vinkel
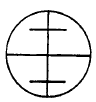
Figur 24
Afstandsstreger
Eksempel, beregning af vinkel
|
Gammelgrader |
Gammelgrader |
Nygrader |
1. aflæsning |
0,000° |
0° 0`0" |
0,000g |
- 1. aflæsning |
60,000° |
60° 0`0" |
66,667g |
= vinkel på |
60,000° |
60° 0`0" |
66,667g |
Afsætning af vinkel
| indstil kikkerten på 1. stok | |
| nulstil kredsen (00 0`0") | |
| drej kikkerten det ønskede antal grader | |
| fastskru instrumentet og afsæt 2. stok i sigtelinien | |
| kontroller på skalaen. |
Eksempel
|
Gammelgrader |
Gammelgrader |
Nygrader |
1. aflæsning |
0,000° |
00°`0" |
0,000g |
- 2. aflæsning |
60, 000° |
60° 0`0" |
66,667g |
= vinkel på |
60,000° |
60° 0`0" |
66,667g |
1.6.5 Optisk afstandsmåling
Både med nivelleringsinstrument og teodolitter er det muligt at foretage optisk afstandsmåling, hvis instrumentets trådkors er forsynet med to såkaldte afstandsstreger (figur 24).
Disse 2 yderste streger bruges til måling af afstanden fra instrumentet til stadiet, idet stadiet aflæses på sædvanlig vis. Afstanden fremkommer ved at gange forskellen mellem aflæsningerne med 100.
Eksempel:
| aflæsning øverste streg | 1,285 |
| aflæsning nederste streg | 0,844 |
| forskel | 0,441 |
Afstanden mellem stadie og instrument er da lig med 100 x 0,441 = 44,1 m.
Afstandsmålingen kan endvidere foretages ved elektronisk distancemåling. Det kan enten være indbygget i instrumentet eller være en selvstændig enhed, der påmonteres.
1.7 Koordinatsystemet
Koordinatsystemet med de fire kvadrater
Det todimensionelle koordinatsystem består af to tallinjer, der står vinkelret på hinanden og har fælles nulpunkt, som vist på Figur 25.
De to tallinjers skæringspunkt kaldes koordinatsystemets nulpunkt. De to tallinier kaldes koordinatssystemets akser. Den vandrette kaldes abscisseaksen og den lodrette ordinataksen.
De betegnes, når koordinatsystemet anvendes indenfor den rene matematik, i reglen med bogstaverne x og y, og betegnes i så fald ofte som henholdsvis x-aksen og y-aksen.
Man ser, at de to akser deler planet i fire dele, der kaldes første, anden, tredje og fjerde kvadrant, som angivet på Figur 25.
Et koordinatsystem er bestemt ved beliggenheden af dets nulpunkt.
Koordinatsystemet benyttes til at angive et punkts beliggenhed i planet. Det gøres ved at tildele punktet to koordinater. Den første af disse angiver det antal enheder, man skal bevæge sig hen ad abscisseaksen for at komme lodret under eller over punktet.
Denne koordinat kaldes punktets abscisse. Den anden koordinat angiver, hvor mange enheder man skal bevæge sig op eller ned for at komme vandret ud for punktet; den kaldes punktets ordinat.
Et punkts koordinater angives som et talpar. Inden i en parentes skriver man først abscissen, derefter et komma og sidst punktets ordinat, således (abscisse, ordinat).
På Figur 25 er indtegnet fem punkter. De har følgende koordinater:
P1: (3,2); P2: (1,4 2,5); P3: (-2,2); P4 (-4,-3); P5: (3,2).
Vi ser heraf, at koordinaterne kan være både hele tal og decimaler (samt naturligvis brøker eller blandede tal). Ud over dette ser vi:
| punkter i første kvadrant har positiv abscisse og positiv ordinat | |
| punkter i anden kvadrant har negativ abscisse og positiv ordinat | |
| punkter i tredje kvadrant har negativ abscisse og negativ ordinat | |
| punkter i fjerde kvadrant har positiv abscisse og negativ ordinat |
I landskoordinatsystemet udnyttes kun 1. Kvadrant, idet 0-punktet er defineret så den trigonometriske station: Agri Baunehøj på Djursland (et af Geodætisk instituts 1. Orden`s punkter), har fået koordinaterne y=x=200 km. Herved får både Gedser og Christiansø positive koordinater.
Landskoordinaterne angives normalt i meter med 2 decimaler. Sædvanligvis skrives ordinaten først som fx (y,x) = 289 025.62, 235 891.24.
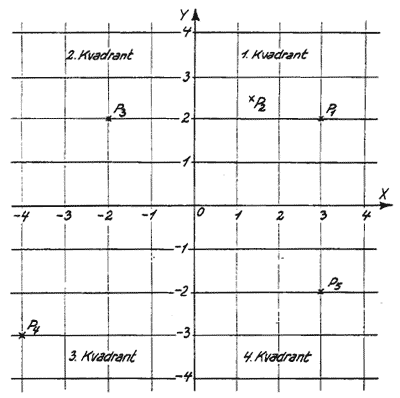
Figur 25
Koordinatsystem
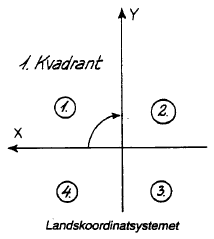
Figur 26
1.8 UTM-nettet
UTM-nettet er opdelt i 60 UTM-zoner, der hver spænder over 6 længdegrader, benævnes zonetal. Således ligger zone 1 mellem 174° og 180° v.l., zone 2 mellem 168° og 174° v.l., etc.; herved kommer Danmark til at ligge i zonerne 32 (6°-12° ø.l.) og 33 (12°-18° ø.l.). (Se Figur 27).
Midtermeridianerne svarende til disse to zoner er altså henholdsvis 9° ø.l. og 15° ø.l., medens meridianen 12° ø.l. danner zonegrænse.
UTM-nettet kan anvendes på to måder (ved angivelser af zonekoordinater eller ved angivelse af kortreferencer).
1.8.1 Zonekoordinater
Anvendelse af UTM-nettet med eksempler
Zonekoordinater refererer direkte til den enkelte zones koordinatsystem, altså til zonens E-akse (ækvator) og dens N-akse. En fuldstændig zonekoordinatangivelse indledes med UTM og efterfølges af:
| zonens nummer | |
| E(asting), med angivelse af enhed | |
| N(orthing), med angivelse af enhed | |
| H(eight) eller H(øjde), ved angivelse af enhed. |
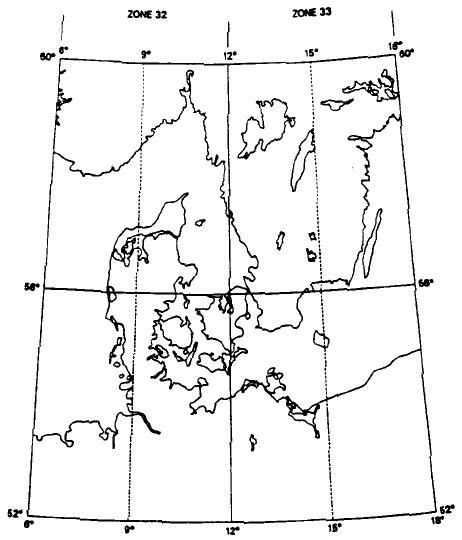
Figur 27
Danmarks placering i zonerne 32 og 33
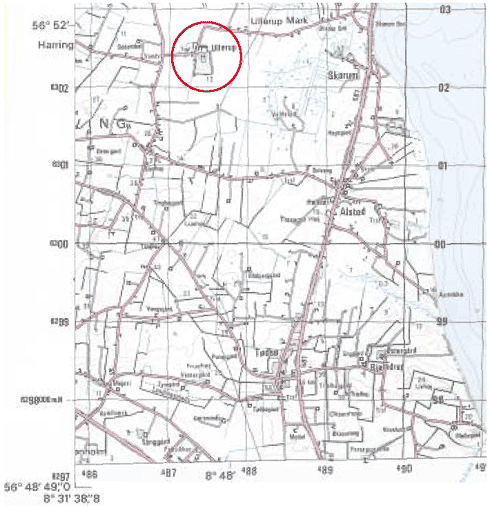
Figur 28
Ullerup
Eksempel
Transformatoren (trsf) umiddelbart vest for gården Ullerup på 4 cm kortet 1116 I SØ Thisted (jf. Figur 28) har koordinaten:
UTM 32 E 487.290 m N 6.302.440 m H 13 m
Tallet 32 fremgår af den i diagrammet Figur 29 viste zonebetegnelse.
E- og N-værdien fremkommer på følgende vis jf. Figur 30 (udmålt på 4 cm kort):
Bestem E- og N-værdi for det nederste venstre hjørne af det 1 km kvadrat i hvilket punktet ligger:
| E = 487.000 m | N = 6.302.000 m |
Bestem ved udmåling i kvadratet og N- værdi for punktet i forhold til kvadratets
nederste, venstre hjørne:
| E = 290 m | N = 440 m |
| Adder | |
| E = 487.290 m | N = 6.302.440 m |
Højden kan (med tilnærmelse) bestemmes ud fra kortets kurvebillede. UTMsystemets
zonekoordinater finder især anvendelse ved beregninger i forbindelse med opmåling
(landmåling) og vil da ofte ses angivet i dm, cm eller mm; fx er koordinaterne for de af
Kort- og Matrikelstyrelsen målte trigonometriske stationer almindeligvis angivet i cm. Er
zonekoordinaterne derimod udtaget fra et kort, bør de ikke angives med flere decimaler
end kortet (dets målestoksforhold, dets topografiske nøjagtighed, nøjagtigheden af
nettets placering) og den metode og omhyggelighed, der anvendes ved udmålingen i kortet,
berettiger til. Almindeligvis bør zonekoordinaterne ikke angives med større
nøjagtighed, end den der svarer til ca. 12 mm i kortets målestoksforhold, dvs. 25 m i 2
cm kortet og 10 m i 4 cm kortet.
1.8.2 Kortreferencer
En kortreference baserer sig på zonens opdeling i bælter af 100 km kvadrater. Den består af:
| zonebetegnelse | |
| bogstavskombination for 100 km kvadratet | |
| E-værdi (uden angivelse af enhed) | |
| N-værdi (uden angivelse af enhed). |
Eksempel:
Gården Ullerup har kortreferencen (Figur 31 - 4 cm kortet 1116 I SØ Thisted) 32 VMJ 874024
Zonebetegnelsen: 32V og bogstavskombinationen for 100 km kvadratet: MJ fremgår af Figur 29.
Talgruppen, der her skal læses som E = 874 hektometer (hm), N = 024 hm, referer til 100 km kvadratetssider (angiver altså afstandene fra punktet til vestlige 100 km linie). De fremkommer på lignende vis, som anført for zonekoordinater (Figur 32).
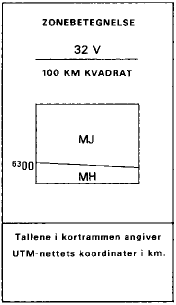
Figur 29
Zonebetegnelse
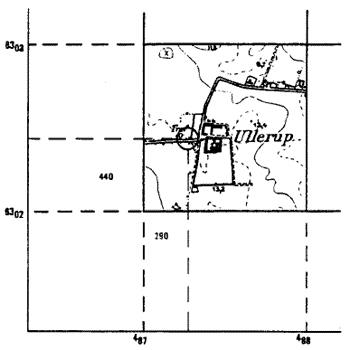
Figur 30
Transformatorstationens koordinater
Bestem E- og N-værdi for det nederste, venstre hjørne af det 1 km kvadrat i hvilket punktet ligger. Anvend kun de store tal, da disse angiver afstande (i km) til 100 km kvadratets sider:
| E = 870 hm | N = 020 hm |
Bestem ved udmåling i 1 km kvadratet E- og N- værdier for punktet i forhold til
kvadratets nederste, venstre hjørne:
| E = 4 hm | N = 4 hm |
| adder | |
| E = 874 hm | N = 024 hm |
Medens zonekoordinater især finder anvendelse ved opmåling, beregning mv., benyttes
kortreferencer udelukkende i forbindelse med kort som et middel til hurtigt og entydig
angivelse af et objekts beliggenhed.
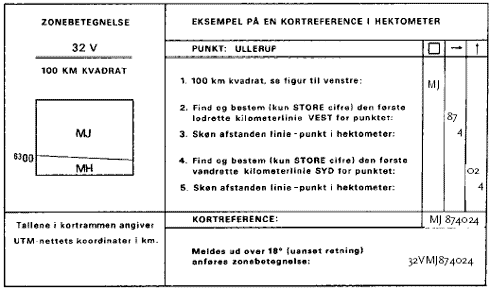
Figur 31
Kortreference
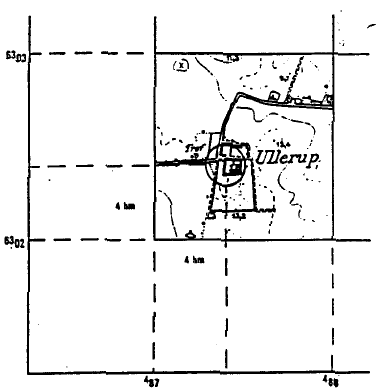
Figur 32
Kortreference for Ullerup
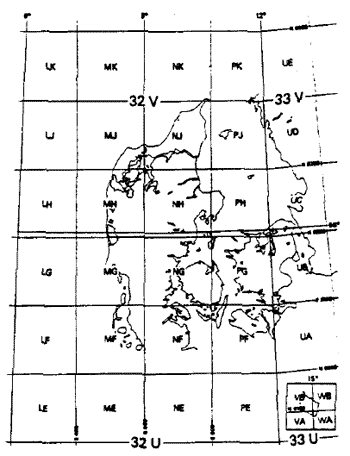
Figur 33
100 km kvadratnet
Der er ingen egentlige regler for hvilke enheder, der skal benyttes, men for 2- og 4-cm kortenes vedkommende vil hektometeren som regel være den mindste og kilometeren ofte tilstrækkelig (i 750 000 kortet henholdsvis km og 10 km). I eksemplet kan man fx anføre:
gård 32VMJ874024
Hvor hektometeren vil være nødvendig for at udskille gården Ullerup fra de øvrige inden for 1 km kvadratet; men man kunne også skrive
Ullerup 32 VMJ8702
og hermed give kortkonferencen i km, der i dette tilfælde er tilstrækkelig, da der ikke findes andre lokaliteter inden for 1 km kvadratet med dette navn.
Det skal understreges, at det er vigtigt, at 0 altid medtages som et ciffer i talgruppen. Det vil altså være forkert at skrive:
32 VMJ87424
Ved korrekt angivelse af talgruppen vil denne altid bestå af et lige antal cifre, og der vil ikke kunne herske tvivl om, at første halvdel angiver Easting-værdien og anden halvdel Northing-værdien. Selv om enheden ikke anføres, kan der heller ikke herske tvivl om denne.
1.9 Litteratur
Nivellering og afsætning (emnehæfte), fællessekretariatet for bygge og anlæg.
Nivellering og afsætning (opgavehæfte), fællessekretariatet for bygge og anlæg.
Teknisk matematik, Erhvervsskolernes forlag.
Teknisk matematik (opgavehæfte), Erhvervsskolernes forlag.
Landmålingspraktik, Erhvervsskolernes forlag.
Nivellement, opmåling og miring, Teknologisk institut.
Geodætiske kort fra Kort og Matrikelstyrelsen, (område 1315).
UTM-NETTET opbygning og anvendelse, Geodætisk institut.
Bilag 1
Borerapport