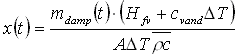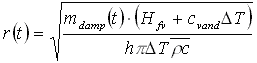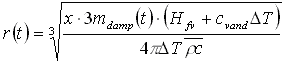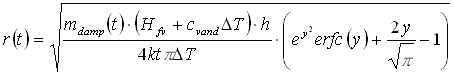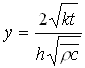| Forside | | Indhold | | Forrige | | Næste |

Modellering af opvarmning ved dampinjektion (Modi)

3. Energibalancemodeller

3.1 Energibalancemodeller uden varmetab

I en energibalancemodel uden varmetab antager man, at al den injicerede energi går til opvarmning af jord til damptemperatur. Der er altså ikke noget energitab fra dampzonen ved varmeledning, strømning af kondensat eller gasfaseekstraktion. Ved hjælp af denne antagelse er det muligt at beregne dampzonens udbredelse som funktion af den injicerede energi, når man samtidig kender den geometri, som dampzonen udbreder sig med.

Energiindholdet for mættet damp kan beregnes ved følgende formel:

hvor m_damp er massen af damp, H_fv er vands fordampningsvarme, c_vand er vands varmekapacitet og D T er temperaturforskellen mellem dampen og jordens temperatur ved dampinjektionens begyndelse.

Energimængden, der kræves for at opvarme jord til damptemperatur, er givet ved følgende formel:

hvor V, r _jord og c_jord er henholdsvis jordens volumen, densitet og varmekapacitet, n er porøsiteten, S_vr er vandmætningen i dampzonen, r _vand er vands densitet og er den overordnede varmekapacitet for et jordvolumen. Energien til opvarmningen af poreluft og eventuel forurening på fri fase er negligeret.

Ved at kombinere disse to formler kan man umiddelbart bestemme, hvor stort et volumen jord, V, en given mængde damp, m_damp, kan opvarme. Når man samtidig kender formen på dette volumen eller dampzonens geometri, har man en model, der kan forudsige dampzonens udbredelse.

I det lineære 1-dimensionale tilfælde får man derved følgende ligning for dampfrontens placering:

hvor x(t) afstanden fra injektionen til dampfronten til tiden t, m_damp(t) er den totalt injicerede mængde damp til tiden t og A er tværsnitsarealet.

Denne formel har været anvendt til analyse af kolonneforsøg med dampinjektion. /5/

I fuldskalaoprensninger vil dampzonen ikke udbrede sig lineært, og man må benytte en anden volumenfunktion. Antager man, at dampzonen udbreder sig radialt som en cylinder kan man få følgende formel:

hvor r(t) er afstanden fra injektionen til dampfronten til tiden t og h er højden af dampzonen. Denne formel har været brugt i /2/ til analyse af en fuldskalaoprensning som er nærmere gennemgået i afsnit 8.1.

Forudsætningen for at anvende formlen er, at dampzonen kun udbredes horisontalt, hvilket kræver, at den horisontale permeabilitet er mange gange større end den vertikale.

Man kunne også forestille sig, at dampzonen ligeledes udbredte sig i vertikal retning og i stedet tilnærme dens form med en ellipsoide, hvor der var en fast sammenhæng mellem udbredelsen i vertikal og horisontal retning. Eksempelvis kunne den udbrede sig x gange hurtigere i horisontal retning, hvilket vil give følgende formel:

hvor r(t) afstanden fra injektionen til dampfronten til tiden t i horisontal retning og den tilsvarende afstand i vertikal retning vil så være r/x. Faktoren x kunne være bestemt ud fra forholdet mellem den vertikale og den horisontale permeabilitet.

Som det ses, kan der på simpel vis udvikles en model, når blot man kender en formel for dampzonens volumen.

3.2 Energibalancemodel med varmetab (Marx-Langenheim)

Marx-Langenheim-modellen antager, at dampzonen udvikles radialt imellem to impermeable lag, hvortil der er et energitab ved varmeledning. Det antages yderligere, at de impermeable lag har en uendelig udstrækning, og at varmeledningen kun foregår i en dimension. I det tilfælde er det muligt at finde en analytisk løsning for varmetabet, som kan kobles med den tidligere viste model for udbredelsen af en radial dampzone. Herved fås følgende formel:

Forudsætningen for at benytte denne model er den samme som for den radiale model, og hvis forudsætningerne er opfyldt vil den være mere præcis, idet der altid vil foregå varmetab til omgivelserne ved varmeledning.

Den væsentligste begrænsning ved energibalancemodellerne er, at de forudsætter, at dampzonen har en bestemt geometri. I forbindelse med terrænnære oprensninger vil den vertikale permeabilitet oftest være betydelig, og man kan ikke antage, at dampen kun strømmer horisontalt. I de tilfælde kan den radiale energibalancemodel og Marx-Langenheim-modellen derfor ikke benyttes. For at beskrive den situation er man nødt til også at betragte dampens strømning, og det er nødvendigt at koble energibalancen med en strømningsligning.