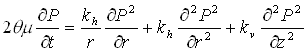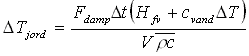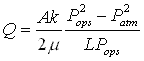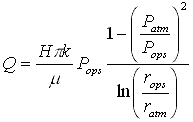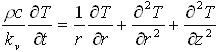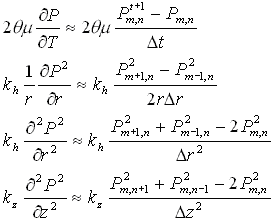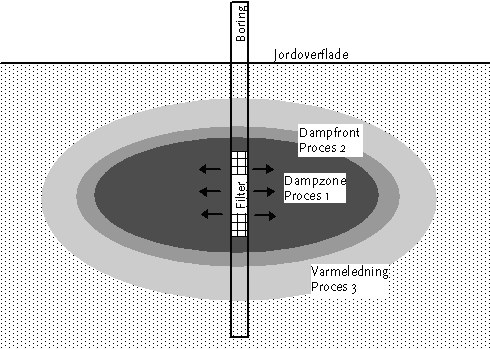
| Forside | | Indhold | | Forrige | | Næste |

Modellering af opvarmning ved dampinjektion (Modi)

4. Modelbeskrivelse

Figur 4.1
Opvarmning af jord ved dampinjektion. Det opvarmede område inddeles i tre zoner afhængigt af, hvilken proces der er den dominerende.

Tæt ved injektionsboringen er jorden opvarmet til damptemperatur, og dampen strømmer i dette område (dampzonen) frem mod dampfronten, hvor den kondenserer og opvarmer jorden. Foran dampfronten foregår der endvidere opvarmning ved varmeledning. I dampzonen vil dampen strømme som en hver anden gasfase, og strømningen er bestemt af permeabiliteten. I den retning, hvor permeabiliteten er størst, vil der strømme mest damp, og dampzonen vil således udbredes hurtigst i denne retning. Varmeledningen foregår uafhængigt af permeabiliteten, men den vil kun have betydning, hvor der er meget begrænset dampstrømning.

I modsætning til energibalancemodellerne kan der ikke findes en analytisk løsning til disse koblede processer, og modellen består af en række styrende ligninger, der løses numerisk.

Situationen på Figur 4.1 illustrerer dampinjektion i den umættede zone, idet dampzonen er vertikalt symmetrisk omkring injektionsfilteret. Modellen kan også håndtere dampinjektion under grundvandsspejlet. I dette tilfælde vil dampzonen bevæge sig mere opad, fordi trykket her vil være lavere.

4.1 Styrende ligninger

De styrende ligninger skal beskrive strømningen af dampen i dampzonen, dampzonens udvikling som følge af kondensation, samt varmeledningen i området foran dampfronten.

Strømning af gasser i porøse medier adskiller sig fra strømningen af vand, idet gassen er mere kompressibel. Vandets kompressibilitet er negligeret i de traditionelle ligninger for grundvandsstrømning, og de skal derfor modificeres for at kunne benyttes til gasstrømning. Antages det, at gassen opfører sig som en idealgas, kan idealgasligningen benyttes til at udtrykke gassens densitet som funktion af trykket, og ved at kombinere denne ligning med Darcys lov og kontinuitetsligningen kan man finde den styrende differentialligning for gasflow. I et to-dimensionelt radialt system bliver ligningen til /6/:

hvor q er den luftfyldte porøsitet, m er dampens viskositet, k_h og k_v er henholdsvis den horisontale og vertikale permeabilitet for gasfasen, P er trykket i gasfasen, t er tiden, r er den axiale koordinat og z er den vertikale koordinat.

Den eneste forskel på denne ligning og den tilsvarende ligning for grundvandsstrømning er, at trykket er kvadreret.

Den næste proces er opvarmningen af jorden ved dampfronten som følge af dampens kondensation og dermed selve dampzonens udvikling. Temperaturstigningen i et volumen jord i løbet af tidsskridtet  kan beregnes ud fra energibalancen ved følgende ligning:

hvor F_damp er fluxen af damp og DT er tidsskridtet. Bemærk, at DT er temperaturforskellen mellem dampen og jordens initielle temperatur, mens DT_jord er temperaturstigningen i jorden i løbet af tiden DT.

Forskellen på denne formulering og de formuleringer der blev anvendt i energibalancemodellerne er, at volumenet V dækker en beregningscelle og ikke hele dampzonen.

Fluxen af damp beregnes ved densiteten og strømningen. Densiteten for dampen er trykafhængig og kan beregnes ud fra idealgasligningen:

hvor M er dampens molvægt, P er trykket, R er gaskonstanten, og T er temperaturen i K.

Indstrømningen af damp kan opdeles i en vertikal og et horisontal del, der kan beregnes analytisk ved steady state /6/:

Disse ligninger giver koblingen mellem strømningsligningerne og energibalancen. Grunden til, at der er forskel på horisontal og vertikal strømning, er, at den horisontale strømning foregår radialt.

Den sidste proces er varmeledning foran fronten. For et to-dimensionelt radialt system har varmeledningsligningen følgende udseende /3/:

hvor k_v er det porøse mediums varmeledningskoefficient og T er temperaturen.

4.2 Løsning af ligninger

Det er ikke muligt at løse ligningerne analytisk, og i stedet benyttes numeriske metoder. Ligningerne diskretiseres og løses ved hjælp af "eksplicit finite difference" teknik. Ved diskretiseringen opdeles det aktuelle jordvolumen i en række ringformede beregningsceller.

Ligningerne for opvarmningen af jorden ved dampfronten beskriver allerede situationen mellem to beregningsceller og skal ikke yderligere diskretiseres.

Den diskretiserede form af de enkelte led i gasstrømningsligningen har følgende udseende:

hvor m angiver cellenummeret i horisontal retning og n angiver cellenummeret i vertikal retning.

Varmeledningsligningen diskretiseres på tilsvarende vis.

Modellens fremgangsmåde er, at den for hvert tidsskridt først beregner trykket i dampzonen, og derefter temperaturstigningen foran dampzonen dels ved kondensation af damp og dels ved varmeledning. I forhold til opvarmningen indstiller trykket sig meget hurtigt, og derfor løses trykligningerne med et mindre tidsskridt, indtil der er opnået stationære forhold. Trykket er således beskrevet ud fra grænsebetingelserne, som er dampzones form og injektionstrykket. I tilfælde af, at dampzonen er udbredt under grundvandsspejlet, vil trykket på grænsen være givet ved vandets tryk, der bestemmes af dybden. Det er beregningsmæssigt den eneste forskel mellem injektion over og under grundvandsspejlet. Grundvandet bliver fortrængt af dampen og ikke opvarmet, og vandet skal derfor ikke indgå i beregningen af varmekapaciteten.

Der er indlagt en ekstra energibalancekontrol, således at temperaturen i et tidsskridt ikke kan stige mere end svarende til den energimængde, der injiceres. Herved undgås en akkumulerende fejl, der kan opstå, eftersom modellen først beregner trykket ud fra injektionsraten, og derefter temperaturstigningen ud fra trykket.