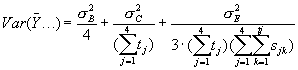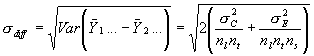| Forside | | Indhold | | Forrige | | Næste |

Effekter af sprøjtemiddelafdrift på bærbærende buske og træer som indikator for biodiversitetsforandringer

2. Prøvestørrelser

2.1 Introduktion

Det er intentionen i dette afsnit at estimere det nødvendige prøveantal for forskellige målvariable ved hjælp af statistiske styrkeberegninger. Som forberedelse til et forsøg kan man udfra en kendt variation på måleparameteren, det ønskede signifikansniveau og den ønskede statistiske styrke beregne hvor mange prøver der skal indsamles. En forudsætning for at dette også fører til et godt statistisk funderet materiale er, at alle betydende faktorer for variansen er kendt. Et sådant variansskøn vil være et estimat, og det er derfor muligt at man til trods for en udregning af det nødvendige prøveantal ender med en lav statistisk styrke. Dette vil ske hvis enten forforsøget eller hovedforsøget gennemføres under atypiske forhold (abiotiske såvel som biotiske). Den forberedende styrkeberegning vil øge sandsynligheden for at få en statistisk god test. Det er vigtig at fastslå at statistisk signifikans ikke nødvendigvis er ensbetydende med biologisk relevans. I enhver test er det vigtigt at den der planlægger og gennemfører forsøget forholder sig til den "relevante effektstørrelse".

2.2 Metode

2.2.1 Indsamlinger

Der blev indsamlet blade, blomster og bær af tjørn fire gange gennem plantens fænologiske udvikling. Første indsamling blev fortaget den 30. maj hvor tjørnen havde udfoldet årsskuddets blade og der var blomsterknopper til stede. Anden høst blev foretaget 14. juni, hvor alle blomsterne var færdigudviklede. Første bærhøst blev indsamlet den 6. august, og der blev siden foretaget en efterårsindsamling af bær. Sidst i august blev de grene der skulle høstes i efterårsperioden udvalgt tilfældigt og en netpose (maskestørrelse på 1mm) blev monteret for at forhindre fugle i at spise bærrene. Disse bær blev høstet den 22. oktober.

Ved hver høst blev der indsamlet blad-, blomster- eller bærskud fra fire tjørnehegn beliggende nord for Silkeborg (jordbundsbeskrivelse findes i Bilag A). Der blev indsamlet fra fem tilfældigt udvalgte træer i hvert hegn. I hvert træ blev ovennævnte skudtyper indsamlet fra grene i 1, 3 og 5 meters højde. For hver højde blev der høstet mellem 1 og 10 sideskud. De lave antal indsamlinger forekom når den givne skudtype ikke var at finde i det givne træ i den givne højde. Indsamlingsprogrammet er gengivet i Tabel 2.1. Tjørns sideskud kan enten være langskud eller kortskud. Kortskuddene kan bære både blomster og blade, mens langskuddene udelukkende bærer blade.

Tabel 2.1
Tabel over indsamlinger i usprøjtede hegn.

Der blev udvalgt fem hegn til at bestemme variationen i blad, blomster og bærproduktion i hegn der ikke var eksponeret for sprøjtemidler. Det viste sig dog at en af markerne til trods for dette var blevet sprøjtet. Dette hegn, benævnt A, blev herefter taget ud af undersøgelserne. De resterende hegn i henholdsvis Buskelund og på Sinding Hedevej (nordlige Silkeborg) er afmærket på nedenstående luftfotos taget i 1995 (Figur 2.1- 2.3).

Figur 2.1
Luftfoto af de to hegn (B og C) fra Buskelund. (Kilde: Danmarks Digitale Orthofoto 1995/Kampsax 1995).
    

Figur 2.2
Luftfoto af hegn D på Sinding Hedevej. (Kilde: Danmarks Digitale Orthofoto 1995/Kampsax 1995).
    

Figur 2.3
Luftfoto af hegn E på Sinding Hedevej. (Kilde: Danmarks Digitale Orthofoto 1995/Kampsax 1995).

2.2.3 Beregning af varianskomponenter

Der blev opstillet følgende hierakiske statistiske model som indeholder alle komponenter af variationen for de enkelte undersøgte responsvariable:

, (1)

hvor Y er den analyserede responsvariabel. Indeks i står for niveau (i=1, 2, 3), j for læhegn (j=1, 2, 3, 4), k for trænummer i et givent læhegn (k=1, 2,..., tj) og l for sideskud i et givet træ (l = 1, 2, ...., s_jk). B_j er varianskomponenten for læhegn, C_jk er varianskomponenten for træer i et givent hegn og D_jki er varianskomponenten for niveauer i et givet træ og et givet læhegn. Endelig er E_ijkl fejlleddet (det vil sige variansen mellem sideskud). Vi antager, at

B_j ~ N (0,) , C_jk ~ N (0,) , D_ijk ~ N (0, ), samt E_ijkl ~ N (0,).

Desuden antages, at de enkelte stokastiske variable er indbyrdes uafhængige. Med disse antagelser er:

hvor står for gennemsnittet af Y, det vil sige

.

Vi har bestemt os for at udføre styrkeberegningerne i kun et niveau nemlig mellemhøjden, idet det vil være mere resourcekrævende at indsamle i højeste niveau og fordi hovedparten af sprøjtemiddelafdriften afsættes i de nederste dele af hegnet.

Dermed anvendes følgende model :

, (2),

hvor B_j ~ N (0, ) , C_jk ~ N (0, ) , E_jkl ~ N (0, ) og E_jkl står for fejlleddet.

I denne model er

,

Varianskomponenterne ,  og estimeres ved REML-metoden ved anvendelse af Proc Mixed i SASÓ (Verbela & Molenberghs 1997).

2.2.4 Beregning af styrke

Den statistiske model som er blevet benyttet ved styrkeberegningerne er

(3),

hvor vi antager at C_ijk ~ N (0,) , E_ijkl~ N (0,), og indeks i står for behandling , j for læhegn, k for trænummer i et givent læhegn og l for sideskud i et givet træ (i=1,..., n_b, j=1,..., n_l k=1,..., n_t og l=1,..., n_s). Det vil sige at modellen ikke indeholder niveau og vi antager at effekten af læhegn ikke er tilfældig. Det vil sige at inddeling efter behandling og læhegn udgør et 2-sidet skema hvor der er n_t ´ n_s observationer i hver celle.

I vores rapport har vi antaget at hegn er en systematisk effekt. I den statistiske analyse er det muligt både at antage en systematisk eller en tilfældig effekt af hegn. Argumentet for at vælge hegn som en tilfældig faktor er, at de hegn som medtages i projektet er et tilfældigt udtag (random sample) af alle mulige hegn af en bestemt type. Generalisering til alle hegn af denne type er mulig men kun ved et udtag af et større antal hegn. Argumentet for at betragte hegn som en systematisk faktor kan være at man er interesseret i at teste forskelle mellem de enkelte hegn. Denne angrebsvinkel egner sig bedst til undersøgelser med få hegn. Generalisering er ikke direkte opnåelig. Konsekvensen af at vælge at effekten af hegn er tilfældig er at variansen på forskellen mellem to behandliger øges og hermed øges også kravet til antal prøver.

Ved styrkeberegningerne ønskes at kunne påvise en forskel på d mellem to givne behandlinger på et 5% signifikansniveau ved en ensidig test. Den ene behandling kan i dette tilfælde være kontrolbehandlingen, det vil sige ingen sprøjtning. Vi har valgt d = 20% i de udførte beregninger.

Antager vi ingen vekselvirkning mellem læhegn og behandlinger (ab_ij = 0), så er spredningen på differensen mellem to behandlinger lig

, (4),

hvor
n_l: antal læhegn
n_t: antal træer
n_s: antal sideskud

Interaktioner mellem hegn og behandling kan forekomme fordi: 1) hegnene har forskellig struktur og hermed er der forskelle i sprøjtemiddelafsætningen, 2) de abiotiske forhold er forskellige mellem sprøjtningerne i de enkelte hegn eller 3) fordi hegnene er genetisk og aldersmæssigt forskellige. Antagelsen om ingen vekselvirkning mellem læhegn og behandlinger bygger på følgende: 1) forskellen i afsætning vil ikke påvirke analysen idet vi måler afsætningen det samme sted som prøvetagningen foregår. 2) de forskelle der vil være ved sprøjtningen er negligerbare i forhold til de effekter vi ønsker at dokumentere og endelig vil genetiske og aldersmæssige effekter være beskrevet af den systematiske effekt.

Størrelsen s _diff kan beregnes ved at anvende estimater forog   fundet ved anvendelse af formel (2).

På baggrund af beregninger som præsenteret ovenfor ønsker vi at beregne det antal prøver der er nødvendige for statistisk at kunne dokumentere en 20% forandring af den enkelte responsvariabel.

Projektet sigter på at etablere en dosis – respons sammenhæng for de enkelte responsvariable, men vælger at basere styrkeberegningerne på en t-test for ikke at være afhængig af en række doser der rammer inden for intervallet af 20 til 90% effekt. Hermed bliver vi, med det valgte prøveantal, i stand til at opnå en høj styrke selv med kun en brugbar testdose. Skulle testdoserne alle ligge i effektområdet mellem 20 og 90%, vil en regressionsanalyse, der har samme eller større statistisk styrke end en t-test, blive anvendt.

Styrkeberegningen blev gennemført for en ensidig t-test, fordi vi kun interesserer os for negative effekter af herbicidafdrift. Beregningen tog udgangspunkt i at vi ønsker at indsamle så mange prøver at vi kan detektere effekter (d ) på 20% eller derover med en statistisk styrke på 80% eller mere.

Styrken beregnes ved sandsynligheden:

styrke = P(t_u,t ³ t_u (0,05))

Det vil sige at sandsynligheden for at t_u,t i en ikke-central t-fordeling med parametrene t og u er større end den kritiske t-værdi med u frihedsgrader.

Parametrene u og t er:

u = 2 n_l (n_t-1), bemærk at træ er forsøgsenheden,

, er ikke centralitetsparameter i den ikke-centrale t-fordeling

Vi har valgt at anvende n_l: 1, 2, 4, 8 eller 16; n_t: 2, 3, 4,....29; n_s: 1, 3, 5, 10 eller 20.

2.3 Resultater

2.3.1 Varianskomponenter

I nedenstående Tabel 2.2 findes varianskomponent-estimaterne til ovenstående model (2).

Tabel 2.2
Tabel over de estimerede varianskomponenter for formel (2) for forskellige måleparametre. Data er transformeret; ved antal anvendes og ved vægt anvendes log(x). Tabelværdier på 0 fremkommer fordi nogle analyser gav negative varianskomponenter og dette er ikke logisk muligt.

Tabel 2.3
Tabel over middelværdien af forskellige måleparametre i mellemniveau. n er antallet af obervationer. im betyder: ikke målt.

  
2.3.2 Statistisk styrke

Den statistiske styrke blev beregnet for en række måleparametre ved forskellige prøvetagningsscenarier. Som tidligere nævnt har vi valgt følgende scenarier: Hegn (n_l): 1, 2, 4, 8 eller 16; træer (n_t): 1, 2, 3, 4,....29; og sidegrene (n_s): 1, 3, 5, 10 eller 20 gennemført i alle kombinationer. Nedenfor er resultatet for sådanne styrkeberegninger præsenteret i Figur 2.3. Figuren er lavet på basis af data for grønne bær og vi har udvalgt de kombinationer hvor antallet af træer er 1, 2, 3, 4, 5, 6, 10, 15, 20, 25 og 29 for at forbedre læsbarheden af figuren.

Figur 2.4
Relationen mellem det antal sidegrene der høstes fra hver træ og den resulterende statistiske styrke for antal grønne bær. Delfigurerne (A, B, C, D og E) repræsenterer prøvetagninger i henholdsvis 1, 2, 4, 8 eller 16 hegn.

Nedenfor findes tabeller over det nødvendige prøveantal for at vi kan detektere effekter (d ) på 20% eller derover med en statistisk styrke på mindst 80% for forskellige responsvariable. Tabellerne 2.1 til 2.4 præsenteres således at hvert enkelt måleparameter præsenteres i forhold til deres placering i den fænologiske udvikling (blad, knopper, blomster, bær og modne bær). I tabellerne er der også opgjort det samlede antal prøver der skal indsamles og bearbejdes.

Bladene blev høstet fra både kort- og langskud. Da disse skudtyper er morfologisk forskellige holdes de adskilt i styrkeberegningen. Der var blevet målt både antal blade i et sideskud og den samlede vægt af bladene i sideskuddet (biomasse). For responsvariablen "Antal" (antallet af blade i det enkelte sideskud) var det muligt at opfylde de givne kriterier (påvise en effekt på 20% med et 5% signifikansniveau og en statistisk styrke på 80%) ved indsamlinger i 1,2,4, 8 eller 16 hegn (Tabel 2.4). For både kortskud og langskud viste det sig at der skulle samles færre prøver hvis der kun bliver høstet en sidegren per træ. Endvidere krævede kortskud flere prøver end langskud. For responsvariablen "Biomasse" kunne der ikke inden for vores scenarier opnås en statistisk styrke på 80% for kortskud, hvis der kun blev indsamlet prøver i et enkelt hegn. Det samme gjorde sig gældende for 2 hegn og 1 sideskud. For de øvrige kombinationer var det muligt at opnå en statistisk styrke på 80%. Igen var det tydeligt at det samlede prøveantal var lavest med de færreste høstede sidegrene, men der var ingen større forskelle mellem antal af testhegn.

Tabel 2.4
Tabel over antal træer der er nødvendige i det enkelte hegn for at kunne påvise en effekt på 20% med et 5% signifikansniveau og en statistisk styrke på 80% når antallet af sidegrene og antallet af hegn er givet. Måleparametrene er antallet eller biomassen af blade på henholdsvis kortskud og langskud. im betyder at det ikke var muligt at opnå en statistisk styrke på 80% med de kombinationer af #hegn, #træer og #sidegrene vi har valgt. "Prøver" er det antal prøver der i alt skal analyseres (#hegn ´ # træer ´ # sidegrene). De skraverede felter angiver den kombination der resulterer i færrest prøvetagninger.

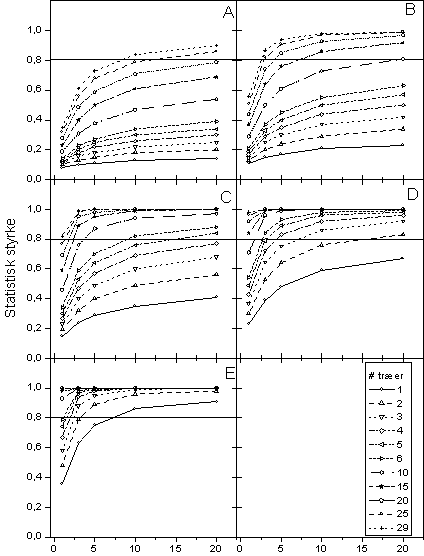
For at påvise en 20% effekt på enten antallet eller biomassen af knopper i et sideskud viser de styrkeberegninger der er præsenteret nedenfor (Tabel 2.5), at det ikke er muligt at nøjes med at høste 1 sidegren per træ i 1 hegn. For alle de øvrige kombinationer var det muligt at opnår den ønskede styrke. Antallet af prøver er lavest når der høstes få sidegrene i hvert træ. Responsvariablen "Biomasse" var generelt mere variabel og krævede dermed også flere prøver. Der var kun små forskelle mellem antal testhegn.

Tabel 2.5
Tabel over antal træer der er nødvendige for at kunne påvise en effekt på 20% med et 5% signifikansniveau og en statistisk styrke på 80% når antallet af sidegrene og antallet af hegn er givet. Måleparameteren er antallet eller biomassen af blomsterknopper. im betyder at det ikke var muligt at opnå en statistisk styrke på 80% med de kombinationer af #hegn, #træer og #sidegrene vi har valgt "Prøver" er det antal prøver der i alt skal analyseres (#hegn ´ # træer ´ # sidegrene). De skraverede felter angiver den kombination der resulterer i færrest prøvetagninger.

Det var kun antallet af blomster der blev registreret. Vægten kunne ikke registreres fordi mange af blomsterne havde tabt deres kronblade under prøvetagning og prøvebehandling. Ud fra data på antal blomster viste den statistiske styrkeberegning, at det ikke var muligt at opnå en statistisk styrke på 80% hvis der indsamles hhv. 1 eller 3 sideskud fra træer i et enkelt hegn (Tabel 2.6). For de øvrige scenarier kunne den statistiske styrke opnås. Antallet af indsamlinger var lavest ved indsamlinger et enkelt sideskud per træ og sammenlignelig mellem 2, 4, 8 eller 16 testhegn.

Tabel 2.6
Tabel over antal træer der er nødvendige for at kunne påvise en effekt på 20% med et 5% signifikansniveau og en statistisk styrke på 80% når antallet af sidegrene og antallet af hegn er givet. Målepareameteren er antallet blomster. im betyder at det ikke var muligt at opnå en statistisk styrke på 80% med de kombinationer af #hegn, #træer og #sidegrene vi har valgt. "Prøver" er det antal prøver der i alt skal analyseres (#hegn ´ # træer ´ # sidegrene). De skraverede felter angiver den kombination der resulterer i færrest prøvetagninger.

Denne styrkeberegning (Tabel 2.7) viser, at for at påvise en 20% effekt på antallet af bær i et sideskud skal vi for at opnå en statistisk styrke på 80% for begge responsvariable indsamle mindst 10 sideskud i hvert af 26 træer i et enkelt hegn. I 2 hegn skal der mindst indsamles 3 sideskud per træ (Tabel 2.6). Ellers er mønsteret som for de øvrige endpoints (blade, knopper og blomster) at det giver færrest indsamlinger at høste en sidegren per træ. Som det også fremgår af tabellen skal der tages færrest prøver ved at indsamle 1 sidegren fra hvert af 13 træer i hvert af 8 hegn.

Tabel 2.7
Tabel over antal træer der er nødvendige for at kunne påvise en effekt på 20% med et 5% signifikansniveau og en statistisk styrke på 80% når antallet af sidegrene og antallet af hegn er givet. Måleparameteren er antallet eller biomassen af grønne bær. im betyder at det ikke var muligt at opnå en statistisk styrke på 80% med de kombinationer af #hegn, #træer og #sidegrene vi har valgt. "Prøver" er det antal prøver der i alt skal analyseres (#hegn ´ # træer ´ # sidegrene). De skraverede felter angiver den kombination der resulterer i færrest prøvetagninger.

  
2.3.2.5 Modne bær

Med de begrænsninger vi har sat for vores styrkeberegninger, dvs. for at opnå en statistisk styrke på 80% for vægten af de modne bær i sideskuddet skal der i et enkelt hegn indsamles 20 sideskud per træ i 29 træer. I 2 hegn skal der mindst indsamles 3 sideskud per træ i 26 træer. For 4, 8, og 16 hegn er alle kombinationer mulige. Prøvetallet minimeres ved at høste så få sideskud per træ som muligt. Responsvariablen "Antal" er er den mest variable for de modne bær. For de modne bær angiver beregningerne at der skal samles færrest prøver hvis der bliver indsamlet 1 sidegren fra hver af 13 træer i hvert af 8 hegn eller 1 sidegren fra hvert af 26 træer i hvert af 4 hegn.

Tabel 2.8
Tabel over antal træer der er nødvendige for at kunne påvise en effekt på 20% med et 5% signifikansniveau og en statistisk styrke på 80% når antallet af sidegrene og antallet af hegn er givet. Måleparameteren er antallet og biomassen af modne bær. im betyder at det ikke var muligt at opnå en statistisk styrke på 80% med de kombinationer af #hegn, #træer og #sidegrene vi har valgt. "Prøver" er det antal prøver der i alt skal analyseres (#hegn ´ # træer ´ # sidegrene). De skraverede felter angiv er den kombination der resultere i færrest prøvetagninger.

2.4 Konklusioner for kommende forsøg

De ovenstående styrkeberegninger viser entydigt at antallet af prøver bliver lavest når der høstes få sideskud per træ, men at det selvfølgelig kræver tjørnehegn med flere træer hvilket selvsagt begrænser antallet af egnede lokaliteter. Derudover er der andre omkostninger ved at tage prøver i flere hegn. Der følger en omkostningsberegning i Kapitel 6.
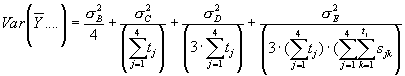
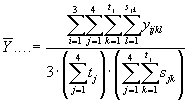