Modellering af optagelse af organiske stoffer i grøntsager og frugt
Bilag B
The "Carrot Model"
The "Carrot model" is a flux-based dynamical equation, which is solved for the steady-state (Trapp 2002). It considers advective influx with the transpiration stream as input, and outflux and metabolism as output. Dilution by growth may occur. Diffusive uptake is assumed to be restricted to the peel, which is not consumed. This assumption has been shown to be valid for very lipophilic compounds such as benzo(a)pyrene and PCB (Trapp 2002).
The assumption of chemical equilibrium is probably justified for thin roots (Trapp 1995), but not necessarily for thick roots, because the diffusive flux is proportional to the surface area. In particular for thicker roots and lipophilic chemicals, real concentrations can be far below chemical equilibrium. This means, that in the risk assessment process, risk from uptake of lipophilics into roots is currently probably overestimated. Therefore, a new, flux based approach was developed (Trapp 2002).
The value of KRW which is used in this model differs in units and parameterization and is
| KRW = W + L a KOW b | Equation 9 |
where
| W | is the water content (mass per mass) |
| L | is the lipid content (mass per mass), |
| b | is 0.77 (Briggs’ value for roots) |
| a | is a factor correcting density differences between water and n-octanol (1.22). |
If only the peel of a root vegetable is in diffusive exchange with the surrounding soil,
the core is loaded solely with the water taken up. Then, for this core, uptake is with the
transpiration stream Q (L/d) and loss is by flux upward and metabolism kE,Root
(d-1):
| dmR/dt = d(V× CR)/dt
= kG,root× V× CR+V× dCR/dt = CW× Q - CXY× Q – kE,Root× V× CR |
Equation 10 |
where
| mR | is the mass of chemical in roots |
| CW | is the concentration in the soil solution, calculated as described (mg/L). |
| CXY | is the concentration in the xylem (mg/L) at the outflow of the root. If the xylem sap is in equilibrium with the root, CXY is CR/KRW; kE,Root is a first order metabolic rate. |
| V | is the volume of the root. The volume is assumed to increase exponentially with time with the rate constant kG,Root. |
The steady-state solution for the dynamic (steady-state) bioconcentration factor between
root core and soil solution BCF(W) is
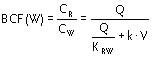 |
Equation 11 |
where
| k | is the sum of kG,Root and kE,Root |
| V | is the root volume (L) |
In the absence of metabolism and growth (k = 0), the concentration ratio CR/CW
equals the thermodynamic equilibrium KRW.
The ratio between the concentration in root and soil is simply obtained by multiplication with the factor fW = CW/CSoil
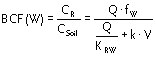 |
Equation 12 |
A default parameterization of the equation is listed in Table B.1.
Limitations
The model approach is strictly limited to non-ionizing and lipophilic compounds with a low vapour pressure, and to peeled root vegetables. Only for the compounds with a log (KOW/KAW) > 8, diffusion through the peel into the core can be neglected. This holds, e.g., for PCB and PCDD/F with more than four chlorine, benzo(a)pyrene, fluoroanthene and six-ring PAH, but not for benzene and naphthalene, and not for hexane, octane, dodecane.
Table B.1
Default parameters of the carrot model (Trapp 2002)
Parameter |
Symbol |
Value |
Unit |
Root water content |
W |
0.89 |
g/g |
Root lipid content |
L |
0.025 |
g/g |
Density correction |
a |
1.22 |
(-) |
Empirical factor |
b |
0.77 |
(-) |
Transpiration stream |
Q |
1 |
L/d |
Root volume |
V |
1 |
L |
1st order rate |
k = kG,Root + kE, Root |
0.1 |
d-1 |
Sensitivity analysis
Figure B.1 shows the result of this new flux based root uptake equation with varying loss rate k (0.1 and 0.01 d-1 corresponding to a half time of 6.9 and 69 days) and log KOW of the chemical. It can be seen that for chemicals with low or intermediate lipophilicity (log KOW < 2), the difference between equilibrium partitioning (k = 0) and dynamic uptake equation is negligible. However, for the more lipophilic compounds, the difference is considerable, in particular for higher k values.
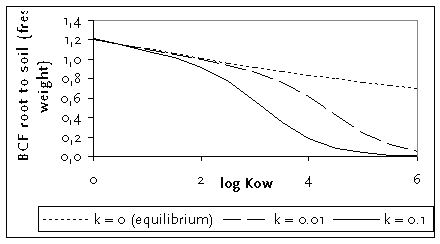
Figure B.1
Bioconcentration factor roots (fresh weight) to soil matrix simulated with the dynamic
approach versus log KOW for three values of k. Calculations made without
chemical in the water fraction of roots and soil.