Modellering af optagelse af organiske stoffer i grøntsager og frugt
Bilag D
Fruit Tree Model
The tree model considers chemical influx into stem via xylem, outflux after equilibration, dilution by growth and first order metabolism (Trapp 2001). Exchange with air is neglected. The main difference between herbs or vegetables trees is the big wood compartment of trees with a mass of up to several hundred tons per ha. Wood is composed of cellulose, hemicellulose and lignin, which is a giant macromolecule with lipophilic sorption properties. The concentration ratio between wood and water named "KWood,W" (mg chemical per g dry wood to mg chemical per ml water) is significantly correlated to the log KOW, for oak (Trapp et al. 2001):
| log KWood,W = – 0.266 (± 0.25) + 0.632 (± 0.063) log KOW (n=27, r=0.90) | Equation 19 |
Mass balance for the stem
| Influx | Q · CXY | Equation 20 |
| Sinks | kE× m + Q · CStem /KWood = kE ·
M · CStem + Q · CStem
/KWood |
|
| Change in mass in the stem | dm/dt = M · dCStem/dt
+ CStem · dM/dt = M · dCStem/dt + CStem · kG · M |
|
| Mass balance equation | M · dCStem/dt = Q · CXY - Q · CStem
/KWood - kE · M · CStem - CStem ·
kG · M or dCStem/dt = (Q/M) · CXY – (Q/M) · CStem /KWood – (kE + kG) · CStem |
Steady-state solution (dCStem/dt = 0):
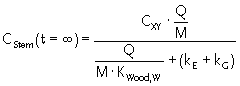 |
Equation 21 |
where
| m | is mass of the chemical in the stem |
| CXY | is the concentration of chemical in xylem sap. CXY is estimated from the concentration in soil solution CW by: CXY = TSCF · CW |
| CStem | is the concentration of chemical in stem |
| kG | is the stem growth rate constant, which is set to 0.01 year-1 in the calculations |
| kE | is the first order metabolism rate constant (0.692 years-1) |
| Q | is the transpiration of the fruit tree stand (approx. 3000 m3 ha-1 year-1) and |
| M | is the stem wood mass (100 t ha-1). |
The transpiration stream concentration factor (TSCF) is calculated by the correlation of
Burken & Schnoor (1998) for poplars (corrected):
| TSCF = 0.756 · exp [- (log KOW - 2.50)2 / 2.58] | Equation 22 |
The calculated concentration ratio between stem and bulk soil with and without metabolism
is shown in Table D.1. Chemicals with a low or medium log KOW have a potential
to accumulate in significant amounts in the stem via xylem from soil. Very lipophilic
chemicals have low steady-state concentrations in stem compared to the soil concentration,
due to slow uptake and dilution by growth. If chemicals are metabolized in wood, chemicals
with slow uptake (high lipophilicity) will decrease in concentration. The half-life of 1
year is given to illustrate that even slow rates can lower steady-state concentrations of
the lipophilic compounds in wood significantly.
Table D.1
Calculated steady-state concentration ratio between the concentration in the
stem of an oak and bulk soil for different metabolism half-lives. 2% organic carbon in
soil assumed.
Compound |
CStem/CB
|
CStem/ CB
|
Naphthalene |
3.61 |
1.37 |
Benzo(a)pyrene |
4.14 · 10-3 |
1.01 · 10-4 |
MTBE |
2.97 |
2.79 |
Toluene |
5.89 |
3.51 |
n-Dodecane |
1.45 · 10-2 |
4.45 · 10-4 |
Trichloroethene |
4.90 |
2.43 |
Benzene |
6.66 |
5.22 |
Tetrachloroethene |
5.46 |
3.02 |
Concentration in fruit
Transport into fruits can occur both with the phloem sap and with the xylem sap. In fruits, all dry mass arrives via the phloem. Phloem sap has a high dry mass content, about 10%. This dry mass remains in the fruit. Therefore, we can assume that the phloem flow is approximately 10 times the dry mass content. Different to leaves, fruits do not transpire very much, approximately the same amount of water is additionally flowing to the fruit via the xylem, to replace water evaporated from the peels. Table D.2 gives the dry mass content of a number of fruits from trees (Elmadfa et al. 1991), and the calculated water flow per kg fruit (fresh weight).
| QW = dw · 20 | Equation 23 |
where
| QW | is the water flow into 1 kg of fruit |
| dw | is the dry weight fraction of the fruit. |
Although phloem loading with sugars occurs in the leaves, phloem concentrations of
nonionized chemicals change toward the equilibrium with the stem. Thus the concentration
of the chemical in the phloem sap is assumed to be the same concentration as within the
xylem sap, which is calculated assuming chemical equilibrium between xylem and xylem sap.
The amount of chemical m transported with this water can then be calculated from the concentration in stem:
| m= QW× CStem /KWood,W | Equation 24 |
The concentration is then obtained by dividing the chemical mass m by the weight of the
fruit (1 kg).
Table D.2
Dry weight of popular Danish fruits, and estimated water flow per kg fresh
fruit
Fruit |
Water content |
Dry mass |
Water flow |
Hazelnut |
5.6% |
94.4% |
18.88 |
Walnut |
5.0% |
95% |
19 |
Apple |
85.7% |
15.6% |
2.86 |
Blackberry |
84.6% |
15.4% |
3.08 |
Cherry |
81.6% |
18.4% |
3.68 |
An example calculation for a fruit tree stand with 100 tons/ha biomass and 300 mm/year
transpiration, a metabolisation half-life of one year of the chemical, and the water flux
for nuts (19 L water flux per kg fruit) or apples (3.12 L water per kg fruit) is shown in
Table D.3.
Calculated concentrations in fruit are rather high for the polar compounds, but probably overestimated. The model can be considered as "conservative", because loss of compound from the stem and the fruit by volatilization into air and by metabolism in the fruit is neglected.
Table D.3
Calculated bioconcentration in fruits (mg/kg fresh fruits : mg/kg wet soil).
2% organic carbon in soil
Compound |
Apple |
Hazelnut |
Naphthalene |
0.05 |
0.36 |
Benzo(a)pyrene |
7.14 · 10-8 |
4.71 · 10-7 |
MTBE |
2.80 |
18.5 |
Toluene |
0.34 |
2.23 |
n-Dodecane |
5.07 · 10-7 |
3.35 · 10-6 |
Trichloroethene |
0.16 |
1.03 |
Benzene |
1.24 |
8.19 |
Tetrachloroethene |
0.25 |
1.62 |