Modellering af optagelse af organiske stoffer i grøntsager og frugt
Bilag F
Soil-Air-Plant transport model SAP
Besides the simple assumption of chemical equilibrium between chemical concentration in soil, lower atmosphere, and plant, only one modelling attempt has been made to develop a model for diffusive transport of compounds in the vapour phase from soil to atmosphere (Trapp & Matthies 1997). The model calculates volatilization from soil by a solution of the diffusion equation for two neighbouring media with different properties. Within soil and vegetation layer, immediate equilibrium between gas phase and soil matrix or plant material is assumed, and an effective diffusion coefficient is calculated.
The mathematical solution is based on the following rigid boundary conditions:
Soil (z<0)
| C = | total concentration in bulk soil = CB |
| D = | effective gaseous diffusion coefficient of the gaseous fraction in soil = DA,eff× fA = DB |
Initial condition: semi-infinite contaminated soil, CB(t=0, z<0) = constant = CB(0)
Vegetation (z>0)
| C = | concentration in vegetation layer = CV |
| D = | diffusion coefficient in the vegetation layer: D = DV |
initially clean vegetation: CV(t=0, z>0) = constant = 0
At the soil surface (z=0), the concentration is in local equilibrium, described by the partition coefficient K:
| K = KVR = CV(z=0)/CB(z=0) | Equation 30 |
At the boundary, the flux out of the soil is equal to the flux into the vegetation (and
vice versa):
| Equation 31 |
For this problem, Jost found already in 1937 a standard solution:
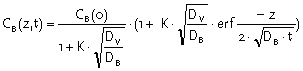 |
Equation 32 |
and
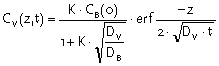 |
Equation 33 |
A few cms above the soil surface, dispersion dominates over diffusion, and turbulence leads to a quick mixing with the lower atmosphere (Nobel 1991). To account for this effect, the concentration in the plant due to volatilization from zero cm to growth height can be integrated. Concentrations in plant parts >5 cm, where the air is turbulently mixed, are better calculated from equilibrium to the lower atmosphere (see Figure F.1).
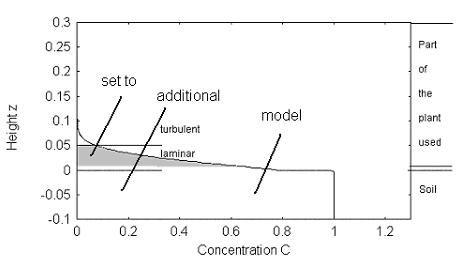
Figure F.1
Calculation of chemical mass transfer in gas phase transport with the
soil-air-plant model, where C = the concentration in soil or vegetation minus equilibrium
concentration to air.
The approach has been used and tested by Thomas et al. (1998) to calculate the air-pasture transfer of polychlorinated biphenyls. The authors compared measured and modelled concentrations for different heights. Best agreement was found when the simulated concentration was averaged for the plant from soil surface to 5 cm height. For the PCB congener 52, 1.2 pg/g grass were predicted, but 44 pg/g were measured. For PCB 153, 55 pg/g were predicted, and 66 pg/g measured. For PCB 180, 26 pg/g were predicted, but 40 pg/g were measured. The authors concluded that the model assumptions are unrealistic. But the strict initial and boundary conditions are necessary to obtain the mathematical solution.