Diffus jordforurening og kulturlag
Bilag A
Deskriptiv statistisk analyse af koncentrationen af bly, kobber, zink samt PAH i jordprøver udtaget fra Nyboder.Deskriptiv statistisk analyse af koncentrationen af bly, kobber, zink samt PAH i jordprøver udtaget fra Nyboder.
Marts 2003
1.1 Formål
Formålet med nærværende analyse er at belyse relationer/korrelationer mellem koncentrationen af Bly, Kobber, Zink, og PAH.
1.2 Analyse
I det følgende foretages en statistisk analyse af de beskrevne data. Først beskrives en række elementer der indgår i analysen. Beregning af: "Skewness" beskriver graden af symmetri, eller afvigelse fra symmetri i en fordeling. Skewness beregnes ud fra anden og tredje ordens momenter i fordelingen og en positiv værdi indikerer en lang hale til højre og negative værdier indikerer en lang hale til venstre. Værdier omkring 0 indikerer en næsten symmetrisk fordeling.
"Kurtosis" beskriver graden af "peakness", dvs. højden af fordelingen i forhold til bredden. En høj værdi indikerer at der er en høj top i centret af data og en lille værdi at der er en bred top i centret af data.
I forbindelse med normalfordelings fraktilplot (Q-Q-plot):
| "U-form" | af Q-Q-plottet indikerer at den ene fordeling er skæv i forhold til den anden. |
| "S-form" | indikerer at fordelingen har længere haler end den anden. I forhold til normalfordelingen betyder det at hvis fordelingen i Q-Q-plottet bøjer ned til venstre og op til højre er halerne længere end normalfordelingens. |
Til at test normalfordelings antagelser anvendes Shapiro-Wilks test (W) for normalitet. W er attraktiv fordi den har en simpel grafisk fortolkning. Man kan tænke på den som at approksimativt mål for korrelationen i et normalfordelingsplot.
Yderligere betragtes Kolmogorov-Smirnov (KS) der tester hypotesen at alle observationer stammer fra en normalfordeling mod alternativet at bare en af observationerne ikke kommer fra fordelingen. I normalfordelingstilfældet er (W) et stærkere test end (KS).
1.3 Ikke-transformerede data
Først indledes med deskriptiv statistik, jf. tabel A.1
| Bly | PAH | Kobber | Zink | |
| Minimum | 23 | 0,0025 | 8,2 | 55 |
| 1. Kvartil | 136 | 0,79 | 53 | 242 |
| Gennemsnit | 389 | 2,69 | 84 | 554 |
| Median | 355 | 1,79 | 81 | 500 |
| 3. kvartil | 516 | 2,96 | 110 | 826 |
| Max: | 2665 | 21,8 | 310 | 1370 |
| Antal | 50 | 50 | 50 | 50 |
| Nedre konfidensgrænse: | 275 | 1,45 | 70 | 446 |
| Øvre konfidensfrænse | 502 | 3,92 | 99 | 662 |
| Skewness | 3,9 | 3,71 | 1,8 | 0,59 |
| Kurtosis | 21,4 | 17,17 | 76,4 | -0,76 |
Tabel A.1 Deskriptiv statistik
Det ses umiddelbart for Bly PAH og kobber at middelværdi og median er væsentligt forskellige samt at fordelingerne er højreskæve (lang højre hale, skewness er positiv, kurtoisis stor). Dette er ikke tilfældet for Zink
Korrelationen mellem de enkelte variable er vist i tabel A.2.
| Bly | PAH | Kobber | Zink | |
| Bly | 1,00 | 0,19 | 0,22 | 0,37 |
| PAH | 0,19 | 1,00 | 0,32 | 0,46 |
| Kobber | 0,22 | 0,32 | 1,00 | 0,55 |
| Zink | 0,37 | 0,46 | 0,55 | 1,00 |
Tabel A.2 Korrelation
Illustreret grafisk i figur A.1, der ses størst korrelation mellem zink og kobber. Der ses enkelte afvigende værdier (outliers).
I figur A.2 og A.3 vises normalfordelings-fraktilplot. Der ses afvigelser fra normalfordelingen for alle 4 variable.
Figur A.1 Korrelationsplot
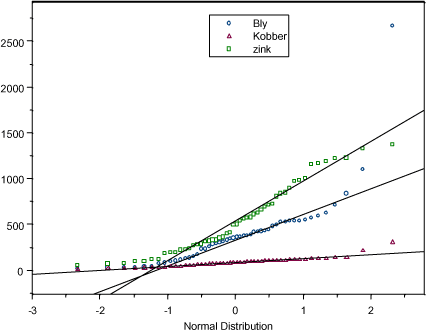
Figur A.2 Normalfordelings-fraktilplot: bly, kobber og zink
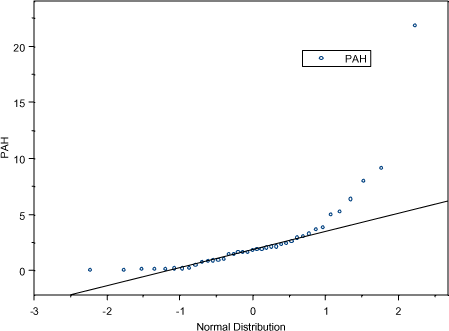
Figur A.3 Normalfordelings-fraktilplot: PAH
En anden måde at illustrere normalfordelings antagelserne er ved at plotte de kumulerede fordelinger for data og den tilhørende normalfordeling med parametrene middel og varians fra data, jf. figur A.4.
Figur A.4 Kumulerede fordelingsplot
Dette afslører ligeledes afvigelser fra normalfordelingen, idet kurverne ikke er sammenfaldende.
Endelig kan det testes om data kan tænkes at stamme fra en normalfordeling.
| Hypotese: | Den sande kumulerede fordeling er en normal fordeling med de estimerede parametre |
| Alternativ hypotese: | Den sande kumulerede fordeling er ikke en normal fordeling med de estimerede parametre |
| Kolmogorov-Smirnov Normality Test | Shapiro-Wilk Normality Test | |
| Bly | ks = 0.21, p-value = 0 | W = 0.64, p-value = 0 |
| PAH | ks = 0.24, p-value = 0 | W = 0.61, p-value = 0 |
| Kobber | ks = 0.11, p-value = 0.5 *** | W = 0.87, p-value = 0 |
| Zink | ks = 0.13, p-value = 0.024 | W = 0.93, p-value =0.0038 |
***Warning messages: The Dallal-Wilkinson approximation, used to calculate the p- value in testing composite normality, is most accurate for p-values <= 0.10 .The calculated p-value is 0.152 and so is set to 0.5, p-value is therefore not valid! Tabel A.3 Tests af normalfordeling
Som det ses af tabel A.3 kan ingen af de 4 variable tænkes at stamme fra en normalfordeling.
1.4 Loge transformerede data
Dernæst betragtes de logaritmerede (loge)værdier indledende med deskriptiv statistik, jf. tabel A.4.
| LnBly | LnPAH | LnKobber | LnZink | |
| Minimum | 3,14 | -5,99 | 2,104 | 4,01 |
| 1. Kvartil | 4,91 | -0,24 | 3,970 | 5,48 |
| Gennemsnit | 5,54 | 0,11 | 4,244 | 6,02 |
| Median | 5,87 | 0,58 | 4,388 | 6,21 |
| 3. kvartil | 6,25 | 1,08 | 4,691 | 6,72 |
| Max: | 7,89 | 3,08 | 5,720 | 7,22 |
| Antal | 50 | 50 | 50 | 50 |
| Nedre konfidensgrænse: | 5,24 | -0,45 | 4,050 | 5,77 |
| Øvre konfidensfrænse | 5,83 | 0,67 | 4,437 | 6,26 |
| Skewness | -0,76 | -1,46 | -0,921 | -0,62 |
| Kurtosis | 0,30 | 3,10 | 1,271 | -0,42 |
Tabel A.4 Deskriptiv statistik for de logaritmerede (loge)værdier
Det ses for alle 4 variable at middelværdi nu er mindre end medianen, samt at fordelingerne er lidt venstreskæve (venstre hale, skewness er negativ, kurtoisis relativ lille). Blandt ses at gennemsnittet(mean) angives til 254 med en konfidensinterval på 188 – 340 mg/kg TS mens for de ikke logaritme – transformerede data var gennemsnittet på 388 med en konfidensinterval på 274– 502 mg/kg TS. Medianværdier er selvfølgelig ens for begge datasæt og er på 355 mg/kg TS.
Korrelationen mellem de enkelte variable er vist i tabel A.5
| LnBly | LnPAH | LnKobber | LnZink | |
| LnBly | 1,00 | 0,70 | 0,78 | 0,81 |
| LnPAH | 0,70 | 1,00 | 0,65 | 0,79 |
| LnKobber | 0,78 | 0,65 | 1,00 | 0,79 |
| LnZink | 0,81 | 0,79 | 0,79 | 1,00 |
Tabel A.5 Korrelation for de logaritmerede (loge)værdier
Illustreret grafisk, der ses størst korrelation mellem Zink og Bly. Der ses at betydningen af de enkelte afvigende værdier (outliers) er "forsvundet". Dette er en af logaritmetransformationens fornemste opgaver.
Figur A.5 Korrelationsplot for de logaritmerede (loge)værdier
I figur A.6 vises de normalfordelings-fraktilplot for de logaritmetransformerede data.
Figur A.6 Normalfordelings-fraktilplotfor loge bly, PAH, kobber og zink
Der ses afvigelser fra normalfordelingen for alle 4 variable. Men nu er afvigelserne flyttet til venstre hale (negativ "skewness").
En anden måde at illustrere normalfordelings antagelserne er ved at plotte de kumulerede fordelinger for data og den tilhørende normalfordeling med parametrene middel og varians fra data, jf. figur A.7.
Figur A.7 Kumulerede fordelingsplot for de logaritmerede værdier
Dette afslører ligeledes afvigelser fra normalfordelingen, idet kurverne ikke er sammenfaldende. Afvigelserne er flyttet længere ned af den kumulerede fordeling qua transformationen.
Endelig kan det testes om de transformerede data kan tænkes at stamme fra en normalfordeling.
| Hypotese: | Den sande kumulerede fordeling er en normal fordeling med de estimerede parametre |
| Alternativ hypotese: | Den sande kumulerede fordeling er ikke en normal fordeling med de estimerede parametre |
| Kolmogorov-Smirnov Normality Test | Shapiro-Wilk Normality Test | |
| LnBly | ks =0.18, p-value=0.0002 | W=0.91, p-value=0.0012 |
| LnPAH | ks=0.2, p-value=0.0005 | W=0.88, p-value=0.0008 |
| LnKobber | ks=0.14, p-value=0.014 | W=0.93, p-value=0.0066 |
| LnZink | ks=0.11, p-value=0.5 *** | W=0.94, p-value=0.018 |
***Warning messages: The Dallal-Wilkinson approximation, used to calculate the p- value in testing composite normality, is most accurate for p-values <= 0.10 .The calculated p-value is 0.152 and so is set to 0.5. Tabel A.6 Tests af normalfordeling for de logaroritmerede værdier
1.5 Konklusion
- Hverken de originale data eller de transformerede data er normalfordelte.
- Logaritme transformationen er for "grov", idet fordelingerne skifter fra at være højreskæve til at være venstreskæve.
- Der ses enkelt outliers i de ikke-transformerede data, disse påvirker korrelation samt test for normalfordeling, disse bør dog ikke fjernes ved en "outlier" (afvigende værdier) undersøgelse idet det ofte er disse punkter der e r interessante.
- Til de fleste statistiske analyser vil de transformerede data være at foretrække for at mindske effekten fra ekstreme værdier.
Version 1.0 April 2004, © Miljøstyrelsen.