Diffus jordforurening og kulturlag
Bilag B
Teori ved geostatistik
1.1 Teori ved geostatistik
Den grundliggende ide i geostatistikken er at betragte værdier af geokemisk, geofysisk eller andre naturlige variabler som realisationer af en stokastisk proces i planen eller rummet /31/.
For enhver position, r, i et domæne, et plan eller et rum findes en målbar størrelse, z(r), en regionaliseret variabel, som er en realisation af en stokastisk variabel, Z(r). En regionaliseret variabel er en variabel, der gradvist ændrer egenskaber afhængig af positionen r.
Z(r) har en forventningsværdi, E{Z(r)}=μμ(r), og en auto-kovarians, Cov{Z(r), Z(r+h)}=C(r,h), hvor h er en forskydningsvektor. Hvis μμ(r) er konstant over hele det betragtede domæne, det vil sige μμ(r) = μ, siges Z at være første ordens stationær. Hvis autokovariansen kun afhænger af forskydningsvektoren, det vil sige, hvis C(r,h)=C(h), siges Z at være anden ordens stationær.
Ved anvendelse af kriging undersøges og modelleres den spatiale korrelation forud for estimationen af den målte parameter i alle andre punkter. Hertil anvendes semivariogrammet, der formelt kan udtrykkes ved:
γ (r,h)=E{[Z(r+h)-Z(r)]2}/2
Det gælder også, at semivariogrammet kun afhænger af forskydningsvektoren, hvis Z er anden ordens stationær.
I praksis anvendes det eksperimentelle semivariogram, der er en diskretisering af det formelle semivariogram, hvor semivariansen estimeres i diskrete afstandsintervaller, som det halve af de kvadrerede differencer mellem prøvepunkterne. Hvis semivariogrammet er uafhængig af retningen af forskydningen, siges Z at være isotropisk. Hvis det omvendt er afhængigt af retningen, siges Z at være anisotropisk. De enkelte diskrete afstandsintervaller i diskretiseringen betegnes lags.
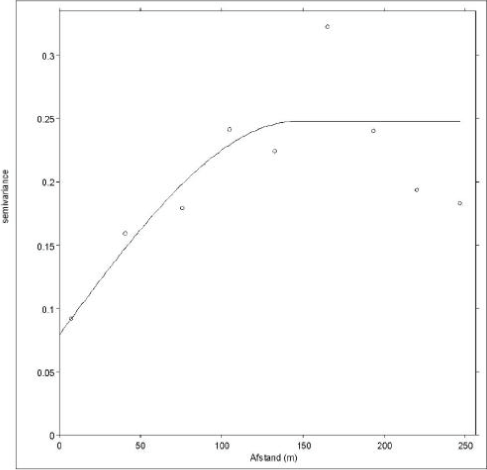
Figur b.1 Semivariogram for blykoncentrationer målt på testareal D - Banefløjen.
Semivariogram for lead concentrations for test area D - Banefløjen
I figur B.1 er vist et eksempel på et semivariogram, der viser variansen i blykoncentrationer målt på testareal D - Banefløjen (jf. kapitel 6). Semivariogrammet viser, at semivariansen vokser med lagafstanden, og dermed at målingerne er spatialt korrelerede. Kurven angiver den modellerede spatiale korrelation eller variogrammodel, der er tilpasset ved hjælp af mindste kvadraters metode til en generel sfærisk model. Til estimationen af variogrammodellen er anvendt den geostatistiske applikation "gstat" /30/ til statistikprogrammet R.
Den generelle sfæriske variogrammodel er givet ved:
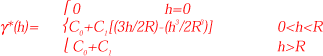
Den afstand, hvor modellen er konvergeret mod det gennemsnitlige maksimale niveau for semivariansen R, betegnes range.
Denne er ikke i alle modeller noget klart defineret punkt, og er ikke med sikkerhed nået inden for den undersøgte afstand i ovenstående figur. Modellen i figuren beskriver, at der selv imellem punkter, der har en meget meget lille indbyrdes afstand, er en ikke ubetydelig varians, svarende til C0 i den matematiske modelformulering. Denne betegnes "nugget", og er her et udtryk for summen af jordmediets mikrovariation og måle-/analyseusikkerhed, der vil bidrage til usikkerheden på estimatet af blykoncentrationen i ethvert punkt, uanset afstanden til nært beliggende målepunkter. Endelig betegnes den maksimale varians C0+C1 for "sill "og som er lig med den samlede varians i det undersøgte domæne for den betragtede variabel.
Variogrammodellen kan anvendes til at fastlægge vægtningen af de målte punkter i estimationen af værdierne i alle øvrige punkter ved hjælp af kriging. De fleste metoder, herunder simpel, ordinær og universal kriging bygger på en gaussisk eller normalfordelt stokastisk variabel. Det er attraktivt, at metoderne foruden at give et estimat for Z(r) for et vilkårligt punkt r, også gør det muligt at estimere variansen for dette. Da Z(r) er normalfordelt, kan variansen direkte anvendes til at beregne et approksimativt konfidensinterval for den estimerede værdi.
Alle tre metoder forudsætter, at variogrammet er uafhængigt af stedvektoren og kun afhænger af forskydningsvektoren. Det kan vises, at dette gælder, såfremt Z(r) er anden ordens stationær. Det omvendte er imidlertid ikke altid tilfældet /30/. Endvidere forudsættes i simpel kriging, at Z(r) er første ordens stationær. Det vil sige, at den estimerede værdi er kendt og uafhængig af stedvektoren. I praksis vil simpel kriging derfor ofte virke udglattende på de forskelle, der tegner sig inden for et geografisk område. Ved ordinær kriging er dette løst ved at estimere Z(r) på grundlag af punkter indenfor et mindre naboområde. I denne model opfattes Z(r) som en regionaliseret stokastisk variabel med en kontinuerligt varierende estimeret værdi. I universal kriging er den estimerede værdi en funktion af fysiske parametre, der forårsager en trend i den estimerede værdi. Dette kunne i relation til diffus jordforurening eksempelvis være retning og afstand fra en kendt punktkilde.
Version 1.0 April 2004, © Miljøstyrelsen.