Erfaringsopsamling på udviklingen i poreluftkoncentrationer på villatanksager
Bilag C: Fraktilestimater
For at få en struktureret og kvantitativ databearbejdning, er der for hver dataanalyse i rapportens afsnit 2, optegnet estimerede tidslige fraktilplots for de scatterdata, der er præsenteret i de viste plots:
Plot A: Koncentration som funktion af tid efter spildtidspunkt/afværgeafslutning.
Plot B: Normeret koncentration (C/Cmax) som funktion af tid efter spildtidspunkt/afværgeafslutning.
I det følgende er den statistiske procedure, der ligger til grund for estimering af henholdsvis 50, 75 og 90 % fraktiler for de indsamlede poreluftdata, beskrevet – via et eksempel baseret på TVOC-data fra alle poreluftmålepunkter under ét (jf. afsnit 2.3.1).
Scatterdata for TVOC – plot A for alle data – er således vist i figur C.1. Som det fremgår af figur C.1 er der meget stor forskel på datatætheden til forskellige tidspunkter, således at datatætheden er betydeligt højere i starten end i slutningen af tidsaksen. Samtidig observeres nogle visuelle tendenser for de øvre niveauer i datasværmen, som (på øjemål) er indtegnet med blå linjer i plottet. ”Problemet” er at de indtegnede blå linjer afhænger af øjnene der ser, og primært repræsenterer de ekstreme værdier i datamaterialet. Endvidere, hvordan afvejes de to tendenser? Og hvad er middeltendensen?
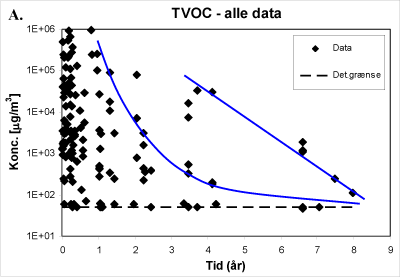
Figur C.1. Scatterplot for TVOC – alle poreluftmålepunkter.
For at undgå subjektivitet i datatolkningen er der opstillet en standardiseret metodik til fraktilestimering, som er ”programmeret” i Excel og som beskrives i det følgende.
Havde data været målt på ”pæne/ordnede” tidspunkter; f.eks. efter 0,25, 0,5 og 1 år osv. ville man til hvert tidspunkt kunne estimere fraktiler ved en simpel rangordning af koncentrationsdataene til hvert tidspunkt. Var der f.eks. 10 datapunkter målt til tiden 1 år efter spildtidspunkt/afværgeafslutning, ville 90 % fraktilet eksempelvis kunne estimeres som den næsthøjeste koncentration der var målt (90 % af de målte data til tiden 1 år er mindre end eller lig den målte værdi). Tilsvarende ville 75 % fraktilet kunne estimeres som middelværdien af den 7. og 8. laveste værdi, og så fremdeles.
Nu er data imidlertid ikke målt på ordnede tidspunkter, hvorfor der er foretaget en tidsmæssig gruppering af de målte data, således, at det indenfor hver tidsmæssig gruppering er muligt, at estimere fraktiler, som om data indenfor hver gruppering var målt til samme tidspunkt. Dette er essentielt en form for numerisk statistik.
Hver gruppering er som udgangspunkt valgt således, at der er mindst 10 datapunkter repræsenteret i hver gruppe – hvilket dog ikke er muligt i ”tynde” områder af plottet; f.eks. efter 6,5 år i figur C.1, eller for dataanalyser med få data i datagrundlaget. Desuden er grænserne forsøgt valgt således at de (efterfølgende) estimerede fraktiler ikke misrepræsenterer data i scatterplottet. For data i figur C.1 kommer gruppeinddelingen til at se ud som i figur C.2.
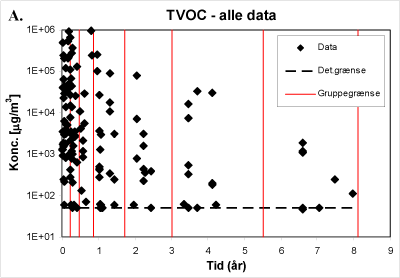
Figur C.2. Gruppeinddelinger af data, til estimering af fraktiler indenfor hver gruppe.
Efterfølgende er fraktilfunktionen i Excel benyttet til at estimere hhv. 50, 75 og 90 % fraktiler for hver gruppe. Fraktilestimaterne for hver gruppe er efterfølgende tilegnet den tidslige middelværdi i hver gruppe – og der er optegnet linjer imellem estimaterne for hver datagruppering.
Fraktilfunktionen i Excel benytter et estimat, der er baseret på følgende formel for den empiriske fordelingsfunktion (frem for at den 9. laveste værdi repræsenterer 90 % fraktilen) /5/. Efter denne formel fordeles ”halerne” af fordelingen udenfor både den lave og høje ende af datapunkterne, frem for kun udenfor den lave ende, hvilket giver nogle mere intuitive fraktilestimater.
![]()
Hvor i er nummeret på observationen, efter rangordning, N er antallet af observationer i den enkelte gruppering og Fn(X) er den empiriske fordelingsfunktion; dvs. den fraktion af data der er mindre end eller lig med værdien for observation nr. i.
Fraktilestimaterne i ovenstående eksempel bliver som vist i figur C.3, hvor estimaterne for hver gruppe er markeret som en tom cirkel, og hvor den tidsmæssige placering af gruppeestimatet altså repræsenterer den tidlige middelværdi for punkterne i hver gruppe.
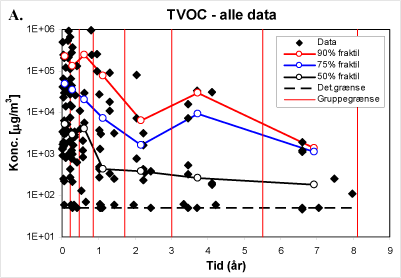
Figur C.3. Fraktilestimater (50, 75 og 90 %) for hver gruppeinddeling.
Slutteligt er der foretaget en afkortning af fraktilestimaterne, i den endelige visuelle fremstilling af fraktilplottene, således at linjerne tilhørende hvert fraktilestimat stoppes til det tidspunkt, hvor datamaterialet ”slipper op” i forhold til at give meningsfyldte estimater.
Som forudsætning for at optegne 50 % fraktilet, er det således sat, at der skal være minimum to datapunkter i det tidsinterval, som fraktilet er beregnet på baggrund af. Dvs. at 50 % fraktilet repræsenterer den koncentration, som halvdelen af data (mindst ét datapunkt) er lavere end. Tilsvarende er det forudsat, at der skal være mindst 4 datapunkter for beregning og plotning af 75 % fraktilet, svarende til den koncentration, som ¾ af datapunkterne (minimum tre) ligger under, og at der skal foreligge mindst 10 datapunkter for beregning af 90 % fraktilet (værdien for mindst ni datapunkter er lavere).
Det endelige resultat er vist i figur C.4.
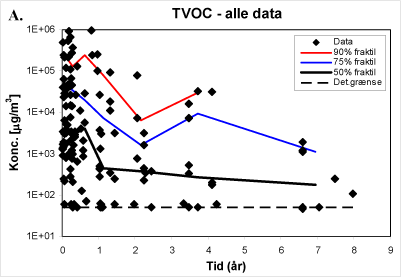
Figur C.4. Endelig præsentation af fraktilestimater (50, 75 og 90 %) for TVOC – alle data.
Som det fremgår af plottet, ”fanger” metoden tendenserne i datamaterialet, og der foretages en afvejning af de to tendenser der rent visuelt kunne observeres i det oprindelige scatterplot (figur C.1). Ydermere giver plottet mulighed for en kvantitativ tolkning, af såvel middeltendensen for datamaterialet (50 % fraktilet) som de mere ekstreme tendenser; hhv. via 75 og 90 % fraktilerne.
Version 1.0 December 2009, © Miljøstyrelsen.