1 Dimensioneringsprogrammets forudsætninger

Dimensioneringsværktøj for brændeovne - Web baseret simuleringsværktøj for bestemmelse af den korrekte brændeovnsstørrelse til den specifikke bolig.

1.1 Rummets varmebalance

For opholdszonen i en bolig er temperaturen den altdominerende indeklimafaktor. Enhver som træder ind i et rum, vil ud over de optiske indtryk først og fremmest registre temperaturen. Opvarmningssystemet og herunder brændeovnen bør derfor være således indrettet, at der hele året (dog specielt om vinteren) kan holdes en behagelig rumtemperatur. Rummets varmebalance må være i orden. Varmebalancen påvirkes imidlertid af mange faktorer:

Varmetransmission, ind eller ud, gennem rummets yderflader
Ventilationsluftens temperatur og mængde
Brændeovnens varmeafgivelse
Personernes varmeafgivelse
Belysningsvarme
Elektriske maskiners varmeafgivelse
Solindfald gennem vinduer og andre yderflader
Varmeakkumulering i bygningsdele og inventar
Tidspunktet og tiden for benyttelsen af rummet.

Varmebalanceligningerne beskriver samspillet mellem disse faktorer, og de udtrykker blot, at den tilførte varme er lig summen af varmetabet og den akkumulerede varme. Men da forholdene ikke er stationære, bliver ligningerne komplicerede og lader sig ikke umiddelbart løse.

I det følgende er vist, hvorledes temperaturforholdene i et rum kan beregnes for ikke stationære forhold. Den nedenfor beskrevne metode er i det væsentlige baseret på Bo Adamsons arbejde /Bo Adamson, Värmebalans vid rum och byggnader, Tekniska Högskolan i Lund, 1968/. Der er dog ændret en smule på beregningsmodellen, og beregningsudtrykkene er udformet som differensligninger. Dette bevirker en lettelse i beregningsgangen og en væsentlig udvidelse af anvendelsesområdet. Beregningsmetoden er i almindelighed tilstrækkelig nøjagtig, den er let og overskuelig, og kan klares med fx Excel regneark eller lignende værktøjer. Beregningsmetoden har været brugt gennem årene i programmerne TEMPFO4, /Bo Andersen Indeklimatemperatur og energiforbrug i bygninger beregnet ved referenceårets vejrdata, SBI – rapport 93, Statens Bygningsinstitut, Hørsholm 1974/. Tsbi1, /Termisk simulering af bygninger og installationer, version 2.1, Statens Byggeforskningsinstitut 1985/ samt Tsbi2 og Tsbi3 (nyere versioner af simuleringsprogrammet).

Figur 1: Temperaturforløb ved pludselig ændring af rummets varmebelastning

Figur 1: Temperaturforløb ved pludselig ændring af rummets varmebelastning

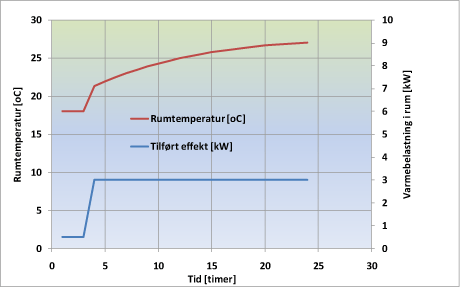
På figur 1 er vist en forenklet fremstilling af temperaturforløbet i et rum, hvor varmebelastningen pludselig ændres, efter at den i lang tid har været konstant, f.eks. ved optænding i brændeovn.

Det første stykke tid vil temperaturændringen pr. tidsenhed være forholdsvis stor, og overfladetemperaturen vil stige sammen med lufttemperaturen. Efterhånden som temperaturen stiger, vil også varmetabet stige, og temperaturstigningen vil blive langsommere. Den endelige temperatur nås først efter meget lang tid.

Et tilsvarende udtryk for temperaturforløbet findes som følger: Rummets varmeudveksling med omgivelserne pr. ^oC temperaturdifferens sættes til B [W/^oC], varmebelastningen til Q [W], og varmekapaciteten for rummet til S [W/^oC], hvilket giver:

hvor t er rumtemperaturen [^oC]
t_u er udetemperaturen [^oC]
τ er tiden [h].

Efter integrering af denne ligning og passende omskrivninger fås:

hvor tidskonstanten er

Den afgørende termiske komfortfaktor er rumtemperaturen, der er et konglomerat af indelufttemperaturen t_i og de indvendige overfladetemperaturer t_o, og det er altså disse to temperaturer, der må beregnes til forskellige tidspunkter.

Den betragtede tid opdeles i intervaller Δτ, og til hvert tidspunkt eller interval opstilles tre varmebalanceligninger for:

rumluften
overfladerne
de varmeakkumulerede dele

med de tre ubekendte temperaturer for:

indeluften, t _i[^oC]
overfladerne, t _o[^oC]
de varmeakkumulerende dele, t_a[^oC].

For at komme gennem beregningerne tænkes de varmeakkumulerende dele koncentreret i uendelige tynde lag i de respektive vægge, gulv og loft, og de tre nævnte temperaturer antages hver for sig at være den samme overalt. Herved bliver det muligt at forenkle ligningerne så meget, at de kan løses, og der kan opstilles et udtryk for hver af de tre temperaturer.

1.2 Beskrivelse af model – varmebalancerne

Hvis beregningerne skal være meget nøjagtige, må der opstilles et meget stort antal ligninger, principielt én for hver temperatur af overfladerne og tynde lag af de varmeakkumulerende dele, der ønskes. Som nævnt er det dog i mange tilfælde tvivlsomt, om dette besvær lønner sig. Her er derfor søgt realistisk forenkling med kun tre ligninger for hvert tidsinterval.

1.2.1 Rumluftens varmebalance

Rumluften tilføres varme ved konvektion fra en del af varmen, der afgives af personer, belysning, maskiner, brændeovn m.m., og det samlede bidrag benævnes Q_k [W]. Endvidere sker der en varmeoverføring pr. grad temperaturforskel til eller fra rummets overflader ligeledes ved konvektion, der benævnes B_o [W/^oC], og som er bestemt af overfladearealerne og de konvektive varmeovergangstal ved:

hvor α er det konvektive varmeovergangstal for lodrette flader 3,3 W/(m² ^oC) og 2,3 W/(m² ^oC) for vandrette flader

A er overfladearealet [m²]
t_o er overfladernes temperatur [^oC]
t_i er rumlufttemperaturen [^oC].

Fra rumluften bortledes eller tilføres varme ved ventilationsluften pr. ^oC temperaturdifferens B_l [W/^oC] eller i alt:

hvor G er ventilationsluftmængden, naturlig eller mekanisk [kg/h]

c er luftens varmekapacitet [J/(kg ^oC)]
t_l er indblæsningsluftens temperatur [^oC].

Idet der ses bort fra den helt ubetydelige varmeakkumulering i rumluften, bliver varmebalanceligningen for rumluften:

ligning (1)

1.2.2 Overfladernes varmebalance

Den samlede mængde strålevarme der tilføres overfladerne, benævnes Q_s [W]. Ved transmission gennem væggene bortledes varme til det fri og måske til omgivende rum.

Varmeoverføringen fra overfladerne til den anden side benævnes:

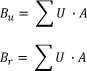
Formel

hvor B_u er til ’det fri’, og B_r er til ’omgivende rum’ [W/^oC].

Transmissionstallene beregnes på sædvanlig måde efter Dansk Ingeniør Forenings regler for beregning af varmetab. Ydervæggene og vinduernes indvendige overfladetemperatur vil ligge lavere end den gennemsnitlige overfladetemperatur t_o, og dette tages der i nogen grad hensyn til ved at medregne den indvendige overgangsmodstand i transmissionsmodstanden. Ved indervæggene medregnes også den indvendige overgangsmodstand, idet indervæggene for en stor del vil være dækkede af møbler, billeder, tekstiler mv.

Fra overfladerne afgives endvidere varme til rumluften som beskrevet i forrige afsnit. Desuden afgives varme fra overfladerne til de varmeakkumulerende dele i væggen. For at forenkle beregningerne tænkes de varmeakkumulerende dele samlet i et uendeligt tyndt lag med passende placering i det indre af væggen, gulvet eller loftet med samme temperatur t_a overalt.

Varmeoverføringen fra overfladerne til de varmeakkumulerende lag benævnes:

hvor U_a er transmissionstallet fra overfladen til det varmeakkumulerende lag [W/^oC].

Varmebalanceligningen for overfladerne bliver herefter:

ligning (2)

1.2.3 De akkumulerende lags varmebalance

Fra overfladerne ledes varme ind i væggene, hvor den akkumuleres. Denne varmestrøm vil ikke være konstant, da overfladetemperaturen varierer over døgnet. For at forenkle beregningerne tænkes som nævnt væggens varmekapacitet samlet i et uendeligt tyndt lag med samme temperatur t_a for alle de seks fiktive varmeakkumulerende lag, der omgiver rummet. Dette er naturligvis en stærk forenkling, og det fiktive lag må også placeres med omtanke. Det skulle gerne være således, at tidskonstanten, forholdet mellem varmekapaciteten og varmestrømmen, er af samme størrelsesorden for alle vægdele; i modsat fald må der korrigeres. Fordelen ved denne forenkling er brugen af kun én differentialligning.

Afhængig af temperaturfaldets retning vil væggen akkumulere eller afgive varme. Idet temperaturen ændrer ∂t_a i løbet af tiden ∂τ, bliver den akkumulerende varmemængde pr. tidsenhed:

hvor S er rummets varmekapacitet [J/^oC]

c_p er byggematerialernes varmekapacitet [J/(kg ^oC)]
ρ er massefylden [kg/m³]
A er arealet [m²]
t er tykkelsen [m].

Varmebalanceligningen for det varmeakkumulerende lag bliver hermed:

ligning (3)

Ligning (3) må ændres til en differensligning for at kunne behandles på pc.

1.2.4 Det samlede ligningssystem

Det samlede ligningssystem får herefter følgende udseende:

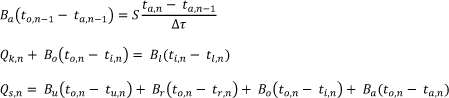
Formel

Nedenfor er vist et eksempel på afvikling af ligningssystemet på et ventileret rum med sol- og personbelastning. Starttemperaturen er overalt sat til 20 °C.

Figur 2: Eksempel på temperaturberegning

Figur 2: Eksempel på temperaturberegning

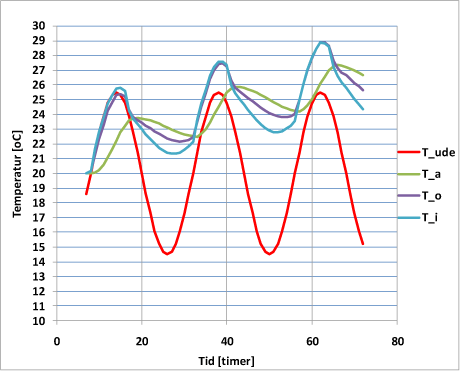
Diagrammet viser et eksempel på beregnet temperaturforløb i rum. X-aksen er timer, Y-aksen er °C, Tu er udetemperaturen, Ta er temperaturen i det akkumulerende lag i væggene, To er overfladetemperaturen på væggene, og Ti er lufttemperaturen i rummet.