12 Appendiks

Udvikling af en metode til effektvurdering af Miljøstyrelsens Kemikalieinspektions tilsyn og kontrol

12.1 Materiale modtaget fra MST

Smykkekortlægning:

http://www2.mst.dk/common/Udgivramme/Frame.asp?
http://www2.mst.dk/Udgiv/publikationer/2008/978-87-7052-773-6/html/default.htm

Negleprojekt:

http://www.mst.dk/Udgivelser/Publikationer/2008/07/978-87-7052-786-6.htm

Projektbeskrivelse for et tilsynsprojekt:

Modtaget i Word

Designguide, logo og retningslinjer for opbygningen af udgivelser og projektartikler fra MST:

http://www.mst.dk/Kontakt/Specielt+for+leverandører/Designprogam/

Årsberetninger:

http://www.mst.dk/Kemikalier/Kontrol+og+tilsyn/Aarsberetninger/

Tidsforbrug pr. produkt:

Modtaget i Word

Manual til kortlægning af producenter, importører og forhandlere:

http://www2.mst.dk/common/Udgivramme/Frame.asp?http://www2.mst.dk/ udgiv/publikationer/2008/978-87-7052-800-9/html/default.htm

RoHS substances (Hg, Pb, Cr(VI), Cd, PBB and PBDE) in electrical and electronic equipment in Belgium:

Modtaget i pdf

12.2 Kontaktpersoner i MST

PwC har haft kontakt med følgende personer i MST:

Flemming Hovgaard Jørgensen
Birte Børglum
Dorrit Skals.

12.3 Udledning af fejlleddet

En tommelfingerregel for (maksimal eller ”konservativ”) andelen B kan udledes af, at estimatet for en andel, (hvor X er antallet af ”succes”-observationer) er en binomial fordeling, som har en maksimal varians på 0,25 for parameter ρ = 0,5). Så stikprøven X/n har højst en varians på 0,25/n. For tilstrækkeligt store n vil fordelingen kunne estimeres ved en normalfordeling med det samme gennemsnit og varians.

Denne tilnærmelse kan bruges til at påvise, at 95 % af denne fordelings sandsynlighed ligger inden for to standardafvigelser af gennemsnittet. Derfor vil et interval af formen:

danne et 95 procents konfidensinterval omkring den sande andel.

Hvis vi kræver, at fejlleddet ε ikke overstiger grænsen B, kan vi løse ligningen:

som giver os

12.4 Stikprøvestørrelser for hypotesetest

Et almindeligt problem for statistikere er beregning af stikprøvestørrelsen krævet til at give en vis præcision til en stikprøve, givet en forudbestemt Type I-error α (fejlmargin). Et typisk eksempel for dette følger:

Lad x_i, i = 1, 2, ..., n være uafhængige observationer fra en normalfordeling med middelværdi µ og varians σ². Lad os betragte to hypoteser, en nul-hypotese:

H₀: µ = 0

og en alternativ hypotese:

H_alt: µ = µ^*

for en ”mindste signifikante forskel” µ^* > 0. Dette er den mindste værdi, som vi interesserer os for i forbindelse med at iagttage en forskel.

Hvis vi ønsker at (1) forkaste H₀ med en sandsynlighed på mindst 1-β, når H_alt er korrekt (dvs. en styrke på 1- β), og (2) afvise H₀ med sandsynlighed α, når H_alt er sand, så får vi brug for følgende:

Hvis z_α er den øvre α -procentpoint-værdi af standard-normalfordelingen (middelværdi 0 og varians 1), så gælder det at:

og udsagnet ”forkast H₀, hvis vores stikprøvegennemsnit α er større end ”, er en beslutningsregel, der opfylder (2). (Bemærk, at der her er tale om en ensidet test).

Nu ønsker vi, at dette kan ske med en sandsynlighed på mindst 1- β, når H_alt er sand. I dette tilfælde vil vores stikprøvegennemsnit komme fra en normalfordeling med middelværdi µ^*. På den baggrund vil vi kræve, at:

Ved omskrivning kan det vises at være opfyldt, når

hvor Φ er normalfordelingens fordelingsfunktion.

12.5 Udledning af den statistiske model

I det følgende beskrives udledningen af den statistiske model til beskrivelse af det samlede antal ulovlige produkter på markedet.

I tabellen nedenfor er de væsentligste statistiske egenskaber ved normalfordelingen og binomialfordelingen anført:


Fordeling	Middelværdi	Varians	Standardafvigelse
Bin(n,ρ)	n · ρ	nρ(1-ρ)
N (µ, σ²)	µ	σ²	σ

Antal produkter i populationen, N

Det samlede antal produkter i populationen, , antages at være normalfordelt med parametre µ og σ, dvs. formelt:

De statistiske egenskaber ved fordelingen for er ligetil:

Frekvensen af ulovlige produkter i populationen, ρ

Frekvensen af ulovlige produkter i populationen, ρ, estimeres på baggrund af en stikprøve givet ved:

Antallet af observationer, n og antallet af fundne ulovlige produkter, u.

ML-estimatet for ρ er dermed givet ved (idet vi ser usom realisationen af en binomialfordelt stokastisk variabel):

ML-estimatoren også er binomialfordelt, man siger, at . Variansen af estimatoren er derfor givet ved ρ² = ρ(1- ρ)/n, og standardafvigelsen er dermed givet ved ρ.

Ulovlige produkter i populationen, U

Antag, at antallet af ulovlige produkter i populationen er binomialfordelt med antalsparameter og sandsynlighedsparameter ρ, dvs. .

De statistiske egenskaber (middelværdi, varians og standardafvigelse) ved fordelingen for er givet ved:

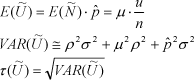
Formel

I beregningen af variansen udnyttes approksimationen, at for tilpas store n gælder det, at binomialfordelingen med parametre (n,ρ) ”ligner” normalfordelingen med parametre (nρ, nρ(1 - ρ)), og derefter anvendes formlen for varians af produktet af to normalfordelte variable..