Statistisk analyse og biologisk tolkning af toksicitetsdata
2 Dosis-responsmodeller
Der er en lang række parametriske modeller tilgængelige til at beskrive dosis-responsdata. I dette afsnit introduceres de mest almindeligt anvendt parametriske dosis-responsmodeller inden for toksikologien. Disse modeller har ofte et s-formet (sigmoidt) kurveforløb, men det skal nævnes at der også findes andre modeller så som log-dosis lineære, eksponentielle og ikke-monotone dosis-responsmodeller.
Det er fælles for mange af de inkluderede dosis-responsmodeller, at modelparametrene har en biologisk fortolkning. I Figur 2.1 kan man se en grafisk fremstilling af en karakteristisk dosis-respons kurve, hvor responsen nærmer sig en øvre grænse, når doseringen nærmer sig 0 (ubehandlet kontrol, dvs. dosis 0), og en nedre grænse, når doseringen bliver stor (f.eks. gående mod en fuldstændig hæmning ved høje doseringer). Den øvre og nedre grænse betegnes ofte som asymptoter. Den dosering eller koncentration, der fremkalder en virkning midt imellem de to asymptoter, er den dosering/koncentration, som giver en effekt på 50% i forhold til de øvre og nedre grænser. Denne dosering betegnes ofte ED50/EC50, hvor ”E” refererer til en målt effekt og ”D” hhv. ”C” refererer til dosis hhv. koncentration. Figur 2.1 er et eksempel på data opnået i en test med kontinuert respons (f.eks. vækstratehæmning), men tilsvarende overvejelser gælder for diskret respons (f.eks. test med responset død/levende), hvor pedanten til ED50/EC50 ofte betegnes LD50/LC50 (”L” står for lethal altså dødelig). Til kvantificering og klassificering af et kemikalies effekt opsummeres de toksikologiske data ofte vha. 50%’s værdierne (LC50/LD50/EC50/ED50), men inden for human- og økotoksikologien kan der også være andre responsniveauer man er interesseret i, f.eks. effekter i det lave område, hvor det ofte er 10%’s værdierne, der anvedes (LC10/LD10/EC10/ED10). Disse er også vist i Figur 2.1.
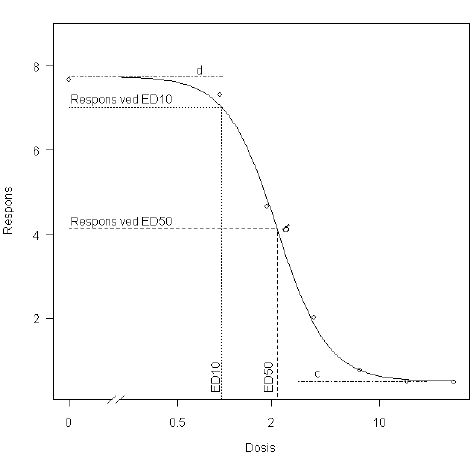
Figur 2.1. Illustration af en log-logistisk dosis-responskurve, hvor den øvre (d) og den nedre (c) grænse er vist. Hældningen på kurven svarende til doseringen ED50 er angivet ved parameteren b (se model 2.1).
De sigmoide dosis-responsmodeller omfatter to typer, som ofte anvendes til at beskrive henholdsvis symmetriske og asymmetriske kurveforløb for monotont faldende eller stigende dosis-responsdata:
1) Den log-logistiske model vist i Figur 2.2 og ligning 2.1
2) De to Weibull-modeller vist Figur 2.3 og ligning 2.2. og 2.3
Som et særligt vigtigt eksempel skal den log-logistiske fire-parameter model nævnes. Den er defineret ved ligningen
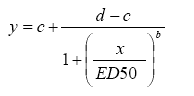 (2.1)
(2.1)
De fire parametre i Ligning (2.1) betegnes henholdsvis b, c, d, og ED50. Parameteren ED50 betegner, som tidligere nævnt, den dosering, der resulterer i en respons midt mellem den nedre grænse c og den øvre grænse d. Parameteren b er proportional med hældningen på kurven omkring ED50 (Streibig et al, 1993). Parametrene er vist på Figur 2.1. Ligning (2.1) er monotont faldende, hvis parameteren b er positiv, og stigende, hvis b er negativ.
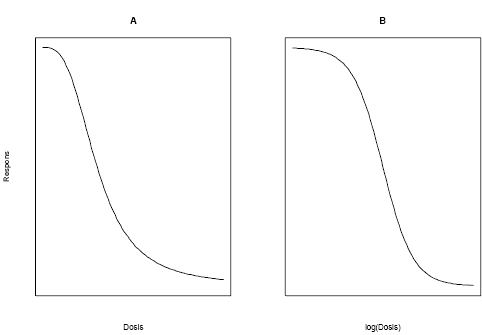
Figur 2.2. Den log-logistiske dosis-responskurve som funktion af dosis (A) og logaritme-transformeret dosis (B).
Som det fremgår af Figur 2.2 er kurven asymmetrisk, når man benytter en dosis-akse, der ikke er logaritmeret. Ligning (2.1) kan omskrives til Ligning (2.1a), som benytter log(x) i stedet for x
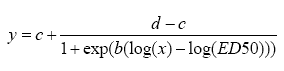 (2.1a)
(2.1a)
Matematisk er Ligning (2.1) og (2.1a) identiske, men det er oftest formuleringen i ligning (2.1a), der benyttes i publikationer. Det er ofte muligt at antage, at den nedre grænse er 0, og den tilsvarende log-logistiske tre-parametermodel fås ved at sætte c=0 i Ligning (2.1) og (2.1a). Den resulterende ligning er vist i Ligning (2.1b).
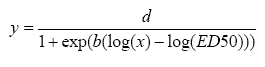 (2.1b)
(2.1b)
De to Weibull-modeller er den anden hovedtype af modeller, der betragtes i dette projekt (Seber and Wild 1989, s. 338–339). De er kendetegnet ved at være asymmetriske, og Figur 2.3 illustrerer forskellene i kurveforløbene for de to Weilbull-modeller. Den ene model har et kurveforløb, som er langsomt aftagende fra den øvre grænse (Figur 2.3 til venstre), mens den anden model har et forløb, som aftager hurtigt fra den øvre grænse (Figur 2.3 til højre).
Figur 2.3. De to Weibull-modeller er begge asymmetriske. Weibull-1-modellen er langsomt aftagende fra den øvre grænse, mens Weibull 2 er hurtigt aftagende fra den øvre grænse.
Begge Weibull-modeller har også fire parametre. Weibull-1-modellen er defineret ved ligningen
![]() (2.2)
(2.2)
Weibull-2-modellen er givet ved ligningen
![]() (2.3)
(2.3)
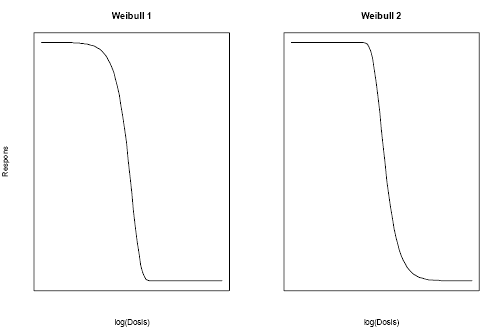
Parametrene c og d svarer til den nedre og øvre grænse ligesom for den log-logistiske model (Ligning (2.1)). Parameteren e svarer til den dosering, hvor dosis-responskurven har en vendetangent, men pga. det asymmetriske kurveforløb svarer denne dosering ikke til ED50. Parameteren b er proportional med hældningen på kurven omkring e. For begge Weibull-modeller vil en fastsat nedre grænse på nul (c=0) reducere de fire parametre til tre parametre på samme måde som for den logistiske model (Ligning 2.1b). ED50 er som sagt ikke en parameter, der direkte indgår i Ligning (2.2) eller Ligning (2.3). Man kan dog stadig udregne ED50 på grundlag af parametrene i modellen.
I visse situationer er et observeret dosis-responsforløb ikke-monotont som funktion af dosis, f.eks. kan der ske en hæmning eller en stimulering af responsen ved meget små doseringer som vist i Figur 2.4. Dette benævnes hormesis (Cedergreen et al, 2005). Denne type dosis-responsforløb kan beskrives ved en model afledt af den log-logistiske model i Ligning (2.1a) med følgende ligning
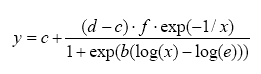 (2.4)
(2.4)
Ligning (2.4) giver anledning til en model med fem parametre, hvoraf kun d og c har samme fortolkning som i den log-logistiske model. Modellen kan benyttes til at beskrive data, der udviser hormesis. Parametren f i Ligning (2.4) beskriver den maksimale størrelse på den hormesis effekt (Cedergreen et al, 2005).
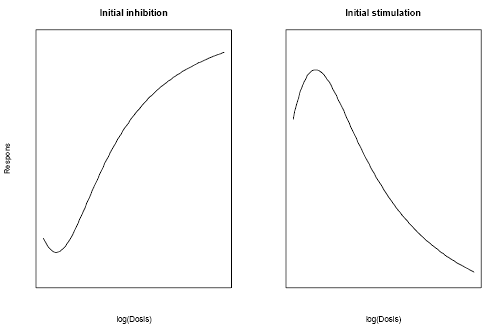
Figur 2.4. Hæmning eller stimulering ved lave doseringer, som kan beskrives med forskellige modeller, der er afledt af den log-logistiske model i Ligning (2.1a). Ved initiale hæmning er parameteren b i Ligning (2.4) og (2.5) negativ, mens parameteren b for en initial stimulering er positiv.
I visse tilfælde kan en yderligere modifikation af Ligning (2.4) give en bedre beskrivelse af data med hormesis. Den modificerede model har følgende ligning
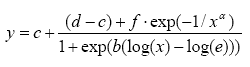 (2.5)
(2.5)
Ligning (2.4) svarer til at sætte α=1 i Ligning (2.5). Modellen baseret på Ligning (2.5) involverer seks parametre, hvor den sjette parameter er α (Cedergreen et al, 2005). Hvis data ikke tillader en bestemmelse af α, kan den fastsættes a priori, f.eks. som i Ligning (2.4). Andre er a priori valg af α til at være 0,25 eller 0,5. Hvis der derimod er tegn på hormesis, det endvidere er muligt at tilpasse modellen baseret på Ligning (2.5), så kan man efterfølgende teste hypotesen α =1 vha. et formelt statistisk test. Det er igen muligt at udregne ED50 ud fra modelparametrene under den antagelse, at niveauet til dosis 0 tages som den øvre grænse, hvilket i dette tilfælde ikke svarer til det størst mulige responsniveau. Praktiske erfaringer viser, at den maksimale respons i datasæt med hormesis ofte viser større variation end respons til dosis 0 (Cedergreen et al, 2005).
I Tabel 2.1 er der en forklaring på de parametre, som indgår i de ovennævnte ligninger.
Tabel 2.1. Oversigt over biologisk fortolkning af parametrene i Ligning (2.1)-(2.5). Hormesis hentyder i denne sammenhæng til de ikke-monotone modeller i Ligning (2.4) og (2.5).
| matematiske udtryk | modeller | |||
| log-logistisk | weibull 1 | weibull 2 | hormesis | |
| øvre grænse | d | d | d | d |
| nedre grænse | c | c | c | c |
| ec50 | ed50 | udledes fra ligning | udledes af ligning | udledes af ligning |
| monoton | ja | ja | ja | nej |
| symmetrisk | ja, på log-dosis akse | nej | nej | nej |
Ved at benytte de parametriske modeller, som vi har beskrevet ovenfor, opnår man den fordel, at man kan teste forskellige biologiske hypoteser. For eksempel kan man vha. statistiske metoder teste om man kan tillade sig at antage identiske parametre for dosis-responskurver. Imidlertid er forudsætningen for at benytte disse modeller, at der findes en funktionel sammenhæng. Fra et teoretisk synspunkt passer et sigmoidt kurveforløb ind i vores forestillinger om, hvorledes f.eks. en receptor vil reagere på en stigende dosis/koncentration af et kemikalie. Imidlertid vil der i mindre kontrollerede miljøer være tilfælde, hvor der ikke er så klare funktionelle sammenhænge mellem dosis og respons. I de tilfælde kan man forsøger sig med at benytte ikke-parametriske eller semi-parametriske metoder, som helt eller delvist giver slip på en underliggende parametrisk model for det overordnede kurveforløb. Dette emne berøres kort senere i rapporten.
Sammenligning af dosis-responskurver
Som vist i Figur 2.5 er der i princippet to forskellige måder, hvorpå man kan sammenligne to dosis-responskurver: en vertikal sammenligning (som vist i Figur 2.5A) og en horisontal sammenligning (som vist i Figur 2.5B) (Streibig, 1988). Dosis-responskurverne kunne f.eks. vise to pesticiders virkning på en testorganisme, afprøvet under samme forsøgsbetingelser.
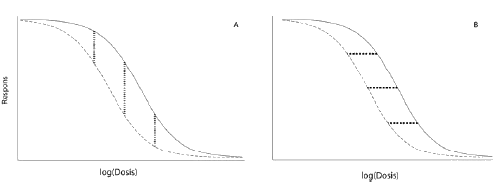
Figur 2.5. Den vertikale (A) og horisontale (B) sammenligning af to dosis-responskurver.
Den vertikale vurdering af to dosisresponskurver svarer i store træk til den måde man sammenligner effekter ved hjælp af en variansanalysemodel. I Figur 2.5A kan man se, at forskellene i effekter er særdeles påvirket af, hvilket dosisniveau man betragter. Det er klart ud fra Figur 2.5A, at forskellen mellem de to kurver (stiplede linjer) vokser som større doseringer, indtil forskellene igen forsvinder ved meget høje doseringer, fordi responsen på et tidspunkt vil gå mod en fælles nedre grænse.
Figur 2.5B viser den horisontale vurdering. Forskellen mellem de to kurver ved et givet responsniveau er vist vha. stiplede linjer og svarer til den relative styrke mellem to stoffer. Som det fremgår af de to kurver i dette specielle tilfælde, Den horisontale forskel eller afstand er ens for de tre viste responsniveauer i Figur 2.5B, men sådan behøver det ikke altid at forholde sig. To kurver siges at være parallelle, hvis de har de samme modelparametre undtagen den, der bestemmer deres placering på dosisaksen. Parallelforskydningen (afstanden mellem dosis-responskurverne) på log(dosis) aksen vil være ens for hele kurveforløbet. Dette er den gængse måde, hvorpå man vurderer og sammenligner effekten eller styrken af forskellige kemikalier inden for toksikologi. I dosis-responsforsøg med mange dosis-responskurver, er der yderligere den fordel ved den horisontale vurdering, at man ofte kan reducere opsummere forsøget vha. få parametre, der beskriver, hvordan kurverne ligger forskudt relativt til hinanden. Det er ved at benytte statistiske metoder, at man kan reducere antallet af parametre til et minimum. Hvis data tillader, at man kan antage parallelle dosis-responskurver, så er det nok at give ét relativt styrkemål, uanset hvilket responsniveau der betragtes (Ritz et al, 2006). Dette gælder også for responsniveauer tæt på den øvre og nedre asymptote. Eksempelvis er de to dosis-responskurver i Figur 2.5 parallelle, og derfor kan forskellen mellem dem opsummeres i et tal. Hvis kurverne ikke er parallelle, afhænger forskellene af hvilket responsniveau man betragter.
Version 1.0 Oktober 2008, © Miljøstyrelsen.