Guidelines on remediation of contaminated sites
Appendix
5.6
Risk assessment of groundwater - formulae for calculations
This Appendix provides an introduction to mixing, phase transitions, and spreading processes as they may occur in soil. More detailed descriptions can be found in literature, /1, 2, 3, 4, 5/.
For the saturated zone, a three-stage risk assessment is described.
| Stage 1 is a mixing model close to the source, based on the conservative assumption that the soil water at the bottom of the unsaturated zone has a contaminant concentration equal to the concentration strength at source. Subsequently, mixing in the uppermost 0.25 m of the groundwater aquifer is assumed. |
Alternatively, the resultant contamination concentration of the uppermost 0.25 m of the unsaturated zone can be directly determined by analysing groundwater extracted from a screen, which has been installed at the top of the groundwater aquifer.
| Stage 2 is a mixing model downgradient from the source, where increasing depths of mixing are assumed due to dispersion effects. |
| At Stage 3 the resultant contamination concentration of the groundwater is calculated while taking account of dispersion, sorption, and degradation in the saturated zone. Stage 3 is an extension of Stage 2, as the starting point for Stage 3 is the resultant contamination concentration calculated at Stage 2. |
The descriptions of models for substance spreading include a series of calculation parameters, some of which could be taken as standard parameters from Appendix 5.8, tables, or textbooks. Calculation parameters that typically have to be found in tables are designated as standard parameters in the text.
Examples of the use of the formulae indicated in connection with actual risk assessments can be found in Appendix 5.7.
A simple risk assessment cannot be outlined for the unsaturated zone. However, for the sake of comprehensiveness, equations for calculating substance concentrations (one-dimensional substance transport) in the unsaturated zone are provided.
1 Mixing model close to the source
No account is taken for neither sorption, dispersion, degradation, nor diffusion. It is assumed that the groundwater aquifer is homogenous (a one-layer model), and that the groundwater moves at constant speed.
The following section features these designations:
| N | 0 | net infiltration | [LT-1] |
| A | = | extent of the contaminated area | [L2] |
| B | = | contaminated area width | [L] |
| Co | = | concentration strength at source | [ML-3] |
| dm | = | mixing thickness | [L] |
| VD | = | Darcy velocity of groundwater | [LT-1] |
| Cg | = | Natural background contaminant concentration of groundwater | [ML-3] |
| k | = | hydraulic conductivity | [LT-1] |
| i | = | hydraulic gradient | [unitless] |
| Vp | = | average soil-water velocity for groundwater | [LT-1] |
The water flux Qo, percolating through the contaminated area can be described as follows:
Equation 1
Qo = N · A,
And the flux Jo of contaminants as:
Jo = Co · Qo = Co · N · A
When soil water infiltrates into the saturated zone, mixing occurs in the uppermost 0.25 m of the groundwater aquifer.
The groundwater flux Qg of water flowing below the contaminated area, consequently being contaminated by percolating soil water, corresponds to the groundwater held in a box with a length of VD (Darcy velocity of the water), a height of 0.25 m (mixing thickness) and a width of B (width of the contaminated area).
The groundwater flux Qg flowing below the contaminated area is then:
Equation 3
Qg = B · 0.25 · VD = B · 0.25 · k · i,
as VD = k · i, /1/.
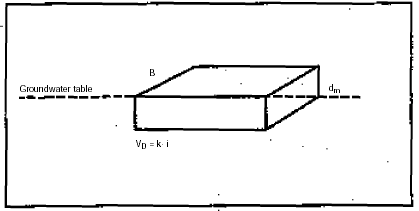
Figure 1
The flux of water below the contaminated area corresponds to the groundwater held in a
box with a length of VD (Darcy velocity of water), height of dm
(mixture thickness) and width B of the contaminated area.
When calculating the resultant contamination concentration of the groundwater, account must be taken of the fact that the groundwater may have a natural background concentration Cg of the contaminant.
For example, this applies to most metals.
The flux Jg of the natural contaminant content flowing with the groundwater below the contaminated area, can be expressed as:
Equation 4
Jg = Qg · Cg = Cg · 0.25 m · k · i × B
Where the background concentration of contaminants in the groundwater is caused by human activity at a different site, it should not be included in calculations. In these cases, Jg is set at 0.
The resultant contamination concentration C1 in the groundwater flowing immediately below the contaminated area can then be expressed as the total sum of the contributions from the percolating soil water and from groundwater flowing in.
Equation 5
![]()
Substituting the expressions from Equations 1-4 gives the following result:
Equation 6
![]()
In the expression for calculating the resultant contamination concentration C1, constant concentration at source Co throughout the entire area is assumed.
If the investigation phase indicates that there is basis for such a procedure, the contaminated site can be divided into sections with individual concentrations at source; contamination concentrations weighted by area.
For contamination covering large areas, calculations may concentrate on the central area of contamination. This is in accordance with the principle that the zone with the highest concentration in the groundwater must comply with the groundwater-quality criteria.
The resultant contamination concentration in the uppermost 0.25 m of the unsaturated zone can also be determined directly by analysing groundwater extracted from a screen (with a screen length of 0.25 m) installed in the top of the groundwater aquifer. With regard to further risk assessment, the highest value of the concentrations measured is used.
Attention must be given to the fact that executing a well with a 0.25 screen requires accurate knowledge of the position of the groundwater table in order for the screen to be placed accurately. See Section 5.4 of these guidelines.
A screen with a greater effective screen length than 0.25 m can be used for measuring the resultant contamination concentration at the top of the groundwater aquifer, if sampling is conducted at very low pumping capacity, so that no significant depression cone appears.
In cases where a screen with a screen length greater than 0.25 m is used, the resultant contamination concentration C1 in the uppermost 0.25 m of the aquifer must be calculated as follows:
Equation 7
C1 = C1,measured × 1/0.25 m
where C1,measured is the measured contamination concentration [ML-3] and 1 is the effective screen length (in metres).
2 Downgradient mixing model
The soil water at the bottom of the unsaturated zone is conservatively assumed to have a contaminant concentration equal to the concentration at source. Subsequently, mixing in the uppermost 0.25 m of the groundwater aquifer is assumed.
The resultant contamination concentration is calculated at a point found at a distance from the contamination source corresponding to the groundwater’s transport distance per year (calculations are made using the soil water velocity of the groundwater), up to a maximum of 100 m. At this theoretical calculation point, all values must comply the groundwater criteria.
The assumptions are the same as for the mixing model close to the source. No account is taken of sorption, degradation, or diffusion. The groundwater aquifer is assumed to be homogenous and isotropic ( a solo-stratum model), and the groundwater is assumed to maintain constant velocity.
The average soil-water velocity, which among other things is used when assessing the distance to the theoretical calculation point that must comply with the groundwater-quality criteria, is defined as follows:
Equation 8
VP = (k × i)/eeff
where
k = hydraulic conductivity [LT-1]
i = hydraulic gradient [unitless]
eeff = effective porosity; a standard parameter found in Appendix 5.8.
Based on tests involving the spreading of radioactive tracers, an expression for the mixing depth dm can be determined /4/:
![]()
![]()
where
DT,V is the downward dispersion coefficient [ L2T-1]
T is the transport time of the groundwater [ T] .
Under Danish conditions, as established e.g. from studies at the landfill at Vejen /1/, it is deemed to be a conservative estimate to say that DT,V = 1/900 DL, where DL is the longitudinal dispersion coefficient. As DL = a L × Vp the result is:
![]()
![]()
![]()
![]()
where
a L is the longitudinal dispersivity [ L]
Vp is the soil-water velocity [ LT-1]
T is the observed transport time [ T]
.
If the aquifer thickness is less than dm, the actual aquifer thickness must be used.
The longitudinal dispersivity varies with the distance from the source of contamination. Standard values are found in Appendix 5.8.
The transport time to the theoretical calculation point cannot exceed one year. The transport time to the theoretical calculation point will often be less than one year; this applies when the soil-water velocity Vp is greater than 100 m/year.
The designations used in the following are identical to those used at the first stage of the risk assessment.
The resultant contamination concentration C2 in the groundwater is calculated in a completely analogous fashion to the calculations for the first stage of the risk assessment, the downgradient mixing model.
Equation 10
![]()
![]()
The expression used for calculating the resultant contamination concentration C2 assumes a constant source-strength concentration Co throughout the entire contaminated area. As with Stage 1 of the risk assessment, the contaminated area can be divided into areas with separate concentrations at source, which corresponds to contamination concentration weighted by area.
In cases where the contamination concentration C1 in the uppermost 0.25 m of the groundwater aquifer has been measured during Stage 1, and any relevant subsequent corrections due to screen length have been made, this value can be used for simple calculation of the contamination concentration at a distance from the source C2.
At the relevant calculation point, the resultant contamination concentration C2 can be expressed as:
Equation 11
C2 = C1 × (0.25 m/dm)
= C1,measured × (l/dm)
where
Cl,measured is the resultant contamination concentration [ML-3] in the uppermost 0.25 m of the groundwater zone at the source of contamination; dm is the mixing thickness after one year of groundwater transport, at a maximum distance of 100 m downgradient of the contamination. If the mixing thickness is less than 0.25 m, dm = 0.25 m.
l is the effective screen length (in metres).
3 Downgradient mixing with degradation
Stage 3 of the risk assessment is an extension of Stage 2, as the starting point from Stage 3 is the resultant contamination concentration C2, which was calculated at Stage 2.
For this reason, the resultant contamination concentration is calculated, as was the case at Stage 2 of the risk assessment, at a point situated at a distance from the contamination source which corresponds to the transport distance per year of the groundwater (calculations are based on the soil-water velocity of the groundwater); up to a maximum distance of 100 m. At this theoretical calculation point, the groundwater-quality criteria must be complied with.
Whereas Stages 1 and 2 of the risk assessment are, as has been mentioned, conservative models, it is not possible to carry out strictly conservative calculations at Stage 3. For this reason, monitoring must be carried out where degradation is involved.
The saturated zone is assumed to be homogenous and isotropic and to have a constant groundwater velocity. Degradation and vertical dispersion is assumed to occur in the saturated zone.
It is assumed that the degradation can be described as a 1st order degradation. Calculations are carried out based on typical 1st order degradation constants, which are not necessarily conservative.
On the basis of 1st order degradation, the resultant contamination concentration C3 after degradation can be expressed as /1,5/:
C3 = C2 × exp(-k1 × t)
Where
C2 is the resultant contamination concentration as calculated in the downgradient mixing model at Stage 2 [ML-3]
k1 is the 1st order degradation constant in the saturated zone [T-1]
t is the period of degradation [T]
Typical 1st order degradation constants have only been compiled for the BTEXs, for some of the chlorinated solvents, and for phenol /5/. Degradation constants for these substances are found in Appendix 5.8.
Account can be taken of sorption in connection with an assessment of how long the contaminants are subjected to degradation. This is done by assuming that the contaminants move to the theoretical calculation point at a velocity Vs given by
Equation 13
Vs = Vp / R, R > 1
where
VP is the average soil-water velocity [LT-1]
R is the retardation coefficient [unitless]
The retardation factor can be calculated on the basis of the distribution coefficient Kd, which is a function of the organic content in soil foc and of the octanol-water distribution coefficient Kow. Values for Kow are found in tables, see Appendix 5.8. Based on the assumption that log Kow < 5 and foc > 0.1%, Kd can be calculated by means of Abdul’s formula /1/:
Equation 14
log Kd = 1.04 × log Kow + log foc – 0.84
The retardation factor can then be calculated by means of this formula:
Equation 15
R = 1 + r b/ew × Kd
where r b is the bulk density of soil [ML-3],
ew is the soil’s porosity when saturated with water [unitless], and Kd is the distribution coefficient.
As mentioned in the above, Stage 3 of the risk assessment, where degradation is involved, is not strictly conservative. For this reason, monitoring must be carried out in cases where the risk assessment shows that natural degradation of contaminants in the groundwater means that the standards of the groundwater-quality criteria can be met. This monitoring checks that degradation occurs in accordance with the assumptions. In addition to this, redox conditions must be determined, and data must be obtained to serve as the basis for calculating the relevant 1st order degradation constant.
When the rate of degradation is to be determined, it is necessary make corrections to the measured contamination concentrations to account for the effects of sorption, dispersion, dilution, etc. (non-destructive processes). This can be done by comparing concentrations of the contaminant with concentrations of a non-degradable substance (a tracer), or by comparing a slowly degradable contaminant and a more rapidly degradable contaminant.
Once the corrected contamination concentrations have been calculated, the 1st order degradation constant can be determined graphically by means of a t log-linear plot of the standard contamination concentration as a function of time. The 1st order degradation constant is determined as the slope of the linear section of the plot /5/.
In cases where the concentrations are known as functions of distance, rather than as functions of time, these figures can be converted by using the actual transport velocities that were determined during the contamination investigation.
The following addresses how the influences of non-destructive processes as regards the contamination concentration can be taken into account. This is done on the assumptions that the flux from the source of contamination is approximately constant, and that the groundwater aquifer is homogenous.
Measurements of concentrations of tracers and contamination made in two or more wells along a line of flow can be use to make an estimate of the contamination concentrations these wells would have had, if degradation were the only process attenuating the contamination.
An ideal tracer is influenced by non-destructive attenuation to the same degree as the contaminant (the tracer has the same volatility and same sorption coefficient as the contaminant), and the ideal tracer is not influenced by degradation processes.
Based on the assumption that an ideal tracer is utilised, the following equation describes the downgradient contamination concentration, where degradation has been the only attenuation process between the points i and i-1, placed downgradient along a line of flow (e.g. between the wells 3 and 2 in Figure 5.11) /5,6,7/:
Equation 16
![]()
where:
| Ci,corr | = | the corrected contamination concentration at point i. | |
| Ci-1,corr | = | the corrected contamination concentration at point i-1. (If i-1 is the first point (the point furthest upstream), Ci-1,corr is set at the observed contamination concentration at this point). | |
| Ci | = | the observed contamination concentration at point i. | |
| Ci-1 | = | the observed contamination concentration at point i-1. | |
| Ti | = | the observed tracer concentration at point i. | |
| Ti-1 | = | the observed tracer concentration at point i-1. |
On the basis of the contamination concentration at a measuring point positioned upstream, and on the basis of measurements of the relationship between concentrations of contaminants and tracers, this equation can be used to estimate the theoretical contamination concentration, which would result from degradation alone.
Equation 16 is conservative insofar as Ci,corr will be greater than Ci if the tracer is degraded. This will lead to the rate of degradation being estimated at lower values.
If the contamination concentration is corrected solely on the basis of tracer concentration between two points (A and B), Equation 16 is simplified:
Equation 17
![]()
A convenient method for estimating degradation constants is to utilise a non-degradable contaminant as a tracer. One such contaminant could be trimethylbenzene (TMB), which exists in three isomeric states (1,2,3-TMB; 1,2,4-TMB; and 1,3,5-TMB) generally present in fuels in sufficient quantities (3-7%) to be detectable in the groundwater /8,9/.
TMB is recalcitrant under anaerobic conditions, but is relatively easily degradable under aerobic conditions. TMBs degree of persistence is site-specific, and the usefulness of this contaminant as a tracer must be assessed in each individual case.
Tetramethylbenzene is another contaminant that can potentially be used as a tracer in connection with fuel contamination. However, tetramethylbenzene often appears in such small quantities that it is difficult to detect.
An ideal tracer has the same volatility and sorption coefficient as the contaminant under investigation, However, TMB has a greater sorption coefficient (and consequently a greater retardation coefficient) than BTEXs. For this reason, TMB is transported through the groundwater zone at lower velocities than the BTEXs.
Consequently, with a tracer like TMB it is necessary to modify equation 16 to take these differences of velocity into account. However, this modification is not necessary in stationary constant conditions (i.e. where the flux of the contaminant and tracer is constant at each point of measurement).
When a tracer is transported at a velocity that is significantly slower than the rate of spreading of the contaminant being investigated, concentrations of contamination and tracers must be assessed according to identical transport times instead of identical transport distances in order to take into account the degradation of the tracer as well as of the contaminant. The relationship between the velocities of tracer and contaminant can be expressed as:
Equation 18
![]()
where:
Vt = tracer transport velocity.
VS = contaminant transport velocity.
VP = groundwater velocity.
Rt = tracer retardation coefficient.
Rc = contaminant retardation coefficient.
The fraction of the tracer disappearing during the period of the contaminant moving from point i-1 to point i is represented by the expression Rc/Rt(1-Ti/Ti-1). That is to say that the remaining tracer fraction will be 1-Rc/Rt(1-Ti/ Ti-1).
In cases where the sorption of the tracer varies clearly from the sorption of the contaminant being investigated, the corrected contamination concentration at point i can be represented by the following equation:
Equation 19
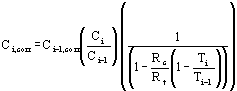
| Where: | Ci,corr | = | the corrected contamination concentration at point i. |
| Ci-1,corr | = | the corrected contamination concentration at point i-1. (If i-1is the first point (the point furthest upstream), Ci-1,corr is set at the observed contamination concentration at this point). | |
| Ci | = | the observed contamination concentration at point i. | |
| Ci-1 | = | the observed contamination concentration at point i-1. | |
| Ti | = | the observed tracer concentration at point i. | |
| Ti-1 | = | the observed tracer concentration at point i-1. |
Note that when Rc equals Rt, Equation 19 equals Equation 16.
As mentioned before, Equation 16 is conservative insofar as any degradation of the tracer will result in a low estimate of the rate of degradation. For this reason, with contamination with mixtures such as e.g. petrol, diesel, or similar substances, it will be possible to use one of the most persistent contaminants as a tracer, as low degradation of this contaminant will only lead to a more conservative estimate of the rate of degradation for the other contaminants.
4 Spreading in the unsaturated zone
Flow in the unsaturated zone of the soil is governed by gravitation and by capillary forces (differences in tension) dependant on soil-water content and on soil characteristics such as texture and soil-size distribution.
The following features equations for calculating contaminant concentration (one-dimensional contaminant transport) and substance-front velocity. Only contaminant transport with soil water is considered, and diffusion to air is discounted.
Actual cases of pulse addition are rare, and pulse additions to the unsaturated zone must often be seen as sources of continuous contamination of the saturated groundwater zone. For example, a broken oil tank can be said to give off pulse additions to the unsaturated zone. However, since the depth of the groundwater table causes a long transport period before the contamination front reaches the saturated zone, and since the dissolution of oil contaminants in infiltrating soil water is also a slow process, oil from a leaking oil tank will typically seep down to the groundwater zone over a period of decades. For this reason, seepage of oil components from a leaking oil tank to the saturated groundwater zone must usually be considered as continuous contamination.
With pulse addition of substances, the substance concentration in the unsaturated zone as a function of infiltration depth (z) and time (t), can be described by means of a one-dimensional contaminant transport equation /10/:
Equation 20
![]()
| where | z | is the depth of the calculation point [L], |
| ew | is the water content of soil [unitless], | |
| M | is substance addition [M/L2], | |
| DL | is the longitudinal dispersion coefficient in the unsaturated zone[L2T-1], | |
| t | is the time elapsed from the onset of contamination [T], | |
| Vp | is the pore velocity of water [LT-1]. |
The dispersion coefficient expresses the substance dispersion due to variations of flow
velocity in each individual pore, mixing due to variations in pore size along the
transport route, and molecular diffusion. Transversal dispersion is discounted.
The longitudinal dispersion coefficient DL can be determined by means of the soil-water velocity VP and the longitudinal dispersivity a L as follows:
DL = a L × VP
Standard values for the dispersivity a L are found in Appendix 5.8.
By continuous substance addition (one-dimensional substance transport), the concentration as a function of infiltration depth and time can be described as follows, /1,10/:
Equation 21

| where | z | is the depth of the calculation point [L], |
| C0 | is the concentration at source [ML-3], | |
| DL | is the longitudinal dispersion coefficient (standard data) [L2T-1], | |
| t | is the time elapsed from the onset of contamination [T], | |
| Vp | is the pore velocity of the water [LT-1]. |
Transversal dispersion is also discounted in this case.
The solution for the substance transport equation is approximate, and is only defined for t < Vp x z, where Vp x z is precisely the time lapse before the soil water reaches the saturated zone in cases where simple piston flow is assumed (no dispersion, sorption, or degradation).
Erfc is the complementary error function erfc(y) = 1 - erf(y), where erf(y) is defined as:
Equation 22
![]()
The substance-transport equations provided take no account of sorption. Modifications to the equations for substance transport are subsequently addressed to facilitate inclusion of the effects of sorption in calculations.
When calculating substance concentrations as functions of depth and time, the water’s pore velocity Vp is used for substances without the property of sorption. For substances with the property of sorption, this pore velocity is substituted by the propagation velocity of the substance front Vs, which can be described as follows:
Equation 23
![]()
where
| Vp | is the pore velocity of water [LT-1], |
| N | is the net infiltration [LT-1], |
| ew | is the water-saturated porosity [unitless], |
| Ru | is the retardation factor in the unsaturated zone [unitless]. |
See explanatory notes for Equation 13.
References
| /1/ | Kemiske stoffers opførsel i jord og grundvand
(‘Chemical Substance Behaviour in Soil and Groundwater’). Project on soil and
groundwater No. 20. The Environmental Protection Agency, 1996. [Tilbage] |
| /2/ | Bear, Jacob: Hydraulics of Groundwater. McGraw – Hill
Inc., 1979. [Tilbage] |
| /3/ | Grundvandskontrol ved kontrollerede affaldsdeponier
(‘Groundwater Monitoring by Controlled Waste Deposits).Dakofa, 1985. [Tilbage] |
| /4/ | Freeze, F og Cherry, J. A: Groundwater. Prentice – Hall,
Inc., 1979. [Tilbage] |
| /5/ | Kjærgaard, M., Ringsted, J.P., Albrechtsen, H.J. og Bjerg,
P.L. 1998. Naturlig nedbrydning af miljøfremmede stoffer i jord og grundvand
(‘Natural Degradation of Alien Substances in Soil and Groundwater’). Report
prepared by the Danish Geotechnical Institute and the Department of Environmental
Technololgy (Technical University of Denmark) for the Environmental Protection Agency. [Tilbage] |
| /6/ | Wiedemeier, T.H. et al. 1995. Technical Protocol for
Implementing Intrinsic Remediation with Long-Term Monitoring for Natural Attenuation of
Fuel Contamination Dissolved in Groundwater. Air Force Centre for Environmental
Excellence, Technology Transfer Division, Brooks Air Force Base, San Antonio, Texas. [Tilbage] |
| /7/ | Wiedemeier, T.H. et al. 1996. Technical protocol for
evaluating natural attenuation of chlorinated solvents in groundwater. Draft –
Revision 1. Air Force Centre for Environmental Excellence, Technology Transfer Division,
Brooks Air Force Base, San Antonio, Texas. [Tilbage] |
| /8/ | Christensen, L.B., Arvin, E. og Jensen, B. 1987.
Olieprodukters opløselighed i grundvand (‘Groundwater Solubility of Oil
Products’). Report for the Environmental Protection Agency. Laboratory of Technical
Hygiene, Technical University of Denmark. [Tilbage] |
| /9/ | Verschueren, K. 1983. Handbook of Environmental Data on
Organic Chemicals. 2. ed. Van Nostrand Reinhold. [Tilbage] |
| /10/ | Høgh Jensen, K. og Storm, B. Stoftransport i umættet og
mættet zone – simple beregningsmetoder (‘Substance Transport in Unsaturated and
Saturated Zones – Simple Methods of Calculation’). Stads- og havneingeniøren 2,
1985. [Tilbage] |