Guidelines on remediation of contaminated sites
Appendix
5.7
Examples of specific risk assessments of groundwater
This appendix features examples of how specific risk assessments have been carried out. The risk assessments are done in accordance with the principles indicated in Section 5.4 of these guidelines. The formulae applied in some of the calculations are described in Appendix 5.6. Standard calculation parameters can be found in Appendix 5.8, such as net precipitation, hydraulic conductivity, and 1st order degradation constants.
Example 1
Sand aquifer covered by clay
Turpentine contamination near the surface
Beneath thin layers of top soil and a layer of fill there is non-fissured clay to a depth of approximately 3.9 m below surface level. No signs have been found of any secondary aquifers in the clay. Beneath the clay is a meltwater sand aquifer to a depth of approximately 6.9 m below surface level.
The level of the groundwater table is at approximately 3.9 m below surface level, which broadly corresponds to the top of the sand stratum.
The sand stratum has a substratum of sticky tertiary clay. Figure 1 shows a geological cross-section of the site.
An enterprise producing wood preservatives operated on the site. Leakage from a faulty processing plant has caused turpentine contamination of the soil. This contamination has been found to be limited to a depth between 2.5 and 3 m below surface level.
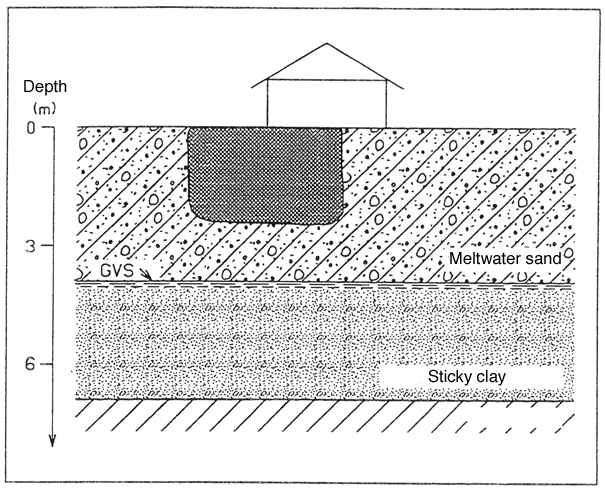
Figure 1
Cross-section showing geological conditions of example 1.
The contamination has spread all the way to the edge of existing buildings. Due to the very high cost of securing these building during the removal of soil, the contamination will only be dug away to a depth of 1.0 m below surface level
Soil samples from soil borings show concentrations of hydrocarbons of between 50 mg/kg and 800 mg/kg (quantified as turpentine) at depths of 1.0 to 3.0 m below surface level. This includes concentrations of single components up to: benzene 1.0 mg/kg, toluene 5mg/kg, and xylenes 12 mg/kg.
Figure 2 shows a map of benzene concentrations in the ground at 1.0 to 3.0 m below surface level. The concentrations indicated are maximum concentrations (mg/kg dry matter).
Present groundwater flow is generally south to south-west. Based on the assumption that the zone containing the highest concentration of contaminants in the groundwater must comply with the criteria for groundwater quality, the following risk assessment is carried out solely for the area that has been most affected by contamination (the area with a maximum benzene concentration of 1.0 mg/kg dry matter). This covers an area A of approximately 15 m x 8 m = 120 m2 .

Figure 2
Example 1. Maximum benzene concentrations (mg/kg dry matter) 1.0 to 3.0 m below
surface level.
Based on the surveys performed, the residual contamination of the area, after the removal of contaminated soil to a depth of 1.0 m below surface level, is estimated to comprise a maximum of 350 kg of turpentine (120 m2 x 2.0 m x 1,800 kg/m3 x 800 mg/kg), of this a maximum of 0.44 kg will be benzene.
Net precipitation in the region is approximately 240 mm a year (cf. Appendix 5.8). However, the groundwater division of the county authorities has carried out detailed groundwater models for the contamination area, and groundwater generation (net infiltration) of the site concerned is estimated at N = 100 mm/year. This means that percolation through the contaminated area is Q0 = A (the contaminated area) x N (net infiltration) = 120 m2 x 100 mm/year = 12 m3/year.
Had this detailed knowledge of groundwater generation not been available, it would have been necessary to utilise the figures for net precipitation when calculating percolation.
Based on the specific capacity of the water abstraction soil borings nearby, the transmissivity of the groundwater aquifer is estimated at T= 8 x 10-4 m2/s. With a saturated layer thickness of 3 m, this corresponds to a hydraulic conductivity of k = 2.7 x 10-4 m/s. The county authorities’ contour map of groundwater levels shows that the hydraulic gradient of the groundwater aquifer is i=0.004 in the direction towards the water works.
The pore velocity of the water is Vp = (k x i)/eeff = (2.7 x 10-4 m/s x 0.004)0.30, where eeff is the porosity of the groundwater aquifer, which in this case (a sand aquifer) has been set at eeff = 0.30 (cf. Appendix 5.8 – Table 1).
Dissolved oil products will be carried with percolating water through the unsaturated zone to the groundwater aquifer and onwards from here in the direction of the groundwater flow, i.e. in the direction of the water works’ abstraction wells.
Both the saturated and the unsaturated zones are aerobic, which indicates a potential for degradation.
This means that the relevant processes are solution, transportation, sorption, dispersion, and degradation in the saturated as well as the unsaturated zones.
Risk assessment
The following is a review of a step-by-step risk assessment carried out with a view to assessing the effect of the benzene contamination on the subjacent groundwater aquifer. The groundwater-quality criterion to be met in the groundwater aquifer is 1 m g/l.
Risk assessment is carried out solely for the single component benzene, as the spreading of this single component (which has very great solubility, and for which a very low groundwater criterion exists) is estimated to be critical for the groundwater resource.
At Stage 1, the soil water at the bottom of the unsaturated zone is conservatively estimated to have a contaminant concentration equal to the concentration at source. Subsequent calculations assume simple mixing in the uppermost 0.25 m of the groundwater aquifer.
A conservative mixing model is also used at Stage 2. The resultant contamination concentration is calculated at a theoretical calculation point positioned at a distance from the contamination source corresponding to the transport velocity of groundwater over a one-year period, to a maximum of 100 m. Calculations use a mixing density dm given by the equations in Appendix 5.6.
At Stage 3 of the risk assessment the resultant contamination concentration in the groundwater is calculated with consideration given to 1st order degradation. Stage 3 is an extension of Stage 2, as the point of departure is the contamination concentration determined at Stage 2.
Stage 1. Mixing model close to the source
Due to the difficulty of taking relevant water samples to determine concentrations at source, it has been decided to base the first stage of the risk assessment on simple considerations of solution and equilibrium.
The concentration at source has been calculated on the basis of an assumption of equilibrium between the phase distributions in water, air, and soil (the principle of fugacity). The calculation is carried out in accordance with the guidelines in Appendix 5.9. The calculations show that at a concentration in soil of 1.0 mg/kg DW, the benzene content in the soil-water is 5.0 mg/l (soil-particle density 2.7 kg/l; soil density 1.8 kg/l; volumetric proportion: soil 60%, air 10%, and water 30%).
As an alternative to land use of the principle of fugacity, the concentration at source can be set to equal the maximum solubility of benzene in water. However, as we have relatively low benzene concentrations in the soil, and as benzene is highly soluble in water, such an estimate will lead to far too great concentrations at source.
Conservative calculations must be made for the spreading of contamination. For this reason, it is assumed that no degradation or sorption of the oil products occur. Moreover, calculations disregard dispersion, i.e. are made for vertical percolation to the groundwater aquifer.
Benzene emissions with the infiltrating soil water from the remaining contamination will be approximately J0 = C0 × Q0 = 5.0 mg/l × 12m3/year = 60 g/year.
Benzene does not occur naturally in groundwater, and consequently the background concentration Cg in the groundwater is set at nil.
The resultant benzene concentration C1 in the uppermost part of the groundwater aquifer can then be calculated as stated in Appendix 5.6 – Equation 6:
![]()
Substituting the appropriate values results in:
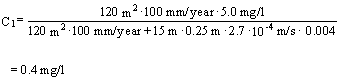
The quality criteria for groundwater for benzene is 1 m g/l; see Section 6.4 of these guidelines. On the basis of a risk assessment based on simple mixing and completely conservative estimates (no degradation, dispersion, or sorption), it follows that at the top of the groundwater aquifer, in the stationary situation, a benzene concentration must be expected which clearly exceeds the quality criterion for benzene.
At Stage 1 of the risk assessment, all parameters in the calculations are linear. That is to say that for each parameter, uncertainty has the same impact on calculations as for the other parameters – each parameter is equally important.
A simple assessment of the rate of leaching can be made by outlining a mass balance. The remaining contamination was assessed to consist of approximately 350 kg turpentine, of which 0.44 kg benzene. At the calculated concentration at source of 60 g/year for benzene, approximately 8 years will pass before the benzene contamination is removed. No assumptions of unrealistically rapid removal of the source of contamination have been made.
The risk assessment which has been carried out shows that the groundwater-quality criterion for benzene cannot be met in this situation.
The reason for this may be that the concentration at source C0 has been set too high due to a lack of analysis results. An option to consider, then, is to obtain analysis results from the uppermost area of the saturated zone from soil borings positioned immediately downgradient of the contaminated area, with very short (e.g. 0.25 m) screens installed in the uppermost area of the saturated zone. The very short screens are to ensure that inappropriate mixing with groundwater does not occur. There is a risk of this occurring, as the mixing depth is very small close to the source of contamination.
Another reason for the fact that the risk assessment shows that the groundwater criteria are not met may be that calculations are in general too conservative, as no account has been taken of sorption, dispersion, and degradation.
Stage 2. Downgradient mixing model
Stage 1 of the risk assessment provided the soil-water velocity Vp = 112 m/year. The theoretical calculation point is positioned at a distance from the source of contamination which corresponds to the groundwater’s transport distance in a year, up to a maximum of 100 m. Consequently, in this case the calculation point is positioned at the maximum distance of 100 m.
The mixing density dm is determined by (Appendix 5.6 - Equation 8):
![]()
The value for a L at a distance of 100 m from the source of contamination is determined from a figure (Appendix 5.8, Figure 2) at a L = 0.4 m.
The mixing time t = (100 m)/ Vp = 100 m/(112 m/year) = 326 days.
Substituting these values gives the following result:
![]()
= 1.8 m
In accordance with Appendix 5.6 – Equation 9, the resultant contamination concentration C2 at the theoretical calculation point can be expressed by:
![]()
The result after substitution is:
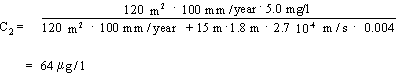
Using the downgradient mixing model also results in values exceeding the groundwater criterion of 1 m g/l.
A choice can now be made between various options: Implementing remedial measures, carrying out stage 3 of the risk assessment, or carrying out a risk assessment on the basis of new data; for example contamination concentrations measured in the uppermost area of the saturated zone.
Stage 3. Spreading model with dispersion, sorption, and degradation
The following describes stage 3 of the risk assessment, where biological degradation in the saturated zone is taken account of.
A prerequisite for utilising stage 3 of the risk assessment is sufficient knowledge of local geology and hydrogeology to facilitate optimum positioning (vertically as well as horizontally) of soil borings for sampling and monitoring in the contamination plume and directly downgradient of the contamination. The investigation phase must also have shown that the redox conditions provide opportunities for degradation of the contaminants in question.
For this reason, an additional contamination investigation has been carried out in order to obtain sufficient background knowledge. This investigation has provided detailed charts of the groundwater flow and redox conditions.
The additional investigation uncovered anaerobic conditions in the groundwater immediately below the spillage site. No oxygen content has been detected (< 0.1mg/l), Fe(III) contents are lower than in upstream soil borings, and methane has been generated.
However, oxygen contents increase rapidly both upstream, sideways, and downgradient of the contamination; 10-12 m downgradient, oxygen contents of more than 1 mg/l are found, i.e. aerobic conditions – see Section 5.4.
In the additional investigation, water samples have been taken from the uppermost part of the groundwater aquifer immediately below the spillage site. The effective screen length, l, was 0.75 m. The highest concentration of benzene was determined to be 6.4 m g/l.
According to Appendix 5.6, Equation 7, the resultant contamination concentration C2 in the most contaminated area of the groundwater zone at a distance of 100 m (mixing depth dm) can be expressed as:
| C2 | = | C1 × (0.25/dm) |
| = | 19.2 m g/l (0.25/1.8) | |
| = | 2.7 m g/l |
where:
| C1 | = | C1,measured (l/0.25 m) |
| = | 6.4 m g/l (0.75/0.25) | |
| = | 19 m g/l |
The groundwater-quality criteria of 1 m g/l is still not met.
The fact that there are aerobic conditions in the groundwater aquifer indicates a potential for degradation. The Fe(III)-reducing and methanogenic conditions around the spillage site indicate that natural degradation of the contamination is already occurring.
For this reason, it is relevant to include degradation in the calculations, and the resultant contamination concentration C3 after degradation, 100 m downgradient of the contamination, can be expressed as (Appendix 5.6 – Equation 12):
C3 = C2 × exp(-k1 × t)
The 1st order degradation constant k1 can (cf. Appendix 5.8) be set at 0.01-0.2 day–1. A conservative choice would then be k1 = 0.01 day-1.
When assessing the amount of time that contaminants are subjected to contamination, account may be taken of sorption. This is done by calculating the movement of contaminants towards the theoretical calculation point at the velocity Vs expressed by (Appendix 5.6 – Equation 13):
Vs = Vp / R, R > 1
Where:
VP is the average soil-water velocity [LT-1].
R is the retardation coefficient for benzene [unitless].
The retardation factor depends on the substances involved and on soil bulk density r b, actual content of organic substances in soil foc, and on the octanol-water distribution coefficient Kow. The contents of organic substances foc for various types of soil are found in Appendix 5.3, Table 1. Kow values for various substances are found in Appendix 5.5, Tables 1-5.
If log Kow < 5 and foc > 0.1%, the distribution coefficient Kd can be calculated by means of Abdul’s formula:
Log Kd = 1.04 × log Kow + log foc – 0.84
The retardation factor can then be calculated by means of the formula (Appendix 5.6 – Equation 15):
R = 1 + r b/ew × Kd
The following relevant values for benzene in a sand deposit are determined from tables (Appendix 5.5 – Table 1 and Appendix 5.3 – Table 1):
| Foc | = | 0.002 |
| Log Kow | = | 2.1 |
| Ew | = | 0.45 |
| r b | = | 1.8 |
which upon substitution provide the retardation factor for benzene:
| Rbenz | = | 1.2 |
| VS-benz | = | 93 m/year |
Of which t = 100 m/Vs-benz = 390 days.
The resultant contamination concentration C3 of benzene at the calculation point 100 m downgradient of the contamination is then:
| C3 | = | C2 × exp (-k1 × t) |
| = | 2.7 m g/l × exp (-0.01 × 390) | |
| = | 0.1 m g/l |
In this case, the groundwater quality criterion for benzene (1 m
g/l) is clearly met.
However, it is not sufficient to have calculations show that the quality criterion for groundwater is met. It is necessary to carry out monitoring which shows that the degradation of contamination occurs as predicted, and that the redox conditions continue to provide opportunities for degradation. Moreover, the current degradation constant should be calculated.
A number of soil borings were carried out in connection with the additional investigation. Four of these soil borings (designated A-D) are positioned on a flow-line downgradient of the contamination at distances from 4 to 37 m.
Selected monitoring data are shown in Table 1. As is apparent, there are aerobic conditions in soil borings B, C, and D (oxygen contents are greater than 1 mg/l), whereas there are low-oxygen conditions (probably anaerobic conditions) in soil boring A. This means that redox conditions have not changed since the additional investigation was carried out, and consequently there is still a potential for degradation of the benzene contamination.
The contamination concentration in the monitoring soil borings is less than expected. To check these values, the current degradation constant is calculated in accordance with Appendix 5.6.
Corrections are made to take into account sorption, dispersion, diffusion, etc.
The corrected contamination concentrations are determined by (Appendix 5.6 – Equation 19):
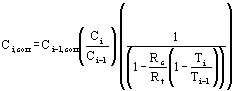
where:
| Ci,corr | = | corrected contamination concentration at point i. |
| Ci-1,cor | = | corrected contamination concentration at point i-1.(Where point i-1 is the first point (positioned furthest upstream), Ci-1,corr is set to equal the observed contamination concentration). |
| Ci | = | observed contamination concentration at point i. |
| Ci-1 | = | observed contamination concentration at point i-1. |
| Ti | = | the observed tracer concentration at point i. |
| Ti-1 | = | the observed tracer concentration at point i-1. |
| Rc | = | the retardation coefficient for the contaminant. |
| Rt | = | tracer retardation coefficient. |
Xylene is used as tracer, as xylene is degraded at a considerably lower rate than benzene
in this case. (see Table 1). The fact that xylene is degradable means that it is not an
ideal tracer, but this results in a conservative estimate; degradation is underestimated.
Table 1.
Selected data from 4 monitoring wells positioned on a line downgradient of the
contamination .
Monito-ring Well |
Downgradient distance |
Transport time benzene (days) |
Xylene content (m g/l) |
Benzene content (m g/l) |
Corrected benzene content (m g/l) |
Oxygen content (mg/l) |
A |
4 m |
0 |
12.0 |
6.4 |
6.4 |
0.3 |
B |
15 m |
43 |
9.2 |
2.4 |
2.7 |
1.7 |
C |
25 m |
82 |
6.5 |
0.7 |
0.9 |
1.8 |
D |
37 m |
145 |
5.0 |
0.09 |
0.13 |
2.1 |
Input data comprises values from Table 1and the previously calculated retardation
coefficient for benzene (RBenz = 1.2). Also used is the retardation coefficient
for xylene Rxyl, which is calculated correspondingly; Rxyl = 2.9.
To serve as an example, we calculate the contamination concentration in soil boring B with xylene corrections. Substitution results in:
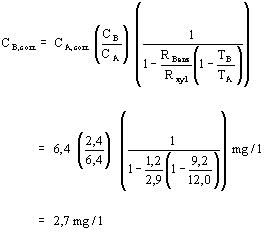
Benzene concentrations with xylene corrections are included in Table 1.
The corrected concentrations are then plotted into a log – linear plot as a function of the transport period from soil boring A (see Figure 1), and the 1st order degradation constant k1 is determined as the slope of the linear section of the curve.
Figure 3 shows how these points are really positioned on a straight line. This means that the requirement that degradation should be able to be designated as a 1st order degradation is met.
In this case, benzene concentrations drop from approximately 7.0 m g/l on day 0 to approximately 0.1m g/l after 150 days. The slope of the curve in Figure 3, and consequently the actual degradation constant, can then be determined as:
-k1 = ln(C/C0)/t = ln(0.1/7.0)/(150days) = -0.03 days-1.
This is to say that at the time in question, the actual degradation constant is greater than the conservative value used in the risk assessment. We are on the safe side.
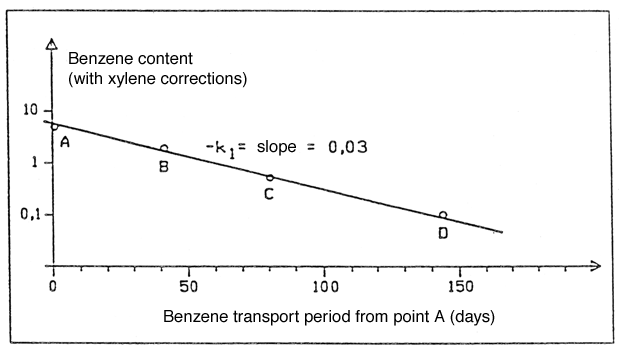
Figure 3
Plot of benzene content with xylene corrections along the flow line A, B, C. D.
Monitoring must be repeated to ensure that no changes occur, for example to the redox conditions, to stop or severely curtail degradation. As a minimum, monitoring must typically take place twice a year for three years.
Example 2
Sand aquifer covered by sandy clayey till
TCE contamination (Trichloroethylene)
A layer of fill of a 1.0 m thickness is uppermost. Below this are 2.0 metres of coarse sedimentary sand with a substratum of clayey till to a depth of approximately 8 m below surface level. The clayey till has a substratum of approximately 5 metres of sand and gravel. Beneath the lower sand stratum is sticky tertiary clay.
Figure 4 shows a geological section of the site.
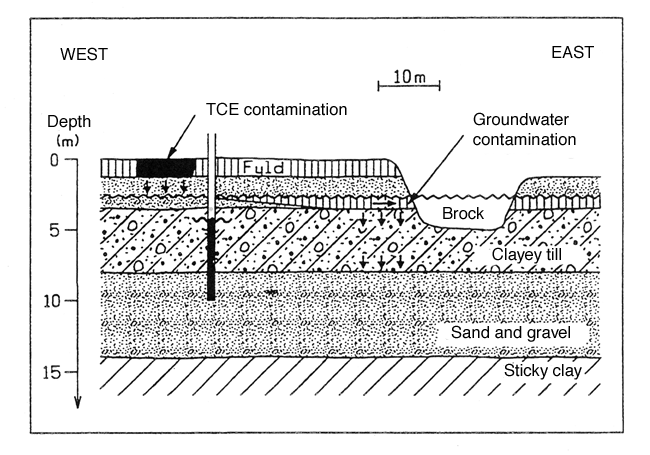
Figure 4
Section showing the geological conditions of example 2
There is a upper as well as a lower groundwater aquifer. The upper aquifer is situated in the upper sand stratum. The aquifer is unconfined with a water table level situated approximately 2.5 metres below surface level.
A brook flows approximately 40 metres east of the survey area. The groundwater flow in the upper aquifer flows towards this brook with a hydraulic gradient i = 0.006; as established from observation of water levels in wells. Net precipitation N is estimated at 200 mm a year (cf. Appendix 5.8). On this basis infiltration through the contaminated area can be established as Qo= A (the contaminated area) x N (net precipitation) = 60 m2 x 200 mm/year = 12 m3 /year.
County groundwater authorities estimate the hydraulic conductivity k of the upper aquifer at k = 2.5 x 10-4 m/s.
The average pore water velocity Vp in the upper groundwater aquifer can then be set at (cf. Section 5.6 – equation 8):
| Vp | = | (k x i)/eeff |
| = | (2.5 x 10-4 m/s x 0.006)/0.30 | |
| = | 157 m/year |
where eeff is the effective porosity of the groundwater aquifer, which in this
case has been set at 0.30 (cf. Appendix 5.8 – Table 1).
The lower sand stratum constitutes the lower groundwater aquifer. The aquifer has a head approximately 3.5 m below surface level. That is to say that there is a pressure difference of approximately a 1.0 m water column between the lower and the upper aquifer, and a downward gradient.
On the basis of test pumping, hydraulic conductivity k of the lower groundwater aquifer is estimated at : k = 3.6 x 10-4 m/s. The hydraulic gradient is determined as: i = 0.005; as with the upper aquifer, the groundwater flow runs broadly to the east.
The average pore water velocity Vp of the water of the lower groundwater aquifer can now be determined as (cf. Appendix 5.6 – equation 8):
| Vp | = | (k x i)/eeff |
| = | (3.6 x 10-4 m/s x 0.005)/0.30 | |
| = | 190 m/year |
where the effective porosity eeff = 30 % has been established previously in
connection with a nearby abandoned water work well.
It has been established that the layer of fill contains trichloroethylene (TCE) in an area A covering approximately 50 m2 (approximately 12 m x 4 m) and throughout the entire depth of the layer of fill (i.e. 1.0 m). TCE concentrations are between 4 to 6 mg/kg dry matter, i.e. almost evenly distributed. The soil quality criteria for TCE is 5 mg/kg dry matter (Section 6.2 of these guidelines), so the concentrations found were actually similar to these soil-quality criteria.
However, since the test area has been designated as a car park, the area is not deemed to pose any risk to this form of land use.
No TCE has been detected in the underlying intact soil layer.
On the basis of the surveys performed, contamination is estimated at a maximum of 50m2 x 1 m x 1.7 tonnes/m3 x 6 mg/kg = 0.5 kg.
The concentration at source C0 can be calculated on the assumption of equilibrium exists between the phase distributions in soil, air, and water (the principle of fugacity). This calculation, made in accordance with the directions found in Appendix 5.9, show that at a TCE concentration in soil of 6 mg/kg dry matter, the TCE content of pore water (concentration at source C0) is approximately 8 mg/l (the particle density of the soil is 2.65 kg/l; the density of the soil is 1.7 kg/l; volumetric proportions: soil 55%, air 30%, and water 15%).
The only nearby recipient in the direction of the flow is a brook approximately 40 m downgradient of the contaminated area.
The upper aquifer is of no interest with regard to water abstraction. For this reason, risk assessment will only address contamination hazards to the lower aquifer and the nearby brook.
The width of the vertical dispersion zone dm of the upper groundwater aquifer can be determined as (Appendix 5.6 – equation 9):
![]()
At the brook (a distance of approximately 40 m from the contamination) the following vertical width is found:
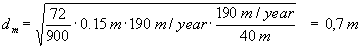
where a L = 0.15 has been read off from Figure 2 in Appendix 5.8, and time of flow t= 190 m/year/40 m.
As the upper aquifer is only 0.5 m thick, this means that the contaminants are mixed throughout the entire thickness of the aquifer before the groundwater reaches the brook.
Similarly, the zone of dispersion at a distance of 30 m downgradient of the contamination can be calculated as:
![]()
In terms of these calculations, we have reached mixture of the contaminants throughout the upper aquifer 30 m downgradient of the contamination.
This means that the leach area, defined as the area where leaching from the upper aquifer through the clayey till to the lower groundwater aquifer takes place, extends from 30 to 40 m downgradient of the contamination, since the upper aquifer is cut off by the brook 40 m downgradient of the contamination.
The resultant contamination concentration Cs of the upper groundwater aquifer at a distance of 40 m from the contamination source (i.e. just as the groundwater reaches the brook) can be calculated as (Appendix 5.6 – equation 10):
![]()
TCE does not occur naturally in groundwater; hence the background concentration Cg of the groundwater is zero.
Substituting into the equation gives :

= 270 m g/l
A simple estimate of the rate of leaching can be made by a mass balance consideration. Residual contamination was estimated to comprise approximately 0.5 kg TCE. With a source strength J of J = N x A x C0 = 50 m2 x 200 mm/year x 8 mg/l = 80 g/year it will take approximately seven years to leach the TCE contamination. This means that the speed at which the source of contamination is removed is not unrealistic.
The above calculations show that the groundwater flowing from the upper aquifer into the brook has a TCE content of 270 m g/l.
We have also calculated that each year the contamination leaches an amount of TCE determined as:
| A x N x | = | 50 m2 x 200 mm/year x 8 mg/l |
| C0 | = | 80 g/year |
County authorities’ recipient division informs us that the brook’s flow of water
Qmin at median minimum is approximately 2 l/second. In the brook, that has a
flow of water corresponding to median minimum, the contaminated groundwater is diluted due
to mixing. This gives a TCE concentration Cbrook of:
| Cbrook | = | A x N x C0/Qmin |
| = | 80 (g/year)/ 2 (l/second) | |
| = | 1.27 x 10-3 m g/l |
On the basis of the calculations performed, the county recipient division’s
assessment is that the TCE leaching into the brook does not pose any risk in relation to
the objectives for the recipient.
The vertical velocity (Darcy velocity) VD of the groundwater can be determined as (cf. Appendix 5.6 – equation 3):
VD = k x i
As with horizontal flow, the hydraulic gradient is expressed as the difference in water level D h (in this case between the two aquifers) divided by the difference in distance D s (in this case the vertical distance). We have:
| I | = | D h/D s |
| = | (3 m – 2 m)/(8m – 3 m) | |
| = | 0.2 |
The vertical hydraulic conductivity can be established by looking it up in Appendix 5.8,
Table 1. The lower boundary of the clayey till stratum determines hydraulic conductivity.
In this case, the clayey till stratum goes down to a depth of 8 m below surface level.
By interpolating the values of the table, k is determined as 1 x 10-8 m/second.
This means that the vertical Darcy velocity is
| VD | = | 0.2 x 10-8 m/second |
| = | 60 mm/year |
Seen in relation to the fact that net precipitation is 200 mm/year, vertical velocity in
the clayey till seems quite high, but still possible.
The flux J of TCE through the clayey till can be calculated as (Appendix 5.6 – equation 1):
| J | = | VD x A x Cs |
| = | 60 mm/year x 10 m x 12 m x 270 m g/l | |
| = | 1.9 g/year |
This flux through the clayey till does not seem unrealistically large when compared to the
flux down towards the upper groundwater aquifer. It should, however, be noted that using
table values for vertical hydraulic conductivity creates scope for considerable
uncertainty.
For instance, if we take the example above and substitute a vertical hydraulic conductivity of e.g. 10-7 m/s (instead of 10-8), this will provide us with a vertical Darcy velocity of 600 mm/year. This is three times more than the net precipitation and hence totally unrealistic.
Analogously to Appendix 5.6, equation 6 (Step 1 of risk assessment), the contamination concentration CP1 in the upper 0.25 m of the lower groundwater aquifer immediately below the percolation area (which is 30 – 40 m downgradient of the contamination) can be determined as:
![]()
Where
| A | = | The percolation area (through the moraine clay); 120 m2. |
| VD | = | Vertical Darcy velocity 60 mm/year. |
| Cs | = | Contamination concentration of the upper groundwater aquifer (where the aquifer has full mixture); 270 m g/l. |
| B | = | Breadth of soil contamination; 12 m. |
| K | = | Horizontal hydraulic conductivity of the lower aquifer; 3.6 x 10-4 m/s. |
| i | = | The hydraulic gradient of the lower aquifer 0.005 |
If these values are substituted, the result is:
CP1 = 11.0 m g/l.
The groundwater quality criteria of 1m g/l is exceeded immediately below the percolation area.
For this reason, we apply the second step of risk assessment to the lower groundwater aquifer.
At an earlier stage, we calculated the average pore water velocity in the lower aquifer VP to be 190 m/year. In the second step of risk assessment we need to calculate the contamination concentration at a point downgradient of the contamination at a distance corresponding to a year of groundwater flow (to a maximum of 100 m). In this example, the theoretical point of calculation is 100 m downgradient of the contamination.
The percolation area, i.e. the area where the clayey till has been infiltrated by TCE contaminated groundwater, is 30-40 m downgradient of the contamination.
That is to say that the theoretical calculation point is only 60 m away from the leach area.
The vertical dispersion zone dm can now be determined as (Appendix 5.6 – equation 9):
![]()
where a L = 0.21 has been read off from Figure 2 in Appendix 5.8, and degradation time t = (60m/190m/year)).
According to Step 2 of risk assessment (Appendix 5.6 – equation 10), the contamination concentration CP2 of the lower groundwater aquifer 100 m downgradient of the contamination can be calculated as:
![]()
If we substitute the values, the result is:
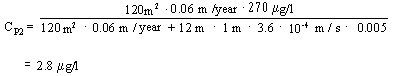
This means that upon completion of Step 2 of the risk assessment, the contamination is still deemed to present a hazard to groundwater resources.
In order to carry out Step 3 of risk assessment (see Section 5.4 of these guidelines), it is necessary to have the knowledge of geological and hydrogeological conditions required to facilitate optimum location of wells for surveying and monitoring. Complicated flow conditions around the brook prevent these requirements from being met. Due to this, Step 3 of the risk assessment process will not be carried out.
Example 3
Sand aquifer without cover
Arsenic contamination
Below a thin cover of top soil is meltwater sand to a depth of approximately 5.0 m below surface level. Underlying the sand layer is a layer of sticky clayey till.
Figure 5 shows a geological section of the site.
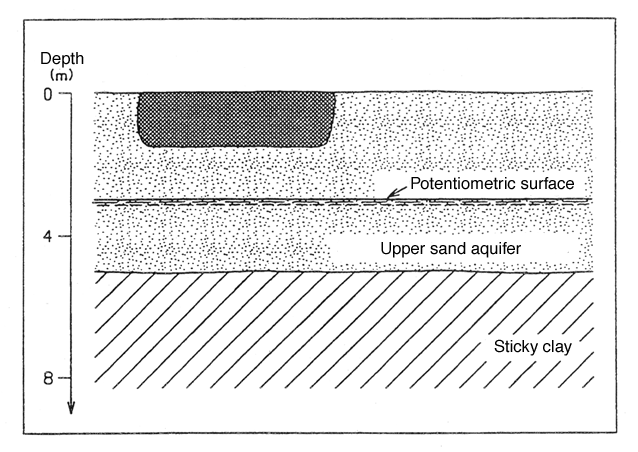
Figure 5
Section showing the geological conditions of example 3.
An area A of approximately 80 x 40 m has been contaminated by arsenic to a depth of approximately 1.5 m below surface level. The contamination was caused by leakage from a wood-preservation plant which was abandoned in the 1950s. The contaminated area is situated in a park-like area located close to built-up areas.
In general, the concentration of contamination in the area is around 50 mg/kg dry matter. There is, however, a hot spot where As concentrations of up to 1,200 mg/kg dry matter have been detected. This hot spot can be recognised from surface level to a depth of 0.5 m below surface level.
Since additional costs will be modest, the top 0.5 m of soil will be removed throughout the entire contaminated area. Re-establishing the area with uncontaminated soil will ensure that the top 0.5 m will be in accordance with the soil quality criteria of 20 mg/kg dry matter and the eco-toxicological soil quality criteria of 10 mg/kg dry matter (see Section 6.2 and 6.3 of these guidelines).
As regards usage of the site, the area is subject to administrative regulation preventing exposure to contaminants.
Total arsenic content of the soil is estimated at 3,200 m2 x 1m x 50 mg/kg x 1.7 kg/m3 = 270 kg.
Leaching surveys have previously been carried out from hot spots showing that pore water concentrations C0 of up to 2 mg/l must be expected.
Groundwater monitoring shows that the natural arsenic content of the area’s groundwater is under 2 m g/l. The groundwater quality criteria for arsenic is 8 m g/l (see Section 6.5 of these guidelines).
The sand stratum constitutes an unconfined upper groundwater aquifer, and the groundwater table is situated approximately 3.0 m below surface level.
Downgradient of the survey area are several individual water-abstraction sites from the upper aquifer. This means that the aquifer must be protected as a groundwater resource.
On the basis of data from the abstraction wells, the hydraulic conductivity k of the aquifer is estimated at k = 5 x 10-4 m/s; the hydraulic gradient is estimated a 0.005, and effective porosity eeff at 25 %.
Net precipitation N is set at 180 mm/year (cf. Appendix 5.8).
The groundwater’s average pore water velocity Vp can be determined as (Appendix 5.6 – equation 8):
| Vp | = | (k x i)/ eeff |
| = | (5 x 10-4 m/s x 0.005)/0.25 | |
| = | 315 m/year |
There are no downgradient recipients within the nearest 1,500 m.
A simple estimate of the rate of leaching can be made by a mass balance consideration. Residual contamination was estimated to comprise approximately 270 kg of arsenic. With a source strength J of J = A x N x C0 = 3,200 m2 x 180 mm x 8 mg/l = 1.15 kg/year it will take slightly more than 200 years to leach the arsenic contamination. This does not seem unrealistic.
The contamination concentration C1 in the uppermost 0.25 m of the aquifer immediately below the contamination can according to Appendix 5.6 – Equation 6 be calculated as:
![]()
Substituting the appropriate values results in:
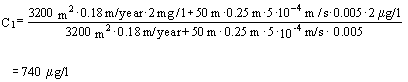
Where the width of the soil contamination B (50 m) is measured perpendicular to the direction of the groundwater flow.
This means that with the outlined assumptions, stage 1 of the risk assessment offers up resultant contamination concentration which are far greater than the groundwater quality criteria.
For this reason, stage 2 of the risk assessment is carried out.
After carrying out stage 1 of the risk assessment, a number of investigation soil borings with screen installations have been conducted in the groundwater aquifer.
The greatest arsenic concentration in the groundwater was found immediately below the soil contamination. An arsenic concentration C1 of 45 m g/l was observed in a screen with an effective screen length l of 0.75 m.
In stage 2 of the risk assessment, the resultant contamination concentration is calculated for a theoretical calculation point which is situated at a distance from the contamination source corresponding to the annual soil-water transport distance (to a maximum of 100 m). In this case, a soil-water velocity VP of 315 m/year was found. For this reason, the calculation point in this context is situated at the maximum distance of 100 m from the contamination source.
According to Appendix 5.6 – Equation 9, the mixing density dm at a distance of 100 m can be determined as:
![]()
![]()
= 1.8 m
where a L is found in Figure 2 in Appendix 5.8, and t = 100 m/(315 m/year).
The resultant contamination concentration C2 in the theoretical calculation point positioned 100 m downgradient of the contamination can then be calculated as (cf. Appendix 5.6 – Equation 11):
| C2 | = | C1 × (0.25 m/dm) |
| = | 135 m g/l × (0.25/1,8) | |
| = | 19 m g/l |
where
| C1 | = | C1,measured × (1/0.25 m) |
| = | 45 m g/l × (0.75/0.25) | |
| = | 135 m g/l |
So stage 2 of the risk assessment also comes up with resultant contamination
concentrations greater than the groundwater criteria.
Arsenic is an element and as such cannot be degraded (only changes in its chemical form can occur). For this reason it is impossible to carry out stage 3 of the risk assessment, where degradation is included in calculations.
For this reason, remedial measures should be taken, as the contamination poses a threat to the groundwater resource.