Scenarios and Model Describing Fate and Transport of Pesticides in Surface Water for Danish Conditions
8 Uncertainty Analysis of the Registration Model
8.1 General systematic in uncertainty analysis
8.2 Principle of the uncertainty analysis - intelligent Monte Carlo
8.3 Uncertainty on the quantification of the variance
8.4 Implementation in to the user interface
This chapter sum up the detailed uncertainty evaluation performed in Appendix D. The chapter is complementary to Chapter 7. Hence Chapter 7 covers various aspects of uncertainties with regard to the scenarios and how well the implemented matematical functions describes the condition in the catchments. The aim of the current chapter is to provide an approach for how to cope with the uncertainty or variation associated with the pesticide specific parameters. To facilititate a dicrimination between the uncertainties considered in Chapter 7 and in the present chapter a short general discussion of the various types of uncertainty is provided in Section 8.1.
8.1 General systematic in uncertainty analysis
The uncertainty of the model predictions is crucial when models are applied in decision-making. Some kind of uncertainty estimate is therefore needed before the model system can be said to have predictive power because it is not possible to evaluate a calculated property if no information about the uncertainty exists. However, it is difficult and in practise even impossible to perform complete uncertainty estimates that take all sources of model uncertainty into account. But this does not mean that the model uncertainty cannot be evaluated. The task is to gather as much information as possible about the model uncertainty before the model system is applied.
There exist two principally different sources of uncertainty relating to the predictive model itself:
- Structural uncertainty arising form the assumptions needed for the model equations to describe the phenomenon in question.
- Input parameter uncertainty as a consequence of variability and lack of knowledge.
Methodologies for performing structural and input parameter uncertainty estimates are different. The structural uncertainty can only be truly estimated in cases where the total uncertainty on input parameters is known and the model predictions can be compared with “reality” at the same time. This introduces the need for high quality data to validate the model and will not be a part of this work. It is however important to emphasise that if sufficient data are available to make a complete determination of the structural uncertainty, then data are needed for all possible model outcomes and in these cases there is hardly any need for predictive models for decision making. The structural uncertainty is dealt with in details in Chapter 7 whereas the uncertainty of the pesticide specific input parameters is the topic for the present chapter.
Straightforward methods for quantifying the input uncertainty, point 2, exist, typically by using a Monte Carlo type analysis (see Figure 8.1). But they often involve laborious calculations for larger models such as the registration model. The topic for this part of the work is to set up guidelines in order to make it possible to evaluate model outcome uncertainty of the registration model.
It is important to emphasise that analysis of input uncertainty needs to be done carefully in order not to create false realism. Uncertainty analysis for predictive models is often by itself rather uncertain, where the uncertainty estimates are associated with uncertainty. The uncertainty analysis will tend to underestimate the “true” variability due to the missing of quantification of the structural uncertainty, considered in Chapter 7.
8.2 Principle of the uncertainty analysis – intelligent Monte Carlo
The purpose is to assess the uncertainty of the calculated pesticide concentrations in the stream and pond compartments as a function of the uncertainties on input parameters. A Monte Carlo analysis can be performed as illustrated in Figure 8.1. Repeatedly the model will be run using a random selected value for every input parameter in the analysis and Figure 8.1 shows how to perform one single run. The variability of the modelling result reflects the uncertainty due to pesticide specific input parameters. If all possible input parameters in a large model are going to be investigated using this type of analysis then often an unrealistic large number of model runs are needed. So, a critical aspect is to select a limited number of input parameters for the uncertainty analysis in a way so the major part of the uncertainty is accounted for.
In most cases a single or a few processes, depending on the environmental conditions and the properties of the actual pesticide, will control the modelling result. For the stream/pond part of the model (MIKE 11) simple relationships have been derived to identify such a dominance (Appendix D), which will be helpful in order to focus the uncertainty analysis to a few controlling parameters. In brief the simple relationships consist of a simple version of the MIKE 11 module, which do not take the spatial variation and varying boundary and forcing functions in to account. In addition the differential equations of the model was solved analytical through assumptions of quasi steady state condition in the stream. The result of this analysis is presented as decision tress, which appears from Figure 8.2 to Figure 8.4.
The registration model comprises a soil module (MIKE SHE), which defines the pesticide input concentration to the surface water module (MIKE 11). It have not been possible to derive a simple model for the soil module, MIKE SHE, as for the MIKE 11 module and decision trees for the MIKE SHE part of the model can therefore not be made. The choice of process of relevance for the uncertainty analysis therefore had to be selected through other means. However, the MIKE SHE module only comprises two processes, sorption and degradation, whereas the MIKE 11 module comprises eight processes for which consideration of the uncertainty is relevant. Hence a selection of process seems most relevant for the stream/pond part of the model. Furthermore the calibration exercise (Styczen et al., 2004a) revealed that the concentration in the stream mainly is determined by the process in the MIKE SHE model, which is readily explained the longer residence time of the pesticides in the soil compartment compared to the stream. It was therefore decided always to include the uncertainty of the process, sorption and degradation, of the MIKE-SHE model in the uncertainty analysis.
To reduce the number of model runs further the sampling within a gaussian random field was substituted with a Latin Hyper Cube sampling of Gaussian fields (Pebesma and Heuvelink, 1999).
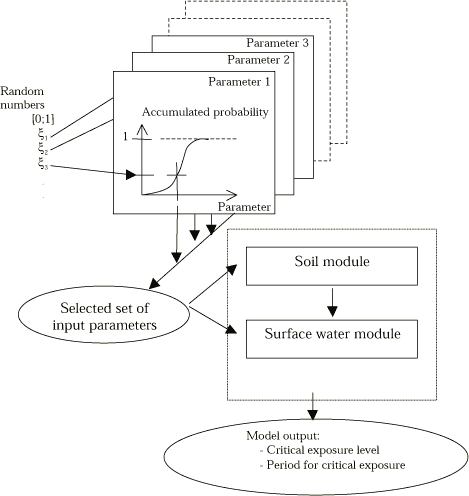
Figure 8.1 Principles for uncertainty analysis based on Monte Carlo simulations. Input parameters are typically assumed being normal or log-normal distributed. The endpoint is uncertainty estimates on critical stream output parameters.
Figur 8.1. Principper for usikkerhedsanalyse baseret på Monte Carlo-simuleringer. Input parametre forventes at være normal- eller log-normalfordelt. Endepunktet er usikkerhedsestimater på kritiske å-resultat-parametre.
8.3 Uncertainty on the quantification of the variance
To conduct the intelligent Monte Carlo analysis the selected pesticide specific parameters needs to be associated with a standard deviation or variance. In addition the pesticide data from the legislation, stored in the PATE database, will form the basis for the model. These data includes data derived from different laboratories, using different analytical as well as different empirical/statistical models for interpretation of the experiments. To conduct the uncertainty analysis across process on a common basis it is therefore assumed that the experiment is used as the unit of replication when the standard deviation or variance is calculated. In addition is it assumed that the log transformed data follows a normal distribution. The log transformation was needed to avoid a larger numbers of negative estimates of the process parameters.
The uncertainty on input parameters can be then estimated by evaluating the following two topics:
- Uncertainty due to the assumed functional form of the stochastic relationship for input parameter variability.
- Missing information due to the limited number of single data values to estimate the variability of the input parameters.
The type A uncertainty can e.g. be the result of an assumed normal or equal distribution of input data. It has not been possible to evalute whether this assumption is fullfilled on a sound basis, due to a limited number of data. However, a log-normal distribution is frequently used for probabilistic risk assessment and the assumption is thus in line with this practice (Solomon et al 1996, Hall et al., 1996). When the distribution function for the input data is assumed known then the type B uncertainty arises from the fact that the distribution-function parameters (e.g. mean value and variance) needs to be estimated based on a limited number of data values. To overcome point B it is the intention to substitute the log-normal distribution with a t-distribution fitted to the log transformed input data.
8.4 Implementation in to the user interface
Due to logistic constraints caused by the calculation time of the model it is not considered relevant to implement uncertainty analysis in the user interface at the current state. Hence an uncertainty analysis would last for about a month if 25 runs should be conducted as a part of the intelligent Monte Carlo. Instead a spreadsheet deriving relevant input data on the basis of the pesticides properties and the variations thereof have been produced and will be delivered together with the model. In brief the spreadsheet comprise an operationalization of the descision trees through logical (if ..then else..) functions, whereby the input parameters for which the uncertainty is most important for the output of the model is pointed out. The second part of the spread sheet produce 25 sets of input parameters through a Latin Hyper Cube sampling of the selected parameters.
Click here to see Figure 8.2 – 8.4.
Figure 8.2 The decision tree for selecting controlling stream process parameters in relation to the calculated dissolved concentration in the stream.
Figur 8.2 Beslutningsstøtte-træ til selektion af parametre, der kontrollerer å-processer in relation til den beregnede koncentration af opløst stof i vandløbet.
Figure 8.3 The decision three for selecting the controlling parameters for the calculated adsorbed concentration in the sediment.
Figur 8.3 Beslutningsstøtte-træ til selektion af parametre, der kontrollerer den beregnede koncentration af adsorberet stof i sedimentet.
Figure 8.4 The decision tree in relation to the dissolved concentration in the pond model.
Figur 8.4 Beslutningsstøttetræ i relation til opløst koncentration i vandhuls-modellen.
Version 1.0 Maj 2004, © Danish Environmental Protection Agency