[Front page] [Contents] [Previous] [Next] |
Ecotoxocicological assessment of antifouling biocides and non-biocidal antifouling paints
Appendix 1: Model for calculation of exposure concentrations (PEC)
1. Introduction
2. Establishing af calculation model
2.1 Scenarios
2.2 Emissions of antifoulants
2.3 PEC model
2.4 Data on active substances
2.4.1 DCOI
2.4.2 Zine pyrithione (ZPT)
3. Calculation results
4. Sensitivity materials
4.1 Harbour scenarios
4.2 Sensitivity analysis of other parameters
1. Introduction
This appendix describes the exposure model which was used for calculating the exposure concentrations PEC (Predicted Environmental Concentration) for DCOI and zinc pyrithione (ZPT) and their main metabolites.
The established model applies modelling principles that are generally used at the determination of PEC. Numerous models for calculating exposure are described in literature, i.a.:
| SimpleBox, which is a "multi-compartment" model based on the fugacity principle (Fredenslund et al. 1995). This model is used in the Technical Guidance Document (TGD) for generic risk assessments of individual substances (EC 1996) and is thus incorporated in the edp model EUSES, which is an "electronic" edition of the TGD (European Chemicals Bureau 1997). | |
| Furthermore, EUSES includes a module for estimation of PEC for antifoulants. | |
| The CHARM model, which is used for risk assessments of offshore chemicals (Karman et al. 1996). | |
| EXAMS, which is an interactive computer program for simulation of the fate of environmentally hazardous substances in aquatic ecosystems (Burns et al. 1981). |
2. Establishing a calculation model
In general, exposure assessments are composed of the following items:
Setting up of scenarios describing the environmental parameters of importance to the emission and the fate of the substances | |
Determination of the emission of chemicals | |
Calculation of PEC in relevant sub-environments | |
Sensitivity analysis in which the relative dependency of PEC of the parameters forming part of the standard scenarios and the relative dependency of PEC of the parameters of the substances are estimated. |
These elements were also applied in the present exposure calculations.
2.1 Scenarios
Two standard scenarios have been set up for the calculation of exposure concentrations (PEC):
| 1. | Pleasure craft harbour. The pleasure craft harbour of Jyllinge has been chosen as standard pleasure craft harbour. This pleasure craft harbour was selected as a realistic worst-case as the harbour has a large number of boats compared to the water volume of the harbour and a low water exchange. The whole harbour area is included in the scenario and total mixing is assumed for the entire harbour area. |
2. |
Busy navigation route. The narrows of Kronprins Frederiks Bro (near Frederikssund) was chosen as standard navigation route. Partly because there is relatively heavy traffic of pleasure craft and partly because statistics have been made of the number of boats passing the bridge. The scenario comprises a water column with a length of 1 metre in the sailing direction and a width similar to that of the boats. Total mixing is assumed in the vertical direction of the water column. |
Both standard scenarios are thus placed in Roskilde Fjord.
Each scenario was characterized as regards:
Water exchange
|
For both scenarios, the concentration of substance in the water transported into the waters in question is considered insignificant.
Water depth. | |||||
Composition and characterization of suspended matter. The suspended matter was characterized with respect to the contents of organic matter. Furthermore, the suspended matter was considered negatively charged. | |||||
Salinity. | |||||
Temperature. In the present study, the temperature is put at 12.5°C, corresponding to the mean air temperature from April till September (the sailing season is typically from the end of April to the beginning of October). | |||||
pH. | |||||
The number of m2 of bottom areas of ships that are in the waters per time unit. | |||||
The percentage of the ships having bottom paint with the examined antifoulant (P). | |||||
Water-holding capacity of the sediment. Apart from a minor content of
organic carbon in the sediment, the composition of the upper sediment layer was assumed to
be identical to the composition of the suspended matter. The sediment was assumed to be
anaerobic. | |||||
Number of boats in the waters in question.
|
Average time which the centre of gravity of the boat stay in the waters:
|
Table B1.1 summarizes the parameters characterizing the two scenarios. These parameters are applied in the basic calculations.
Table B1.1 Look here...
Standard scenario.
2.2 Emission of antifoulants
The rate, at which the antifoulant leaches into the aquatic environment, is expressed as follows:
U = [leached substance per area per time unit].
The measuring of realistic leaching rates of antifoulants is causing great problems as the leaching rate depends on various factors such as:
| The time after painting. The leaching rate has often been demonstrated to decrease as a function of the time as a result of the falling concentration of the substances in the paint. |
| Thickness of the coat of paint |
| Liberation of other substances in the paint |
| Outward circumstances, i.e. whether the boat is sailing or not, currents/water exchange, temperature, etc. The leaching rate is typically higher when the boat is sailing than when it is in port. |
A draft standard (ISO 1999) is available from which the leaching rate can be calculated. The leaching rate is determined on the basis of an estimate of the life of the paint, in which it is simply assumed that all of the antifoulant will be released throughout the life of the paint. The first two weeks after the boat has been painted, a higher leaching rate is anticipated. After two weeks, the leaching rate is considered to be constant. The standard does not take into account that the leaching rate is probably higher while sailing than when the boat is in port, and the standard will thus be likely to overestimate the leaching rate when the boat is in port and underestimate the leaching rate while sailing. Furthermore, the draft standard proposes typical thicknesses of coating and lives of different paints (ISO 1999). On the basis of the proposals of the draft standard on coat thicknesses and lives, the thickness of the coat worn down in six months (corresponding to a sailing season) can be calculated to be 42 mm (soluble matrix), 38 mm (insoluble matrix), 45 mm (tin-based self-polishing paint) and 50 mm (tin-free self-polishing paint). These coat thicknesses are in good agreement with the estimates that Hempel has made, stating an average worn down coat of paint of 42 mm per sailing season for pleasure craft in Denmark (Hempel 1999c). Hempel has based their calculation on the amount of bottom paint sold in the Danish market a year and the number of sailing/motor boats of more than 6 m (corresponding to those painted) and their average bottom area.
In order to simulate the increased leaching rate while sailing, it is assumed that 60 mm of the coat of paint is worn off at constant sailing for 6 months. In order to simulate the lower leaching rate when the boat is in port, it is assumed that 30 mm of the coat of paint is worn off when the boat is constantly in port for 6 months. The above corresponds to the assumption that the boats are sailing for approx. 2 months of a sailing season and are in port for the remaining 4 months and that the leaching rate while sailing is twice the rate when not sailing.
On the basis of confidential information from Hempel on the content of antifoulants, dry matter and density (Hempel 1999b), the average leaching rates for the two types of antifoulants can be calculated. Table B1.2 gives the results of these calculations.
Table B1.2
Calculated average leaching rates.
Antifoulants |
Leaching rate (U) (mg/m2/day) |
|
In port |
While sailing |
|
DCOI |
13 |
25 |
ZPT |
21 |
41 |
In the model, the total leaching of the active substance to the water per time unit is expressed as:
| where | |
| N | is the number of boats being in the water area per day
[boats/day] |
| A | is the average wet bottom area [m2/boat] |
| t | is the time that the centre of gravity of the boats stays in
the waters in question [days] |
| P | is the percentage of the boats that have been painted with the antifoulant in question [%] |
2.3 PEC model
The model is divided into the following parts:
- Mass balance in the water column
- Mass balance in the sediment
Transformation in the water column
The following conditions in the water column were taken into consideration:
| The degradation rate of the parent compound and the subsequent formation of metabolites. Aerobic conditions in the water column were assumed. The effect of the temperature on the degradation rate was included by assuming that the degradation rate is halved when the temperature falls by 10°C (or vice versa). During the modelling period, temperatures are not so low that degradation stops. |
| Abiotic transformation. Degradation of ZPT by photolysis is included. For the two investigated substances, hydrolysis is not considered a significant reaction (cf. Chapters 3 and 4). Like other reactions, degradation by photolysis is temperature dependent but the effect of the temperature is less than for other reactions. Schwarzenbach et al. (1993) thus states that a change in temperature of 10°C only changes the reaction rate by a factor of between 1.15 and 1.5. Therefore, the effect of the temperature on the degradation by photolysis is ignored in the present study. |
| A first order degradation kinetics was assumed for all degradation reactions. |
| No discrimination was made between dissolved substance and substance sorbed to dissolved organic matter (DOC). |
| Sorption to the suspended matter was expressed as a linear adsorption. |
| Linear sedimentation of the suspended matter was assumed. |
| Resuspension of sedimentated matter. In the calculations, the resuspension rate was assumed to be constant. |
The following conditions in the sediment were taken into consideration:
| Sedimentation of suspended matter from the upper water layer. |
| Resuspension of sediment to the upper water layer. |
| A first order anaerobic degradation. The sediment was assumed to be anaerobic for which reason only anaerobic degradation was included. |
| Only the sediment formed during the simulation period was examined. This sediment layer was considered to be a completely homogeneous mixture. |
For both the parent compound and its main metabolites, a mass balance was established for the water column and the sediment.
The following three PECs (Predicted Environmental Concentration) were calculated:
| PEC(water column) | |
| PEC(sediment) | |
| PEC(sediment, pore water) |
These three concentrations were put equal to the steady-state concentration, i.e. the concentration that the calculated concentrations eventually approach when simulating a continuous leaching of the substance to the aquatic environment.
For all substances, the background level is assumed to be 0.
2.4 Data on active substances
2.4.1 DCOI
Aerobic degradation
Figure B1.1 shows the simplified degradation pattern which was assumed for DCOI. At
first, DCOI was assumed to degrade into N-(n-octyl) malonamic acid which, while releasing
CO2, was transformed into N-(n-octyl) acetamide and N-(n-octyl) b hydroxy propionamide. These two metabolites were assumed to be
transformed into a large number of different organic compounds, which were comprised under
"Other metabolites". The half-life of this pseudo-reaction was assumed to be
same as those of N-(n-octyl) acetamide and N-(n-octyl) b
hydroxy propionamide. To a certain degree, these metabolites will be mineralized while
forming CO2 (half-life of this transformation is assumed to be the same for all
"other metabolites").
The half-life of the transformation of DCOI into N-(n-octyl) malonamic acid was determined on the basis of a test in which the removal of DCOI was measured in seawater from the pleasure craft harbour of Jyllinge for a period of 72 hours at 12°C (Jacobson and Kramer 1999). By minimizing the total of the areas of the relative residues of DCOI (RRSQ) stated by Jacobson and Kramer (1999), using the following equation:
| where | ||
| i | is a numeric reference to the observation | |
| yi(observed) | is the measured degradation (%) | |
| yi(estimated) | is the estimated degradation (%) assuming first order kinetics and assuming that yi(estimated) at the time 0 = yi(observed) at the time 0 | |
Half-lives can be calculated to be 12.8 hours (for replicate 1) and 15.3 hours (for replicate 2) with an average half-life of 14.1 hours (at 12°C). The other half-lives were estimated on the basis of the quantities which were considered to be present after 30 days’ aerobic degradation (see Figure B1.1) in experiments carried out by Mazza (1993).
The estimated half-lives of the aerobic transformation of DCOI at 25°C are given in Table B1.3.
Table B1.3 Look here...
Estimated half-lives (days) at 25°C of aerobic degradation of DCOI.
Anaerobic degradation
The anaerobic degradation of DCOI was assumed to follow the same reaction pattern as
the aerobic degradation. The degradation rates were, however, assumed to be slower for the
anaerobic degradation.
The transformation of DCOI at aerobic and anaerobic test conditions is shown as a function of the time in Figure B1.2. Data from Table 3.2 of the main part of this report (aerobic conditions) and from Table 3.4 (anaerobic conditions; concentrations set at 100%). It should be noted that the time axis depicting the anaerobic tests is 4.5 times longer than the time axis of the aerobic tests. Figure B1.2 shows that there is thus a fair correlation between the measured concentrations of the aerobic and anaerobic tests, respectively. In the calculations, it was thus assumed that, under anaerobic conditions, the half-lives of the reactions are 4.5 times longer than under aerobic conditions.
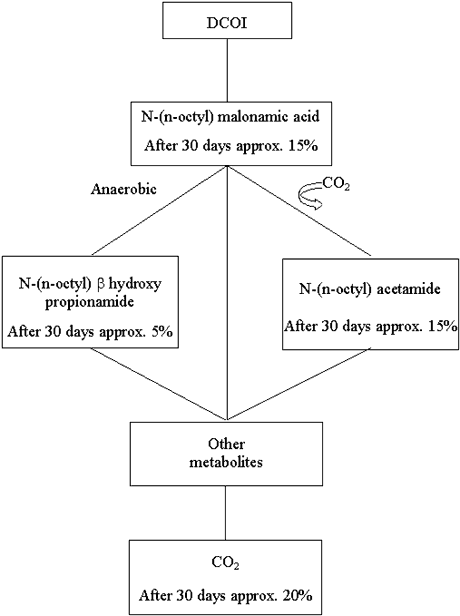
Figure B1.1
Degradation of DCOI.
Figure B1.2 Look here...
Degradation of DCOI under aerobic and anaerobic conditions.
Properties of the substance
Table B1.4 gives selected properties of DCOI and its metabolites. DCOI and the three
metabolites were not assumed to be present in ionized form at pH = 7.
Table B1.4
Properties of DCOI and its metabolites.
Substance |
Molar weight (g/mol) |
Log KOW |
Log KOC |
DCOI |
282 |
2.8** |
3.2 |
N-(n-octyl)malonamic acid |
215 |
2.00* |
1.75* |
N-(n-octyl) b hydroxy propionamide |
201 |
1.77* |
1.789* |
N-(n-octyl) acetamide |
171 |
2.74* |
2.756* |
* Calculated by means of KowWin (Syracuse
Research Corporation 1996).
** Measured (data stated in the main report). Calculated by means of KowWin (Syracuse
Research Corporation 1996).
** Measured (data stated in the main report). * Calculated by means of KowWin (Syracuse
Research Corporation 1996).
** Measured (data stated in the main report).
2.4.2 Zinc pyrithione (ZPT)
Biodegradation
Figure B1.3 shows the simplified biological degradation paths of ZPT which were
simulated in the exposure calculations. It is a very simplified model compared to the very
complicated degradation pathways of ZPT.
The following abbreviations are used:
|
ZPT PT OMDS OMSo PSoA |
Other heterocyclic metabolites with one ring are given as NP1-NP5 (cf. Chapter 4 of the main report). The identity of NP1-NP5 is known to VKI.
Two main degradation paths are assumed:
| 1) | Primarily under aerobic conditions: ZPT ® OMDS ® NP1 ® OMSo + other compounds |
| 2) | Primarily under anaerobic conditions: ZPT® NP3 + OMDS ® NP4 ® PSoA + other compounds |
It was assumed that OMDS, NP3, PSoA and OMSo were further transformed into other compounds, which, to a minor degree, are mineralized.
The half-life of the primary reaction (ZPT ® PT-® OMDS + NP3) was set at 0.5 days. The other half-lives were estimated on the basis of the quantities found in the aerobic and anaerobic degradation tests in which the concentrations of substance were measured as a function of the time (these tests are discussed in the main report).
The estimated half-lives of the aerobic and anaerobic degradation are given in Tables B1.5 and B1.6. Measured and calculated concentrations are depicted in Figure B1.4.
Table B1.5
Model simulation of aerobic biodegradation of zinc pyrithione. Estimated half-lives
(days) at 25°C.
Parent compound |
Metabolites |
|||||||
ZPT |
OMDS |
NP4 |
PSoA |
NP1 |
OMSo |
Other |
CO2 |
|
ZPT |
- |
0.5 |
- |
- |
- |
- |
- |
- |
NP3 |
- |
- |
- |
- |
- |
- |
50 |
- |
OMDS |
- |
- |
4.0 |
- |
2.0 |
- |
4.0 |
- |
NP4 |
- |
- |
- |
15.0 |
- |
- |
- |
- |
PSoA |
- |
- |
- |
- |
- |
- |
250 |
- |
NP1 |
- |
- |
- |
- |
- |
15.0 |
- |
- |
OMSo |
- |
- |
- |
- |
- |
- |
80 |
- |
Other compounds |
- |
- |
- |
- |
- |
- |
- |
2,000 |
CO2 |
- |
- |
- |
- |
- |
- |
- |
- |
Table B1.6
Model simulation of anaerobic biodegradation of zinc pyrithione. Estimated half-lives
(days) at 25°C.
Parent compound |
Metabolites |
||||||||
ZPT |
NP3 |
OMDS |
NP4 |
PSoA |
NP1 |
OMSo |
Other |
CO2 |
|
ZPT |
- |
0.5 |
30 |
- |
- |
- |
- |
- |
- |
NP3 |
- |
- |
- |
50 |
- |
- |
- |
50 |
- |
OMDS |
- |
- |
- |
4.0 |
- |
2.0 |
- |
4.0 |
- |
NP4 |
- |
- |
- |
- |
15.0 |
- |
- |
- |
- |
PSoA |
- |
- |
- |
- |
- |
- |
- |
5.0 |
- |
NP1 |
- |
- |
- |
- |
- |
- |
15.0 |
- |
- |
OMSo |
- |
- |
- |
- |
- |
- |
- |
80 |
- |
Other compounds |
- |
- |
- |
- |
- |
- |
- |
- |
6,000 |
CO2 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
Photolysis
As mentioned above, the degradation of ZPT by photolysis is included in the model
simulations. ZPT is assumed to be transformed into NP3 in the photolytical degradation.
In daylight about noon, the photolytical half-life of ZPT was estimated at:
| 1.78 min without cloud cover | |
| 3.74 min with cloud cover |
The tests were made in September on the parallel approx. 42°N, where the degradation rate of ZPT in seawater was followed (Fenn 1999). The tests were made in curved tubes. A first order rate constant kP can be estimated to be 0.18 min-1 (without cloud cover) and 0.08 min-1 (with cloud cover). A factor of 2.2 was used in order to correct for the curving of the tubes.
At a cloudless sky, it is assumed that the measured photolytical rate constant may be described by (cf. Schwarzenbach et al. 1993):
| where | |
| F | is the so-called quantum yield, which is here assumed to be independent of the wavelength [-]. F states the amount of molecules exited by the light that are transformed into another compound. |
| is the specific rate of light absorption [time-1]. This rate was calculated by (Schwarzenbach et al. 1993): |
|
| l | is wavelength [nm]. |
| W(l) | is the light intensity at various wavelengths [milliEinstein/cm2/time/nm]. The light intensity in the autumn on the parallel 40°N was borrowed from Zepp and Cline (1977). |
| D(l) | is the ratio of the average length of the trajectory of the light to the depth of a water element, which can be assumed to be completely mixed [-]. D(l ) is here as- sumed to be equal to 1 for all wavelengths. |
| e(l) | is the so-called molar extinction coefficient [(mol/l- 1/cm]. For ZPT, these values are borrowed from Fenn (1999). |
The light deflection of the cuvette has been taken into consideration.
F was thus determined to be 0.07.
Then the American program GCSOLAR (U.S. EPA 1999) was used for calculating the photolytical half-life. This program uses the so-called attenuation coefficients, a1, which are applied in order to calculate to which degree the water absorbs the light as a function of the depth.
The attenuation coefficient for the water at Kronprins Frederiks Bro is determined on the basis of measured Secchi disk transparencies at two stations in the vicinity of the bridge (Counties of Roskilde and Frederiksborg 1997). In the summer, the shortest Secchi disk transparency is approx. 2.5 m. By using data from Calkins (1977), the following correlation between the Secchi disk transparency and the attenuation coefficient a was found at Secchi disk transparencies of less than 4 m:
a [m-1] = 3.05 - 0.57 × Secchi disk transparency [m].
The attenuation coefficient for the pleasure craft harbour of Jyllinge was found on the basis of literature data on coastal areas (Zafirioiu 1977). The values are here stated as a function of wavelength and with a minimum and a maximum value. The highest values are used in the present calculations.
GCSOLAR does not take the effect of the cloud cover on the photolysis rate into account. The American program EXAMS (Burns et al. 1981), which can also be used for simulating the photolysis of substance, does, however, take the effect of the cloud cover on the photolysis rate into account. By using EXAMS, it was estimated that, compared to the half-life at a blue sky, the half-life will be approx. 50% higher at a cloud cover of 60% which is the average cloud cover in Denmark from April to September (Danish Statistical Office 1996).
GCSOLAR can calculate the average photolytical half-life for each of the seasons: Spring, summer, autumn and winter and on various lattitudes (however, only lattitudes divisible by 10). The average photolytical half-life of ZPT for the seasons spring, summer and autumn and on the lattitudes 50° and 60° was found to be 9.8 hours for the pleasure craft harbour of Jyllinge (6.5 hours at blue sky) and 6.6 hours for the narrows at Kronprins Frederiks Bro (4.4 hours at blue sky).
The degradation by photolysis is slightly dependent on the temperature. A dependency of the photolytical degradation on temperature is, however, not included in the present calculations.
The photolytical half-life was determined for open waters where cloud cover and the falling light intensity down through the water column are taken into consideration but where the boats in the harbour and the shadow effects of the pier are not taken into account. Therefore, two types of calculations have been made, one in which the degradation by photolysis is taken into account and another in which the photolytical degradation is ignored. The actual conditions will probably be somewhere between these two reflections but it is not possible right away to quantify the importance of the shadow effect of the boats and the pier on the amount of light actually falling on the water surface. For the busy navigation route under the bridge (Kronprins Frederiks Bro), there will be limited admittance of sunlight right under the bridge while there will be no important shadow effects in the other part of the navigation route.
Properties of the substance
The properties of zinc pyrithione and its metabolites are summarized in Table B1.7.
The different heterocyclic metabolites with one ring have a low calculated log KOW, which indicates a high water solubility. The sulfonic acids are also expected to be very strong acids for which reason they are probably fully ionized at the prevailing pH in the two waters. For these two compounds, the sorption to sediment and suspended matter is thus expected to be low. The calculated KOC values are, however, used for estimating the sorption to suspended matter and to the sediment.
Table B1.7
Properties of zinc pyrithione and its metabolites.
Substance |
LogKOW |
LogKOC |
ZPT |
0.97** |
2.9-4.0 |
NP3 |
1.50* |
1.728* |
OMDS |
-2.35* |
3.355* |
NP4 |
-2.36* |
0.912* |
PSoA |
-2.35* |
1.072* |
NP1 |
-4.50* |
1.131* |
OMSo |
-4.49* |
1.291* |
Other compounds |
-3.0*** |
1.1*** |
| * | Calculated by means of KowWin (Syracuse Research Corporation 1996). |
| ** | Measured (data stated in the main report). |
| *** | Fictive |
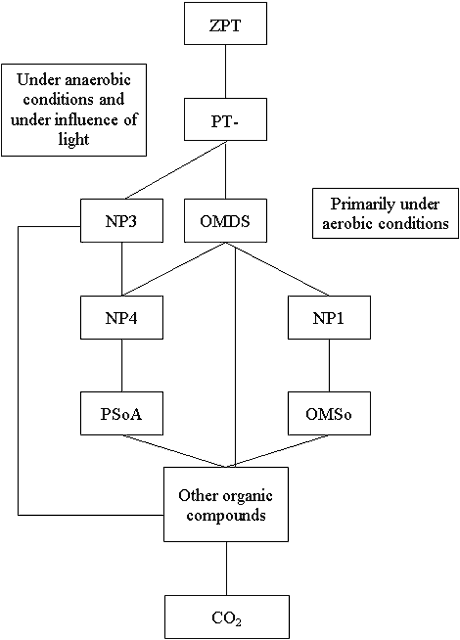
Figure B1.3
Aerobic and anaerobic degradation of zinc pyrithione.
Figure B1.4a Look here...
Calculated and measured concentrations of zinc pyrithione
and its metabolites. Aerobic experimental conditions.
Figure B1.4b Look here...
Calculated and measured concentrations of zinc pyrithione
and its metabolites. Anaerobic experimental conditions.
3. Calculation results
Table B1.8 gives the calculated PEC values for the two scenarios and the various substances. As mentioned above, the concentrations are steady-state concentrations.
It appears from Table B1.8 that the highest calculated concentrations were found for the pleasure craft harbour. Here, the calculated concentrations are approx. 100 times higher than the concentrations calculated for the busy navigation route.
For the parent compounds, the following steady-state concentrations for the water phase, PEC(water), were estimated:
| • | DCOI: | 0.52 mg/L | (pleasure craft harbour) |
| 0.006 mg/L | (busy navigation route) | ||
| • | Zinc pyrithione: | 0.56 mg/L | (pleasure craft harbour, photolysis included) |
| 1.7 mg/L | (pleasure craft harbour, photolysis not included) | ||
| 0.005 mg/L | (busy navigation route, photolysis included) | ||
| 0.022 mg/L | (busy navigation route, photolysis not included) |
Table B1.8a Look here...
Calculation results of DCOI.
Table B1.8b Look here...
Calculation results of ZPT.
4. Sensitivity analysis
The calculation results are conditional on i.a. the values assigned to the different parameters.
A sensitivity analysis of the effect of the following parameters on the calculated concentrations of the parent compounds (DCOI and ZPT) was made:
| Harbour scenarios. Supplementary PEC calculations were made for five pleasure craft harbours (cf. Section 4.1 below). |
| Temperature. The temperature was varied between 5°C and 15°C as this was considered a typical variation in the temperatures for the months from May till September (cf. Section 4.2 below). |
| Water exchange. The water exchange was varied between 0 m3/m2/d corresponding to no water exchange and 1 m3/m2/d which would occur under specific conditions (cf. Section 4.2 below). | |
| Sedimentation rate. The sedimentation rate was varied between 0.7 m/d, corresponding to the net sedimentation being almost 0, and up to 1.5 m/d (cf. Section 4.2 below). |
| Leaching rate. The total leaching rate was varied between 50% and 200% of the total leaching rate used in the basic calculations (cf. Section 4.2 below). |
4.1 Harbour scenarios
Supplementary calculations were made for five other pleasure craft harbours. A characterization of these harbours is given in Table B1.9. These data were obtained by Hempel and passed on to VKI.
The water exchange in the harbours was set at 0.6 m3/m2/day for all harbours with the exception of the harbours of Svendborg and Horsens. For the pleasure craft harbour of Horsens, the water exchange was set at 0.8 m3/m2/day. The pleasure craft harbour of Svendborg is a pile-built harbour in Svendborg Sund. Therefore, the flow conditions are assumed to correspond to those of Svendborg Sund. An average flow rate of 0.5 m/s was assumed for the pleasure craft harbour of Svendborg corresponding to the amplitude of the drastic periodic velocity variation caused by the tides in Svendborg Sund (Harremoës and Malmgren-Hansen 1989).
Table B1.9 Look here...
Harbour scenario (prepared by Hempel).
Note: Difference of height is used as a parameter in stead of tides. As the tidal variation in Denmark is very small (10-40 cm), the primary water exchange is made by wind and currents. Therefore, the difference in height is an overall assessment of the different parameters.
Information was obtained from (conversations with):
Jyllinge: Steen Wintlev DS + map received
Grenå: Benny Andersen
Svendborg: Kurt Hansen
Rungsted: Finn Rosdahl
Horsens: Hilmer Christoffersen
Egå Marina: Dan Nilsson (harbour master Børge Heilbach)
The calculated steady-state concentrations for these harbour scenarios are given in Table 1.10.
Table B1.10
Calculated steady-state concentrations.
Harbour |
Number of boats per harbour volume in relation to number of boats per harbour volume in the pleasure craft harbour of Jyllinge |
PEC(water) (mg/L) |
PEC(water) (DCOI) (mg/L) |
|
| With photolysis |
Without photolysis |
|||
Jyllinge |
1.0 |
0.56 |
1.70 |
0.52 |
Grenå |
0.2 |
0.11 |
0.28 |
0.08 |
Horsens |
0.7 |
0.49 |
1.14 |
0.35 |
Rungsted |
0.3 |
0.02 |
0.08 |
0.02 |
Egå Marina |
0.5 |
0.29 |
0.81 |
0.25 |
Svendborg |
0.5 |
<0.01 |
<0.01 |
<0.01 |
Table B1.10 indicates that the pleasure craft harbour of Jyllinge results in the highest calculated concentrations. The main reason for this is that there are relatively more boats in the pleasure craft harbour of Jyllinge compared to the volume of water needed in order to dilute the leached chemical (Table B1.10). The scenario used is thus a conservative scenario as assumed at the selection of the pleasure craft harbour of Jyllinge.
4.2 Sensitivity analysis of other parameters
Tables B1.11a and B1.11b show the relation between the calculated concentration of the parent compound in the water phase after changing the parameter and the calculated concentration of the standard scenario.
Tables B1.11a and B1.11b indicate that, within the variation assigned to the individual parameters, it is the total leaching rate that causes the largest variations in the calculated concentrations. The sedimentation rate only slightly influences the calculated concentrations of the parent compounds.
Table B1.11a
Sensitivity analysis of PEC(water) of DCOI. The figures indicate the relation between
the calculated concentration of the parent compound in the water phase, after changing the
parameter, and the calculated concentration in the standard scenario.
Parameter |
Pleasure craft harbour of Jyllinge |
|
PEC(water) |
PEC(water) |
|
Standard scenario |
1.0 |
1.0 |
Temperature 5°C |
1.5 |
1.6 |
Temperature 15°C |
0.9 |
0.9 |
No water exchange |
1.2 |
1.1 |
167% increased water exchange |
0.9 |
0.9 |
70% lower sedimentation rate |
1.0 |
1.0 |
150% higher sedimentation rate |
1.0 |
1.0 |
50% less leaching |
0.5 |
0.5 |
200% more leaching |
2.0 |
2.0 |
Table B1.11b
Sensitivity analysis of PEC(water) of ZPT. The figures indicate the relation between
the calculated concentration of the parent compound in the water phase, after changing the
parameter, and the calculated concentration in the standard scenario.
Scenario |
Parameter |
With |
Without |
PEC(water) |
PEC(water) |
||
Pleasure craft harbour of Jyllinge |
Standard scenario |
1.0 |
1.0 |
Temperature 5°C |
1.1 |
1.4 |
|
Temperature 15°C |
1.0 |
0.6 |
|
No water exchange |
1.1 |
1.6 |
|
167% increased water exchange |
0.9 |
0.6 |
|
70% lower sedimentation rate |
1.0 |
1.2 |
|
150% higher sedimentation rate |
1.0 |
1.0 |
|
50% less leaching |
0.5 |
0.5 |
|
200% more leaching |
2.0 |
4.0 |
|
| Busy navigation route | Standard scenario | 1.0 | 1.0 |
| Temperature 5°C | 1.2 | 1.5 | |
| Temperature 15°C | 0.9 | 0.9 | |
| No water exchange | 1.1 | 1.2 | |
| 167% increased water exchange | 0.9 | 0.9 | |
| 70% lower sedimentation rate | 1.0 | 1.0 | |
| 150% higher sedimentation rate | 1.0 | 1.0 | |
| 50% less leaching | 0.5 | 0.5 | |
| 200% more leaching | 2.0 | 2.0 |
_______________
1) If the light intensity at the surface is expressed as
I0 and the light intensity in the depth z as I, the correlation between I and I0
is described as log10(I/I0) = -a × z
Back...
[Front page] [Contents] [Previous] [Next] [Top] |