8 Statistisk model

Udvikling af en metode til effektvurdering af Miljøstyrelsens Kemikalieinspektions tilsyn og kontrol

Formålet med formuleringen af en statistisk model er at kunne beskrive det samlede antal ulovlige produkter ud fra

et estimat for det samlede antal produkter på markedet
antallet af ulovlige produkter fundet ved stikprøve.

Vi vil først præsentere en generel tilgang til statistisk modellering. Derefter vil vi beskrive en simpel model med to sandsynlighedsfordelinger, som kan udvides til en stratificeret model.

8.1 Generelt

Udgangspunktet for den statistiske analyse er et sæt af observationer. Dette kunne fx være resultatet af en undersøgelse af et antal legetøjsprodukter for indhold af ftalater. Hvis observationen er givet ved {0, 0, 0, 1, 0, 0, 0, 1, 1, 0}, betyder det, at det fjerde, det ottende og det niende produkt havde udfaldet ”succes” (hér: indhold af ftalater, dvs. ulovligt produkt).

Vi vil i almindelighed bare tale om én observation, selv om det kan dreje sig om mange målinger. En observation er således en vektor x=(x₁,...,x_n) af tal. Observationen antages formelt at være en realisation af en stokastisk variabel X=(X₁,...,X_n). X’s værdier tilhører udfaldsrummet E, mængden af mulige udfald.

Idéen med at indføre den stokastiske variabel X er, at vi sammen med vores observation X betragter alle de andre udfald, vi kunne have fået. Ved hjælp af den statistiske model prøver vi så at beskrive usikkerheden omkring udfaldet ved en eller flere sandsynlighedsfordelinger. Ofte har man et vist kendskab til fordelingen for X. Måske ved man, at X’s fordeling er en binomialfordeling, men ved ikke hvad sandsynlighedsparameteren er. På grundlag af en eller flere observationer vil vi så prøve at skønne over, hvilken binomialfordeling der er den rigtige. Det, vi kalder den statistiske model, er mængden af de mulige sandsynlighedsfordelinger. For at holde rede på dem indicerer man dem. Dette sker så vidt muligt på en naturlig måde. En sådan mængde af sandsynligheder plejer man i statistikken at kalde en familie af sandsynligheder.

Formelt siger vi, at en statistisk model er en indiceret familie (Ρ_θ)_θεΘ af sandsynlighedsfordelinger på E, således at for hvert θ er Ρ_θ en mulig fordeling af X. Indeksmængden Θ kaldes parameterområdet, og θ kaldes parameteren.

At vælge en fordeling på grundlag af observationen X kaldes at estimere. Man plejer her at identificere fordelingen Ρ_θ med dens parameter θ og taler så om at estimere parameteren θ. Hvis man ved 100 kast med en skummel og skævt udseende mønt har fået krone 33 gange og bliver bedt om at give et skøn over, hvad sandsynligheden for krone ρ er, vil det være nærliggende at vælge ρ=0,33, hvis man i øvrigt ikke ved noget om mønten. Estimation betyder altså, at vi ud fra observationen x prøver at bestemme den fordeling, som vi tror x kommer fra. Ser vi igen på binomialfordelingen, er der selvfølgelig ingen grund til at tro, at ρ netop er 0,33, men nok at ρ ligger nær 0,33. Havde udsagnet været baseret på 330 kroner ud af 1.000 kast, ville man nok have været mere overbevist om, at 0,33 kunne være det rigtige.

Der findes mange forskellige estimeringsmetoder, dvs. forskrifter, der fortæller, hvordan man i en given model vælger en fordeling på grundlag af et sæt af observationer. En sådan forskrift, der altså er en funktion af observationerne, kaldes en estimator. Vi vil holde os til den såkaldte maksimaliseringsmetode. Denne metode giver i almindelighed fornuftige estimatorer.

Det engelske ord for maksimaliseringsestimator er maximum likelihood estimator. Derfor bruges forkortelsen ML-estimator ofte for maksimaliseringsestimatoren.

Hvis X er binomialfordelt, dvs. , da er maksimaliseringsestimatoren for sandsynligheden ρ entydigt bestemt og givet ved

8.2 Simpel model

Vi vil tage udgangspunkt i en model uden stratifikation. Vi betragter således populationen af produkter som en helhed uden underopdeling.

Til at beskrive antallet af ulovlige produkter i populationen vil vi anvende to sandsynlighedsfordelinger: binomialfordelingen og normalfordelingen. Vi antager, at antallet af ulovlige produkter er binomialfordelt med antalsparameter og sandsynlighedsparameter ρ , og vi antager, at antalsparameteren er normalfordelt med middelværdi µ og varians σ². Idet antalsparameteren i binomialfordelingen skal være et naturligt tal, vil vi i praksis anvende afrundede værdier af normalfordelingen. Den statistiske betydning af at anvende afrundede værdier er i denne sammenhæng bagatelagtig.

Formelt har vi:

I forbindelse med stikprøveudtagning betegnes antallet af observationer i stikprøven π og antallet af ”succeser” (ulovlige produkter) υ.

Notationen kan illustreres i nedenstående figur:

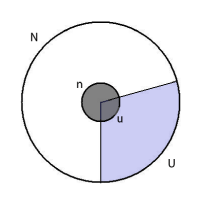
Den yderste cirkel repræsenterer hele markedet, og den inderste mørke cirkel repræsenterer den udtagne stikprøve. Idet andelen af ulovlige produkter i stikprøven (u/n) antages at svare til andelen af ulovlige produkter på hele markedet (U/N), kan U bestemmes ud fra N, n og u.

I appendiks er de væsentligste statistiske egenskaber for udledt, og det fremgår, at middelværdi og varians af den stokastiske variabel er givet ved:

Eksempel I (simpel model):

Vi forventer, at det samlede antal produkter på markedet er 10.000 med standardafvigelse på 15 % (dvs. med 95 procents konfidens forventes det, at antallet af produkter tilhører intervallet [7000,13000], svarende til 10000 ± 2 · 1500). Vi udtager en stikprøve på 50 produkter. Lad stikprøvens resultat være 15 ulovlige produkter. Vi har således n=50 og u=15. ML-estimatet for sandsynlighedsparameteren i binomialfordelingen baseret på vores observation (stikprøve) vil være , og på den baggrund vil vi skønne, at der er 10000 · 0,3=3000 ulovlige produkter på markedet. Men usikkerheden af vores skøn vil afhænge, dels af variansen på vores estimat af det samlede antal produkter på markedet (givet ved σ² =1500²), og dels af variansen af vores estimat for ”succes”-sandsynligheden (givet ved ρ²=ρ(1-ρ)/n=0,0042). Den samlede usikkerhed af vores skøn er givet ved standardafvigelsen for , der i dette eksempel udgør svarende til 26,5 %. Konklusionen er således, at det forventede antal ulovlige produkter på markedet med 95 procents konfidens tilhører intervallet [1410,4590], svarende til 3000 ± 2 · 795.

8.3 Model med stratifikation

Formålet med at indføre stratifikation i modellen er at reducere usikkerheden (målt ved standardafvigelsen) på estimatet af antallet af ulovlige produkter. Stratifikation er således et middel til at optimere udnyttelsen af ressourcer i forbindelse med stikprøveudtagning.

Den simple model, der blev beskrevet i forrige afsnit, udvides nu til også at omfatte stratifikation, dvs. at populationen af produkter underopdeles i lag (strata).

Vi vil stadig anvende binomialfordelingen og normalfordelingen til at beskrive antallet af ulovlige produkter i populationen, men nu antager vi, at populationen er inddelt i k uafhængige strata. Vi antager, at antallet af ulovlige produkter i det i’te strata er binomialfordelt med antalsparameter og sandsynlighedsparameter ρ_i, og vi antager, at antalsparameteren er normalfordelt med middelværdi µ_i og varians σ_i².

I forhold til Kemikalieinspektionens nuværende tilgang er det ”nye”, at der skal estimeres (antages) en varians/standardafvigelse af populationernes størrelse i de enkelte strata.

Formelt har vi:

Og antallet af ulovlige produkter i hele populationen fås ved at summere over alle strata:

8.4 Stikprøvestørrelse i model med stratifikation

Til at bestemme de optimale stikprøvestørrelser i en stratificeret model anvender vi Neymans allokeringsmetode^[4]. Metoden giver en optimal stikprøveallokering baseret på middelværdier og standardafvigelser i de enkelte strata.

Lad n_i^* betegne den optimale stikprøvestørrelse fra det i’te strata:

Antallet af stikprøver fra de enkelte strata kan illustreres i nedenstående figur:

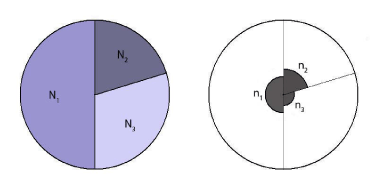
Cirklen i venstre side repræsenterer beskrivelsen af hele populationen, hvor farven, hørende til de enkelte strata, er en illustration af variansen (jo større varians desto mørkere farve). Cirklen i højre side repræsenterer stikprøven baseret på Neymans allokeringsmetode. Det ses af figuren, at metoden medfører, at der udtages relativt flest stikprøver fra strata med størst varians.

Hvis antallet af stikprøver fra den samlede population er givet, så er den optimale allokering af stikprøvestørrelser fra de enkelte strata entydigt givet ud fra middelværdier og standardafvigelser i de k forskellige normalfordelinger, der beskriver det samlede antal produkter i hvert stratum.

8.5 Analyse af stikprøve

På baggrund af resultatet af stikprøverne kan den ”mest sandsynlige” frekvens af ulovlige produkter bestemmes for hvert stratum, hér anvendes ML-estimatoren, der i sig selv er en stokastisk variabel med en standardafvigelse, der afhænger af u og n.

Næste skridt er at kombinere stikprøveanalysen med estimatet for det samlede antal produkter.

Formelt haves nu for alle strata:

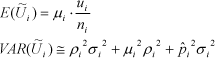
Formel

Alle resultater i modellen bygger på den antagelse, at de normalfordelinger, der beskriver den samlede population i de enkelte strata, er uafhængige. Der kan argumenteres for, at der vil være tendens til, at man enten konsekvent over- eller undervurderer middelværdi og varians i de forskellige strata, og at fordelingerne dermed ikke er uafhængige. Hvis uafhængighedsantagelsen ikke holder, vil den stratificerede model undervurdere usikkerheden, og det er på den baggrund afgørende for den statistiske models relevans at sikre, at de normalfordelinger, som beskriver de enkelte strata, er uafhængige.

8.6 Statistisk konklusion

Der er umiddelbart tre typer af konklusioner, som kan foretages på baggrund af den statistiske model.

På baggrund af estimatet for det samlede antal produkter på markedet og den udtagne stikprøve kan MST med {konfidensniveau} procents sikkerhed sige, at antallet af ulovlige produkter på markedet udgør mellem {min} og {max}.
På baggrund af estimatet for det samlede antal produkter på markedet og den udtagne stikprøve kan MST med {konfidensniveau} procents sikkerhed sige, at antallet af ulovlige produkter på markedet udgør mindst {min}.
På baggrund af estimatet for det samlede antal produkter på markedet og den udtagne stikprøve kan MST med {konfidensniveau} procents sikkerhed sige, at antallet af ulovlige produkter på markedet udgør højst {max}.

Konklusion 1 er tosidet, mens konklusion 2 og 3 er ensidede. Der gælder følgende sammenhæng:

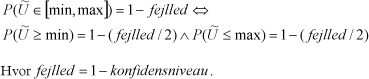
Formel

8.7 Samlet fremgangsmåde

Den samlede fremgangsmåde i forbindelse med planlægning, udtagning, analyse og konklusion af stikprøver kan opsummeres i følgende punkter:

Eksempel II (stratificeret model):
Lad igen estimatet for det samlede antal produkter på markedet være givet ved 10.000, men nu er markedet underopdelt i tre uafhængige strata. For hvert stratum skal der estimeres middelværdi og varians/standardafvigelse. Lad disse være givet ved følgende tabel:


Stratum, i	1	2	3
Middelværdi, µ_i	5.000	3.000	2.000
Standardafvigelse, σ_i	10 %	15 %	27,5 %

Bemærk, at det vægtede gennemsnit af de anvendte standardafvigelser er

15 %, dvs. lig med standardafvigelsen i eksempel I. Det skal dog vise sig, at standardafvigelsen af det samlede antal produkter på markedet i dette eksempel kun udgør 8,7 %! Der gælder nemlig, at standardafvigelsen omkring summen af uafhængige normalfordelte variable er mindre end summen af standardafvigelserne på de enkelte variable.

Vi udtager igen i alt 50 produkter, men denne gang underopdeles stikprøven i tre del-stikprøver. For at minimere den forventede varians af det samlede estimat anvendes Neymans allokeringsmetode, der medfører, at der skal udtages stikprøver fra det første stratum. Tilsvarende beregninger gennemføres for det andet og tredje stratum.

Lad resultatet af stikprøverne være givet ved følgende tabel:


Stratum, i	1	2	3
Stikprøve, n_i	25	14	11
Ulovlige, µ_i	8	4	3

Vi kan nu beregne ML-estimaterne for ’erne, der sammenholdt med

µ_i’erne giver os de forventede værdier af det samlede antal ulovlige produkter i hvert stratum. For det første stratum forventes således ulovlige produkter. Vi kan også beregne -estimatorernes standardafvigelser ρ_i. For det første stratum fås således:

Ved at sammenholde standardafvigelserne på ’erne med standardafvigelserne på ’erne kan vi beregne standardafvigelserne på estimatet af det samlede antal ulovlige produkter i det i’te stratum. Lad τ_i betegne standardafvigelsen på . Vi har således:


Stratum, i	1	2	3
Middelværdi,	1.584	880	540
Standardafvigelse, τ_i	491	397	314
Varians	491²	397²	314²

Næste skridt i analysen er at konsolidere resultaterne fra de enkelte strata til den samlede population. Vi udnytter, at variansen af uafhængige normalfordelinger er ”additiv”, dvs. at summen af varianserne er lig med variansen af summen. Vi får således, at variansen af , dvs. det samlede antal ulovlige produkter i hele populationen er lig med 491² + 397² + 314²= 491624, og standardafvigelsen af det samlede antal ulovlige produkter i hele populationen er dermed givet ved:

Det kan ses, at denne standardafvigelse er 12 % mindre end den tilsvarende standardafvigelse i eksempel I. Reduktionen skyldes, at en del af variationen, der er inden for de enkelte strata, ”udjævnes”, når man betragter hele populationen.

Med middelværdi og standardafvigelse på plads kan vi foretage statistiske konklusioner på baggrund af forskellige konfidensniveauer. I tabellen nedenfor er konfidensintervallerne angivet for en række ofte anvendte konfidensniveauer.


	Konfidensinterval
Konfidensniveau	Nedre grænse	Forventet værdi	Øvre grænse
80 %	2.414	3.004	3.594
90 %	2.105	3.004	3.903
95 %	1.851	3.004	4.157
97,5 %	1.630	3.004	4.378

Ved anvendelse af 95 procents konfidens ses det, at konfidensintervallet udgør [1851,4157], dvs. at på baggrund af estimatet for det samlede antal produkter på markedet og den udtagne stikprøve kan vi med 95 procents sikkerhed sige, at antallet af ulovlige produkter på markedet udgør mellem 1851 og 4157.

8.8 Excel-værktøj

Den statistiske model er blevet implementeret i et Excel-regneark. Der er tale om en prototype, der primært skal illustrere de muligheder, som en it-løsning kan levere.

I første omgang leverer regnearket den optimale allokering af del-stikprøver på baggrund af en række input om den samlede population og stikprøvestørrelse. På baggrund af faktiske stikprøveresultater leverer regnearket middelværdi og standardafvigelse af den stokastiske variabel, der beskriver det samlede antal ulovlige produkter. I et særskilt faneblad ”oversættes” resultaterne vedrørende middelværdi og standardafvigelse til konfidensintervaller ved anvendelse af forskellige konfidensniveauer.

Herunder er indsat eksempler på skærmbilleder fra Excel-modellens to nuværende faneblade:

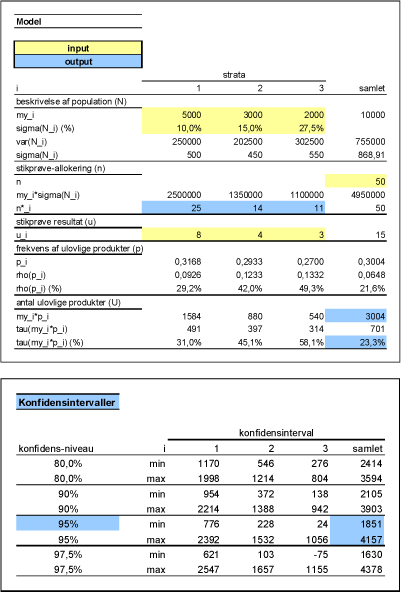
Det anbefales, at regnearket eller en tilsvarende løsning løbende udbygges og kvalitetssikres. I den forbindelse vurderes det, at følgende elementer kunne være relevante at modellere yderligere:

Sammenhæng mellem stikprøvestørrelser og omkostninger. Hvis modellen udvides med oplysninger om stikprøveomkostninger i de forskellige strata, så vil modellen kunne påbegynde at levere ”cost/benefit”-input til planlægningen af stikprøveudtagning.
Sammenhæng mellem stikprøvestørrelser og konfidens. Modellen vil forholdsvis let kunne udvides til at omfatte en funktion, der kan optimere stikprøvestørrelser i forhold til givne konfidensniveauer.
Sammenligning af kampagner. Det vil kunne være relevant at foretage opfølgning på tidligere udførte kampagner for eksempelvis at vurdere eventuelt ændret adfærd i de tilsynsbelagte virksomheder. I den forbindelse vil deciderede hypotesetest være et relevant værktøj.

En fuldt udbygget model vil således samlet kunne vurdere stikprøvestørrelser (fordelt på strata), konfidens af resultater og omkostninger forbundet med udtagelsen. Disse input kan i sammenhæng med den overordnede segmentering (beskrevet i afsnit 5, ”Målretning af tilsyn og kontrol”, side 17) give værdifuldt input til udvælgelse og prioritering af Kemikalieinspektionens fremtidige kampagner.

[4] J. Neyman: ”On two different aspects of the representative method: the method of stratified sampling and the method of purposive selection,” J. R. Statist. Soc. 97 (1934), 558-606.