Projektet med titlen ”Udvikling af en metode til effektvurdering af Miljøstyrelsens Kemikalieinspektions tilsyn og kontrol” er gennemført af PricewaterhouseCoopers (PwC) på opdrag fra Miljøstyrelsen (MST) i perioden oktober 2008 til april 2009.

Det har været projektets overordnede formål at udvikle en stabil, robust og gennemskuelig metode til at opgøre effekten af Kemikalieinspektionens tilsyn og kontrol.

MST har sammenfattet projektets formål i følgende hovedpunkter:

Analyse af den nuværende metodik for tilsyn og kontrol med henblik på videreudvikling af tilgangen og implementeringen af en statistisk metode.
Dokumentation af en statistisk metode, der kan opgøre antallet af ulovlige produkter på det danske marked, baseret på
1. et estimat for det samlede antal forbrugerprodukter
2. en metodik for udtagelse af stikprøver og vurdering af antallet af prøver, der ikke overholder gældende regler.
Oplæg til samlet framework for stikprøvemetodik, dataindsamling, effektberegning og rapportering, herunder vurdering af omkostninger og risici.

En følgegruppe bestående af repræsentanter fra MST og PwC har haft til opgave at vurdere projektets planlægning, forløb og resultater.

Rapporten er udarbejdet af PwC på baggrund af møder med MST’s Kemikalieinspektion og udleveret materiale.

Projektet blev færdiggjort med afleveringen af denne rapport 14. april 2009.

Efterfølgende har PwC redigeret afsnittet ”executive summary” på baggrund af input fra MST. Denne endelige udgave forelå 10. juli 2009.

2 Executive summary

Det har været projektets overordnede formål at udvikle en stabil, robust og gennemskuelig metode til at opgøre effekten af Kemikalieinspektionens tilsyn og kontrol.

Der findes ikke på nuværende tidspunkt en struktureret metode for opsamling af data. Der findes dog megen information gemt i rapporter, årsberetninger og kortlægninger, som vil kunne bruges i en statistisk model.

For fremtidig dataindsamling foreslås det, at der oprettes en database, hvor al relevant information samles på et sted i struktureret form.

Der findes på nuværende tidspunkt ikke en konsistent proces til at vurdere antallet af ulovlige produkter på baggrund af et estimat for det totale antal produkter. Der vil i nogle tilfælde af implementering af en model være behov for indsamling af data, specielt omkring det totale antal produkter.

Nedenstående figur illustrerer de individuelle elementer i en fremtidig samlet løsning:

Formålet med formuleringen af en statistisk model er at kunne beskrive det samlede antal ulovlige produkter ud fra:

Et estimat for det samlede antal produkter på markedet
Antallet af ulovlige produkter fundet ved stikprøve.

En stabil model kræver ensartede og konsistente processer omkring dataindsamling og modellering. I forhold til indsamlingen af information foreslås det, at der oprettes en database med information omkring de enkelte segmenter for at kunne opbygge et ”landkort” over markedet. I første omgang vil fokus være på en segmentering af markedet. Fremadrettet skal der opsamles information om antallet af ulovlige produkter (er dog også en mulig segmenteringsvariabel) og totale antal produkter.

Der findes i dag information fra allerede gennemførte kampagner, som dog skal struktureres. Der findes mange muligheder for indhentning af information, som allerede er brugt hos MST i dag. Der kan eventuelt suppleres med nye datakilder enten i form af andre dataudbydere, spørgeskemaundersøgelser faciliteret af MST eller direkte spørgsmål til virksomhederne under kampagnerne. Specielt for det samlede antal produkter skal der lægges ressourcer, da der ikke findes en indsamlingsproces i dag.

På kort sigt kan implementeringen af den statistiske model underbygge og dokumentere den nuværende tilgang til udtagning og analyse af stikprøver.

På lidt længere sigt kan udviklingen af en metode, hvor der er sammenhæng mellem omkostninger og diverse beslutningsvariable, fx hvilke områder skal udvælges til kampagner? Hvor mange stikprøver skal udtages i hver kampagne? Hvilket statistisk konfidensniveau skal anvendes? Hvor mange kampagner kan/skal gennemføres årligt?

Det er rapportens vurdering, at en model, der både inddrager dataindsamling, stikprøveudtagelse, statistisk analyse og omkostninger til disse, kan skabe et robust grundlag for prioriteringer.

Idet estimeringen af de totale antal produkter ikke har været en naturlig del af arbejdet med tilsyn og kontrol i dag, vil det være her, hvor den største forandring og indsats skal lægges i forhold til indsamling af information til modellen.

Det er vigtigt, at man fra starten får udformet en metode, som er konsistent for ikke at øge usikkerheden af estimaterne for det totale antal ulovlige produkter.

Ved gennemførelse af kontrol vil det være nødvendigt, at MST i forbindelse med planlægning af stikprøvekontroller fastlægger, med hvilken procent konfidenskontroller skal udmøntes. Det vil sige, med hvor stor sikkerhed er resultatet af kontrollen valid. For at operationalisere arbejdet med stikprøver kan det endvidere anbefales, at de udvalgte populationer stratificeres og opdeles i homogene grupper.

Der er en tæt sammenhæng mellem det statistiske konfidensniveau, stikprøvestørrelsen og udfaldsrummet af ulovlige produkter. Det er således ikke muligt isoleret at forudbestemme eller generelt fastlægge en ”fornuftig” stikprøvestørrelse, idet denne både afhænger af det valgte konfidensniveau og den ønskede ”præcision” af udfaldsrummet, dvs. hvor stort et interval, der accepteres.

Det er PwC’s umiddelbare vurdering, at der bør anvendes et konfidensniveau på mindst 80 %. Givet et konfidensniveau, et estimat for det samlede antal produkter på markedet og en stratifikation af populationen, vil der være givet en entydig fastlagt sammenhæng mellem stikprøvestørrelse og udfaldsrum.

Ved udtagelse af stikprøver er udfordringen at opnå et repræsentativt sample. På den baggrund bør eventuelle overvejelser i forbindelse med segmenteringen af markedet udnyttes i planlægningen af stikprøveudtagelsen. Selve modellen stiller ikke særlige krav derudover.

Der stilles heller ikke nogle særlige krav til stratifikation af populationen, men det bemærkes at udgangspunktet er, at jo flere strata, der anvendes, des flere stikprøver vil være nødvendige for at opnå samme præcision af udfaldsrummet. Det er PwC’s umiddelbare vurdering, at i de fleste tilfælde vil 2-3 strata være praktisk at arbejde med.

Det er PwC’s umiddelbare vurdering, at MST som udgangspunkt bør tilstræbe samme relative præcision i rapporteringen af kampagneresultater, fx ±20 %.

Ved formulering af eventuelle ”tommelfingerregler” til at fastlægge fornuftige stikprøvestørrelser bør alle ovenstående overvejelser tages i betragtning.

Den statistiske model er blevet implementeret i et Excel-regneark. Der er tale om en prototype, der primært skal illustrere de muligheder, som en it-løsning kan levere.

Det anbefales, at regnearket eller en tilsvarende løsning løbende udbygges og kvalitetssikres. I den forbindelse vurderes det, at følgende elementer kunne være relevante at modellere yderligere:

Sammenhæng mellem stikprøvestørrelser og omkostninger. Hvis modellen udvides med oplysninger om stikprøveomkostninger i de forskellige strata, så vil modellen kunne påbegynde at levere ”cost/benefit”-input til planlægningen af stikprøveudtagning.
Sammenhæng mellem stikprøvestørrelser og konfidens. Modellen vil forholdsvis let kunne udvides til at omfatte en funktion, der kan optimere stikprøvestørrelser i forhold til givne konfidensniveauer.
Sammenligning af kampagner. Det vil kunne være relevant at foretage opfølgning på tidligere udførte kampagner for eksempelvis at vurdere eventuelt ændret adfærd i de tilsynsbelagte virksomheder. I den forbindelse vil deciderede hypotesetest være et relevant værktøj.

Hjørnestenene i et framework er en segmentering af markedet, en struktureret dataindsamling og en dokumenteret statistisk model.

Implementeringen af ovenstående skal prioriteres. Det er rapportens umiddelbare vurdering, at følgende prioritering af opgaver er hensigtsmæssig:

Implementere den statistiske model
Påbegynde segmenteringsanalyser
Strukturere fremtidig dataindsamling
Analysere ”gamle” kampagner mv. med henblik på dataopsamling
Integrere økonomiske beslutningsvariable i modellen.

3 Indledning

3.1 Afgrænsning

Projektets overordnede formål har været at udvikle en stabil, robust og gennemskuelig metode til at opgøre effekten af Kemikalieinspektionens tilsyn og kontrol.

Med effekten af tilsynet menes de konklusioner vedrørende det totale antal af ulovlige produkter på markedet, som kan udledes på baggrund af de enkelte kampagner. Til dette formål er der udviklet en statistikmodel, der beskriver markedet ”as-is”, dvs. grundlæggende en statisk (”point in time” analyse).

Det kunne også være interessant for MST at undersøge de dynamiske virkninger af tilsynet, dvs. de ændringer i antallet af ulovlige produkter på markedet, der sker over tid. En forudsætning for en sådan dynamisk analyse er, at man kan beskrive ”før og efter”-tilstandene (i en statisk model). Umiddelbart vil det mest relevante statistiske værktøj til dynamiske analyser være hypotesetesten, der er simpelt beskrevet i appendiks (afsnit 12.4, ”Stikprøvestørrelser for hypotesetest”, side 44). Hvis der eksempelvis udføres analyser både før og efter en kampagne, så kan det testes, om man statistisk kan se en nedgang i antallet af ulovlige produkter. Modellering af dynamiske effekter af tilsyn og kontrol er ikke yderligere behandlet i denne rapport.

Fokus for effektvurderingen er de fire områder: Kosmetik, elektronik, legetøj samt klassificering og mærkning af kemiske stoffer og produkter. Der vil dog blive taget udgangspunkt i én fælles model for alle områder.

Ved vurdering af produktets lovlighed skelnes der i modellen mellem lovlig og ikke-lovlig (0 eller 1 variabel), hvorimod der ved en almindelig vurdering indgår subjektive forhold omkring lovligheden. Specielt ved mærkning af kemiske stoffer findes der bagatelgrænser for, hvornår et produkt erklæres ulovligt.

Der vil blive givet forslag til datakilder i forbindelse med information til brug for den statistiske model. Dette er dog ikke hovedformålet, og det må forventes, at der afsættes ressourcer til identifikation af relevante datakilder ved implementering af modellen.

Endvidere skal dybden af projektets resultater ses under iagttagelse af de tilstedeværende allokerede ressourcer/midler til projektets gennemførelse.

3.2 Vurdering af nuværende tilgang

MST administrerer kemikalieloven, som indeholder bestemmelser om klassificering, mærkning, indhold, anvendelse, godkendelse, salg og opbevaring af kemiske stoffer og produkter. En særlig enhed i MST - Kemikalieinspektionen - udfører tilsynet og kontrollen med, at importører, producenter og forhandlere af kemiske stoffer og produkter overholder reglerne.

Kemikalieinspektionen fører tilsyn med overholdelsen af reglerne i kemikalielovgivningen og de regler, der er knyttet til denne lovgivning – i alt ca. 50 forskellige bekendtgørelser, forordninger og cirkulærer. Kemikalielovgivningen er fortrinsvis baseret på EU-direktiver og forordninger. Tilsynsområdet spænder vidt – fra kosmetik til bly og bekæmpelsesmidler.

Kemikalieinspektionen gennemfører kampagner, som er tidsbegrænsede tilsyn på afgrænsede områder. Områderne skifter fra år til år. Kampagnerne gennemføres på de områder, der prioriteres højest i det pågældende år. Kampagner kan fx omfatte regler i en bekendtgørelse, en produktgruppe, en branche eller et geografisk område.

Kemikalieinspektionens placering i MST:

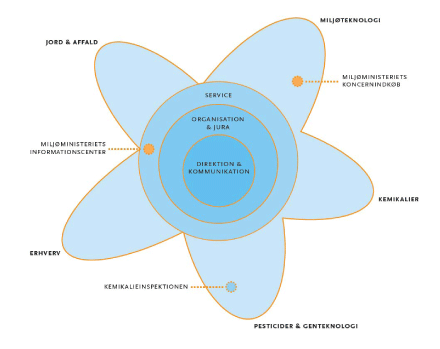
For at få indblik i MST’s nuværende tilgang til tilsyn og kontrol er denne gennemgået med henblik på videreudvikling af tilgangen og implementering af en statistisk metode. Gennemgangen er baseret på møder med nøglepersoner i MST^[1] samt materiale fra MST, herunder årsstatus, faktaark, projektbeskrivelser, kortlægninger mv.

Den nuværende tilgang indeholder mange gode elementer i form af kortlægninger, stikprøveudvælgelser og samarbejder med andre lande. Den er dog noget ustruktureret. Formålet med en ny metode er at bevare de allerede gode elementer, samtidig med at der kommer mere struktur over hele processen.

Selve udvælgelsen af stikprøverne bliver i dag gjort ad hoc og er baseret på information om nye regler, sundhedsmæssige konsekvenser, uopfordrede anmeldelser, information om ulovlige produkter fra kortlægninger osv. Det er efter vores opfattelse relevante elementer at inddrage i beslutningsprocessen, og der vil i den statiske model blive taget udgangspunkt i disse.

Foruden disse elementer foreslås det, at der inddrages andre elementer i beslutningsprocessen om, hvilke produkter der udtages til kontrol.

En mulig forbedring vil være at segmentere området, der kontrolleres, og se på, hvilke segmenter kampagnerne skal målrettes mod samt at få kvantificeret ”fokusværdien” for hvert segment. Ved at tillægge beslutningsvariable en foruddefineret værdi og tilsvarende vægt vil man med et tal kunne sammenligne fokus i de enkelte segmenter. På den måde vil man kunne få et bedre overblik over de kritiske segmenter og prioritere netop disse i forbindelse med stikprøver (dette er nærmere beskrevet i kapitel 5).

3.3 Dataanalyse

En model er en simplificering af virkeligheden. For at kunne inddrage de parametre, der bedst beskriver antallet af ulovlige produkter i en model, er det underliggende datagrundlag fra MST blevet analyseret.

Billedet omkring processerne går igen ved opsamling af data, og der findes ikke en struktureret metode for opsamling af data. Der findes dog megen information gemt i rapporter, årsberetninger og kortlægninger, som vil kunne bruges i en statistisk model.

Resultaterne af stikprøverne indeholder information om lovlighed, hvor stikprøven er taget, hvornår stikprøven er taget samt information omkring produktet.

Derudover findes information omkring tidsforbrug i allerede gennemførte budgetter. Dette er brugbart i forhold til at vurdere de ekstra omkostninger, den udvidede stikprøveanalyse vil koste.

Der har ikke været en naturlig proces for at vurdere antallet af ulovlige produkter ved estimeringen af det totale antal produkter. Der vil i nogle tilfælde af implementering af modellen være behov for indsamling af data, specielt omkring det totale antal produkter. En løsning kunne være at spørge direkte i butikken, hvor stikprøven bliver taget, omkring deres lager, antallet af solgte produkter osv. Desuden kan andre datakilder anvendes, fx Reach-IT, WEEE-System, produktregisteret, CVR-registeret og SKAT.

For fremtidig dataindsamling foreslås det, at der oprettes en database, hvor al relevant information samles på et sted i struktureret form.

[1] Se appendiks, afsnit 12.2, ”Kontaktpersoner i MST”, side 43.

4 Procesbeskrivelse af statistisk metode

Dette afsnit indeholder en beskrivelse af de processer, der skaber en statistisk metode.

Planlægning inden for statistik omhandler metoder, som gør målinger mere præcise. Hvis man bruger de korrekte metoder, kan måleusikkerheden for en stikprøve eller et eksperiment minimeres.

Formålet med denne statistiske metode er at kunne måle effekten af Kemikalieinspektionens tilsyn og kontrol inden for de fire tidligere nævnte områder. Dette kan opdeles i to dele; estimat for antallet af ulovlige produkter og usikkerheden omkring dette estimat.

Med effekt menes effekten af de enkelte tilsyn og kontroller i forhold til usikkerheden i resultaterne. Endvidere, hvor dækkende de gennemførte kampagner er - målt mod hele markedet.

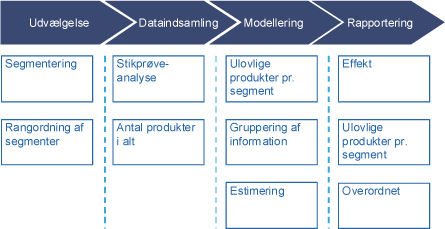
De enkelte processer i denne statiske metode kan opdeles i fire områder; udvælgelse, dataindsamling, modellering og rapportering.

Processen kan illustreres således:

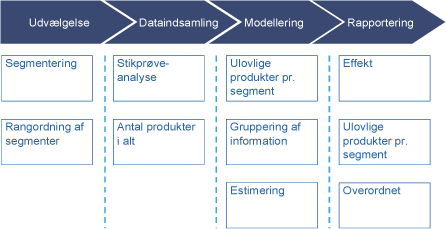
Udvælgelse

Udvælgelsesprocessen er en systematisk måde at finde de områder, som de næste kampagner skal rettes mod. Det første skridt er at segmentere markedet i logiske grupper set i forhold til modellen, praktik og eksisterende processer. Med praktik menes, at det skal være simpelt at kunne identificere den givne gruppe. Flydende definitioner som ”butikker der sælger bamser” er svære at definere. Legetøjsbutikker og elektronikbutikker i stormagasiner er en ”lettere” definerbar gruppe. Samtidig skal der tages højde for eksisterende tilgang, fx vil det være logisk at foretage segmenteringen baseret på de fire tilsynstyper. Der skal desuden tages højde for, at segmenteringen indeholder samme dimensioner som parametrene i modellen. Med det menes, at man skal være konsistent med de variable/parametre, man bruger i alle trin i processen for at estimere det samlede antal ulovlige produkter på markedet.

Når segmenteringen er på plads, vil der inden for hvert segment - ud fra foruddefinerede beslutningsvariable - blive vurderet på ”fokusværdien”. Fokusværdien er beregnet ud fra en værdi og vægt tildelt hver beslutningsvariabel. Værdien vil blive tildelt ved hjælp af nogle kriterier eller oversættelsestabeller og blive vægtet bestemt ud fra vigtigheden på den givne beslutningsvariabel sammenlignet med de resterende.

Dataindsamling

Dataindsamlingen dækker indsamlingen af information - både i form af stikprøveanalyse og det totale antal produkter. Stikprøveanalysen er en eksisterende proces hos Kemikalieinspektionen i dag, som kunne fortsætte i sin nuværende form. Desuden skal der opsættes processer for det totale antal produkter for at bestemme størrelsen af de gennemførte kampagner i forhold til helheden. Det vil være logisk at opdele både det totale antal produkter og stikprøver i samme segmenter som i udvælgelsesprocessen.

Modellering

Selve modelleringen indeholder mange aspekter, men generelt anvendes der som standard statistiske metoder tilpasset problemstillingen i MST. Resultatet af modellen er en forudsigelse af det totale antal ulovlige produkter samt usikkerheden af dette estimat. Modellen bygges på indsamlet information og opererer i de samme opdelinger, som findes i datagrundlaget.

Rapportering

Det, man skal være opmærksom på i rapporteringen, er, at der vil være forskellige måder at rapportere på, afhængigt af hvilken af de fire produkttyper der konkluderes på samt målgruppen for rapporteringen. Den statistiske formulering på baggrund af resultatet fra modellen vil dog altid være den samme, og der vil i rapporten blive givet forslag til direkte formuleringer, der kan anvendes.

5 Målretning af tilsyn og kontrol

For at kunne målrette Kemikalieinspektionens tilsyn og kontrol foreslås en segmentering af markedet for hver af tilsynstyperne. De enkelte segmenter vurderes derefter ud fra nogle foruddefinerede kriterier, hvor alle kriterier vægtes for at få den samlede score eller fokusværdi. Målretningen af kampagnerne vurderes så på baggrund af de enkelte scores i segmenterne.

5.1 Segmentering

De enkelte tilsynstyper foreslås segmenteret med relevante grupper i forhold til tilsyn og kontrol. Processen vedrørende estimeringen af det totale antal produkter vil på sigt blive lettere, idet arbejdet bliver struktureret. Det vurderes derudover, at der vil være behov for forskellige processer til de enkelte segmenter. Samtidig vil det mindske usikkerheden i estimaterne for antallet af ulovlige produkter, da segmenteringen vil gøre det muligt at gruppere på baggrund af, hvor meget information der findes på de enkelte områder.

Mulige segmenteringsvariable kunne være:

Tilsynstype
Produkt
Virksomhed (NACE-koder) eller andre inddelinger, fx størrelse
Opdeling i forhold til produkt-flow, kan der indhentes information tidligere i processen i form af toldpapirer eller lignende?
Geografi
Karakteristika på virksomheder, eventuelt størrelse, eller om virksomheden er en del af en kæde.

For at indhente information til segmenteringen kan der udsendes spørgeskemaer til virksomhederne vedrørende deres håndtering af produkterne i forhold til lovgivningen. Man skal dog være opmærksom på de specielle lovkrav, der eksisterer omkring indhentning af information. Det skal endvidere forsøges at stille neutrale spørgsmål, så selvinkriminering undgås. Fx vil spørgsmålet: ”Sælger I ulovlige produkter i henhold til Kemikalieinspektionens kontrol?” være et spørgsmål, der ikke er neutralt.

I medfør af kemikalielovens § 39 (jf. lovbemærkningerne fra 1978) kan MST indhente oplysninger til brug for den kortlægning og planlægning, som forudsættes at skulle iværksættes forud for en nærmere regulering. På den baggrund kan MST bede om visse data til brug for selve kampagnen. Dog skal det være information, der er ”need to know”, herunder hvorledes stikprøvestrategien udføres.

Ud fra svarene scores/rangordnes de enkelte virksomheder i forhold til sandsynligheden for, at de har ulovlige produkter. På den måde kan kritiske segmenter identificeres, allerede inden kampagnerne påbegyndes.

5.2 Udvælgelseskriterier

For at kunne vurdere de enkelte segmenter skal der opstilles et antal kriterier til vurdering af fokus. Samtidig skal kriterierne tildeles en foruddefineret vægt, for at kunne finde en samlet score i det givne segment. Scoren i hvert segment beregnes som følger:

, hvor

w_i = vægten for kriterium i, disse skal for alle n summe til 1

k_i = værdien for kriterium i

For at finde værdien af kriterierne, k kan de fx alle vurderes på en skala fra 1 til 4. Der behøver ikke være så mange grader at specificere kriteriet, k på. Skalaen bør indeholde et lige antal grader for at undgå for mange neutrale valg. Skalaen af scoren vil følge vurderingsskalaen, forudsat at vægtene, w summer til en.

Der findes mange kandidater til udvælgelseskriterierne, k, og de kan være forskellige samt have forskellige vægte, w tilsynstyperne imellem. Her er nogle eksempler på kriterier, k:

Politisk fokus
Mediefokus
Nye regler/regelændringer
Information fra kortlægninger
Indberetninger fra brancheforeninger
Indberetninger fra sundhedsvæsen
Sundhedsskadelige konsekvenser
Miljøskadelige konsekvenser
Effekt (beskrevet i modelkapitel)
Information fra andre lande
Antallet af uopfordrede anmeldelser fra privatpersoner eller lignende
Område, som historisk set har haft mange ulovlige produkter.

5.3 Implementering

En metode til at målrette tilsyn og kontrol skal bidrage med overblik over markedet, og det foreslås derfor, at der ikke anvendes mere end to variable i segmenteringen. Dermed vil segmenteringen altid kunne illustreres visuelt. En simpel model vil dog oftest være dårligere til at forklare virkeligheden, men stadig utrolig brugbar på grund af overblikket den giver.

Det er vigtigt, at man fra starten gør klart, hvordan man vil bruge modellen for at bedømme antallet af variable, men også specifikationen af dem, altså hvor mange grupper hver enkelt variabel skal tildeles.

Nogle valg kan være åbenlyse og bør udelukkes af modellen, fx kan det antages, at der altid gennemføres kampagner på områder med nye regler, og det vil derfor være naturligt ikke at have en model indeholdende nye regler som beslutningsvariabel.

Forholdet mellem segmenteringsvariable og udvælgelseskriterier, k kan variere meget i forhold til, hvilken segmenteringsmetode der bruges. Med segmenteringsmetode menes detaljeringsgraden i segmenteringen. Der kan også, før segmentering påbegyndes, foretages en opsplitning af produkterne, hvor de enkelte tilsynstyper vil være et oplagt valg. Det kan illustreres således:

Der vil også kunne bruges yderligere opsplitninger før segmenteringen, eksempelvis kan der efter valg af tilsynstype, opsplittes yderligere en variabel, som er forskellig pr. type. Det kan illustreres således:

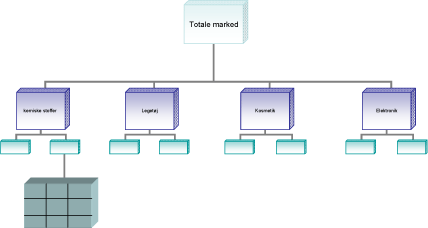
Her foretages en opsplitning - først på type og derefter på andre variable - hvorefter segmenteringen udføres.

En tredje mulighed kunne være at foretage segmenteringen af flere omgange, dvs. først foretages en segmentering på to variable, hvorefter der for hvert segmenteringsalternativ segmenteres på to variable. Det kan illustreres således:

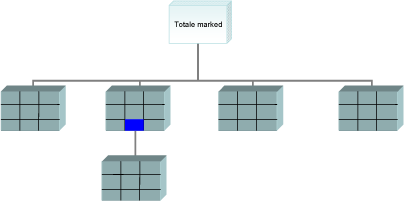
En sidste mulighed ville være at foretage segmenteringen indeholdende flere end to variable, hvor muligheden for grafisk fremstilling dog forsvinder. Det kan illustreres således:

Resultatet i alle metoder er den samme, men selve tankegangen omkring opsætningen vil være forskellig.

6 Stikprøvemetodik

Stikprøver bruges, når hele populationen ikke kan undersøges. Det kan være, at det er dyrt at foretage målingerne, eller at det ikke er fysisk muligt at undersøge mere end et udsnit af populationen. For eksempel er det ikke muligt at undersøge alt vandet i verdenshavene. Et andet problem, som statistik tager hensyn til, er, at målinger ofte er behæftet med usikkerhed, fejl eller mangler. Det kan for eksempel være målinger af den samme ting, hvor resultatet varierer for hver måling, men i gennemsnit har den korrekte (sande) værdi.

Stikprøvestørrelsen i en statistisk stikprøve er antallet af observationer. Det er typisk betegnet, n et positivt heltal (naturlige tal). Alt andet lige fører en større stikprøvestørrelse til øget præcision i forbindelse med vurdering af forskellige egenskaber af populationen. Dette kan ses i statistiske resultater som ”de store tals lov” og ”den centrale grænseværdisætning”. Gentagne målinger og replikation af uafhængige prøver er ofte påkrævet i forsøg på at nå den ønskede præcision.

Et typisk eksempel ville være, at man ønsker at bestemme gennemsnittet af en kontinuert stokastisk variabel (fx højden af en person). Hvis det antages, at der findes en stikprøve med uafhængige observationer, og variationen af populationen (målt ved standardafvigelsen σ er kendt, så er fejlleddet i stikprøven givet ved formlen:

Det ses, at hvis stikprøvens størrelse stiger, så går fejlleddet mod 0.

6.1 Estimering af andele med 95 % konfidens

Et typisk statistisk formål er at demonstrere, at den sande værdi af en parameter er inden for en afstand B af den estimerede værdi med 95 % sandsynlighed: B er fejlleddet, der mindsker med større stikprøvestørrelse, n. Værdien af B betegnes som 95 % konfidensinterval.

Det er ofte et ønske at estimere andele af den samlede population. I den sammenhæng vurderer vi grænserne for et 95 % konfidensinterval omkring den ukendte andel.

Ved et anvende et forsigtigt estimat, der er nærmere beskrevet i appendiks (afsnit 12.3, ”Udledning af fejlleddet”, side 43), kan vi opstille følgende simple sammenhæng (tommelfingerregel) mellem størrelsen på vores stikprøve og fejlleddet.

Man ser ofte disse tal citeret i nyhedsindslag med opinionsundersøgelser og andre stikprøveundersøgelser.

Givet et gennemsnit på 42 stikprøver pr. kampagne^[2], vil man med et 95 % konfidensniveau kunne sige, at estimatet baseret på stikprøven ikke afviger mere end ca. 15 % fra det sande gennemsnit.

Lad os udvide eksemplet til at ligne en kampagne. Vi har et segment, hvor vi ved, der er 10.000 forskellige produkter totalt. Der er i kampagnen testet 50 produkter, og der er fundet 15 ulovlige produkter.

Hvis man i stedet havde testet 100 produkter og fundet 30 ulovlige produkter, så andelen af ulovlige produkter stadig var 30 %, ville det forventede antal ulovlige produkter på hele markedet stadig være 1.000. Usikkerheden ville dog være blevet reduceret til 10 %.

Konklusionen vil så være, at med 95 % sandsynlighed vil det sande antal ulovlige produkter være mellem (30 %-10 %) * 10.000 = 2.000 og (30 %+10 %) * 10.000 = 4.000 enheder. Eller med 97,5 % sandsynlighed vil der være højst 4.000 ulovlige produkter.

Som nævnt er tommelfingerreglen, der er anvendt i de ovenstående beregninger, et estimat, der benytter den størst mulige usikkerhed (opnås for andelen 50 %) uafhængigt af den konkrete andel. På den baggrund kan man tale om et forsigtigt eller konservativt skøn.

6.2 Stratifikation

Ved stratifikation inddeles populationen i nogle (gensidigt udelukkende) dele - strata, og stikprøvestørrelser bestemmes for hvert stratum. Stratifikation kan være en fordelagtig metode, når der er stor forskel på variationen i de enkelte strata. Eller med andre ord, hvis variationen er mindre inden for de enkelte strata end variationen mellem strataene.

Et eksempel på stratifikation kunne være, at en vælgerundersøgelse deles op på beboere i parcelhuse, andelsboliger, lejligheder og andre boformer.

Der kan også gennemføres efterstratifikation ved hjælp af registrerede baggrundsvariable.

I forbindelse med tilsyn og kontrol ville det være en mulighed at segmentere kunderne efter forventet usikkerhed. Hvis der fx testes store kædebutikker, må der forventes ensartede resultater i de enkelte butikker (lav variation), hvorimod små specialbutikker er svære at definere som en homogen gruppe, og generelt må der forventes flere ulovlige produkter og mere variation i dette stratum.

Er specialbutikker en meget lille del af det samlede marked, kan der argumenteres for, at de udelades eller behandles homogent i modellen til estimering af de samlede antal ulovlige produkter på markedet.

[2] Gennemsnittet af de stikprøver, som indgår i tilsendt materiale omkring tidsforbrug

7 Estimat for det samlede antal produkter

For at kunne opskalere eller ekstrapolere resultaterne fra stikprøver skal der anvendes et estimat for det samlede antal produkter på markedet. Ved anvendelse af stratificerede stikprøver skal antallet af produkter i alle strata estimeres.

For bedste resultat skal dette gøres på samme segmentering som i udvælgelsesprocessen for tilsynsaktiviteterne. Har der i stikprøveanalysen været flere perspektiver, skal disse overvejes i forbindelse med estimatet.

Der findes i dag en god beskrivelse af, hvordan information kan indhentes i Kortlægningshåndbogen^[3], som inddrager mange interessante aspekter. Det foreslås at bruge samme metode som beskrevet der. I afsnit 5.1, ”Segmentering”, side 17 er givet forslag til variable.

Ved opgørelse af det totale antal produkter er det vigtigt at have en klar definition af, hvad der skal opgøres. Er det salget, lagerbeholdningen eller noget tredje? Rent intuitivt må det være det totale antal produkter, som bliver anvendt af forbrugere, da eksponeringen mod de farlige stoffer findes der. Det ville kunne opgøres ved at tage salget i den sidste periode. Længden af perioden afhænger af den forventede levetid for det enkelte produkt.

Med hensyn til usikkerheden omkring det totale antal produkter vil en mulighed være at henføre det direkte til datakilden. Har man en gang analyseret usikkerheden for en datakilde, vil usikkerheden kunne antages at være den samme fremover. Detaljerede analyser vil have lille usikkerhed. Tal fra Danmarks Statistik, Reach-IT, WEEE-System, produktregisteret, CVR-registeret og SKAT samt information fra brancheforeninger vil have lidt større usikkerhed, men stadig lille. Datakilder som De Gule Sider og Google vil have stor usikkerhed og bør undgås ved estimeringen af det totale antal produkter.

For at minimere indsatsen ved indsamling af informationen kan der eventuelt spørges direkte i butikken, hvor stikprøven bliver taget, omkring antallet af dette produkt. Det kunne fx være antallet af produkter på lager, hvor mange styk butikken har solgt af dette produkt, og hvad de forventer af salg og køb i fremtiden.

Denne rapport vil ikke anføre konkrete forslag til datakilder.

[3] Manual til kortlægning af producenter, importører og forhandlere, Miljøprojekt Nr. 1242 2008

8 Statistisk model

Formålet med formuleringen af en statistisk model er at kunne beskrive det samlede antal ulovlige produkter ud fra

et estimat for det samlede antal produkter på markedet
antallet af ulovlige produkter fundet ved stikprøve.

Vi vil først præsentere en generel tilgang til statistisk modellering. Derefter vil vi beskrive en simpel model med to sandsynlighedsfordelinger, som kan udvides til en stratificeret model.

8.1 Generelt

Udgangspunktet for den statistiske analyse er et sæt af observationer. Dette kunne fx være resultatet af en undersøgelse af et antal legetøjsprodukter for indhold af ftalater. Hvis observationen er givet ved {0, 0, 0, 1, 0, 0, 0, 1, 1, 0}, betyder det, at det fjerde, det ottende og det niende produkt havde udfaldet ”succes” (hér: indhold af ftalater, dvs. ulovligt produkt).

Vi vil i almindelighed bare tale om én observation, selv om det kan dreje sig om mange målinger. En observation er således en vektor x=(x₁,...,x_n) af tal. Observationen antages formelt at være en realisation af en stokastisk variabel X=(X₁,...,X_n). X’s værdier tilhører udfaldsrummet E, mængden af mulige udfald.

Idéen med at indføre den stokastiske variabel X er, at vi sammen med vores observation X betragter alle de andre udfald, vi kunne have fået. Ved hjælp af den statistiske model prøver vi så at beskrive usikkerheden omkring udfaldet ved en eller flere sandsynlighedsfordelinger. Ofte har man et vist kendskab til fordelingen for X. Måske ved man, at X’s fordeling er en binomialfordeling, men ved ikke hvad sandsynlighedsparameteren er. På grundlag af en eller flere observationer vil vi så prøve at skønne over, hvilken binomialfordeling der er den rigtige. Det, vi kalder den statistiske model, er mængden af de mulige sandsynlighedsfordelinger. For at holde rede på dem indicerer man dem. Dette sker så vidt muligt på en naturlig måde. En sådan mængde af sandsynligheder plejer man i statistikken at kalde en familie af sandsynligheder.

Formelt siger vi, at en statistisk model er en indiceret familie (Ρ_θ)_θεΘ af sandsynlighedsfordelinger på E, således at for hvert θ er Ρ_θ en mulig fordeling af X. Indeksmængden Θ kaldes parameterområdet, og θ kaldes parameteren.

At vælge en fordeling på grundlag af observationen X kaldes at estimere. Man plejer her at identificere fordelingen Ρ_θ med dens parameter θ og taler så om at estimere parameteren θ. Hvis man ved 100 kast med en skummel og skævt udseende mønt har fået krone 33 gange og bliver bedt om at give et skøn over, hvad sandsynligheden for krone ρ er, vil det være nærliggende at vælge ρ=0,33, hvis man i øvrigt ikke ved noget om mønten. Estimation betyder altså, at vi ud fra observationen x prøver at bestemme den fordeling, som vi tror x kommer fra. Ser vi igen på binomialfordelingen, er der selvfølgelig ingen grund til at tro, at ρ netop er 0,33, men nok at ρ ligger nær 0,33. Havde udsagnet været baseret på 330 kroner ud af 1.000 kast, ville man nok have været mere overbevist om, at 0,33 kunne være det rigtige.

Der findes mange forskellige estimeringsmetoder, dvs. forskrifter, der fortæller, hvordan man i en given model vælger en fordeling på grundlag af et sæt af observationer. En sådan forskrift, der altså er en funktion af observationerne, kaldes en estimator. Vi vil holde os til den såkaldte maksimaliseringsmetode. Denne metode giver i almindelighed fornuftige estimatorer.

Det engelske ord for maksimaliseringsestimator er maximum likelihood estimator. Derfor bruges forkortelsen ML-estimator ofte for maksimaliseringsestimatoren.

Hvis X er binomialfordelt, dvs. , da er maksimaliseringsestimatoren for sandsynligheden ρ entydigt bestemt og givet ved

8.2 Simpel model

Vi vil tage udgangspunkt i en model uden stratifikation. Vi betragter således populationen af produkter som en helhed uden underopdeling.

Til at beskrive antallet af ulovlige produkter i populationen vil vi anvende to sandsynlighedsfordelinger: binomialfordelingen og normalfordelingen. Vi antager, at antallet af ulovlige produkter er binomialfordelt med antalsparameter og sandsynlighedsparameter ρ , og vi antager, at antalsparameteren er normalfordelt med middelværdi µ og varians σ². Idet antalsparameteren i binomialfordelingen skal være et naturligt tal, vil vi i praksis anvende afrundede værdier af normalfordelingen. Den statistiske betydning af at anvende afrundede værdier er i denne sammenhæng bagatelagtig.

Formelt har vi:

I forbindelse med stikprøveudtagning betegnes antallet af observationer i stikprøven π og antallet af ”succeser” (ulovlige produkter) υ.

Notationen kan illustreres i nedenstående figur:

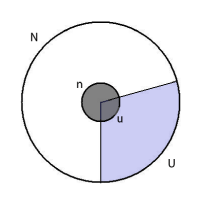
Den yderste cirkel repræsenterer hele markedet, og den inderste mørke cirkel repræsenterer den udtagne stikprøve. Idet andelen af ulovlige produkter i stikprøven (u/n) antages at svare til andelen af ulovlige produkter på hele markedet (U/N), kan U bestemmes ud fra N, n og u.

I appendiks er de væsentligste statistiske egenskaber for udledt, og det fremgår, at middelværdi og varians af den stokastiske variabel er givet ved:

Eksempel I (simpel model):

Vi forventer, at det samlede antal produkter på markedet er 10.000 med standardafvigelse på 15 % (dvs. med 95 procents konfidens forventes det, at antallet af produkter tilhører intervallet [7000,13000], svarende til 10000 ± 2 · 1500). Vi udtager en stikprøve på 50 produkter. Lad stikprøvens resultat være 15 ulovlige produkter. Vi har således n=50 og u=15. ML-estimatet for sandsynlighedsparameteren i binomialfordelingen baseret på vores observation (stikprøve) vil være , og på den baggrund vil vi skønne, at der er 10000 · 0,3=3000 ulovlige produkter på markedet. Men usikkerheden af vores skøn vil afhænge, dels af variansen på vores estimat af det samlede antal produkter på markedet (givet ved σ² =1500²), og dels af variansen af vores estimat for ”succes”-sandsynligheden (givet ved ρ²=ρ(1-ρ)/n=0,0042). Den samlede usikkerhed af vores skøn er givet ved standardafvigelsen for , der i dette eksempel udgør svarende til 26,5 %. Konklusionen er således, at det forventede antal ulovlige produkter på markedet med 95 procents konfidens tilhører intervallet [1410,4590], svarende til 3000 ± 2 · 795.

8.3 Model med stratifikation

Formålet med at indføre stratifikation i modellen er at reducere usikkerheden (målt ved standardafvigelsen) på estimatet af antallet af ulovlige produkter. Stratifikation er således et middel til at optimere udnyttelsen af ressourcer i forbindelse med stikprøveudtagning.

Den simple model, der blev beskrevet i forrige afsnit, udvides nu til også at omfatte stratifikation, dvs. at populationen af produkter underopdeles i lag (strata).

Vi vil stadig anvende binomialfordelingen og normalfordelingen til at beskrive antallet af ulovlige produkter i populationen, men nu antager vi, at populationen er inddelt i k uafhængige strata. Vi antager, at antallet af ulovlige produkter i det i’te strata er binomialfordelt med antalsparameter og sandsynlighedsparameter ρ_i, og vi antager, at antalsparameteren er normalfordelt med middelværdi µ_i og varians σ_i².

I forhold til Kemikalieinspektionens nuværende tilgang er det ”nye”, at der skal estimeres (antages) en varians/standardafvigelse af populationernes størrelse i de enkelte strata.

Formelt har vi:

Og antallet af ulovlige produkter i hele populationen fås ved at summere over alle strata:

8.4 Stikprøvestørrelse i model med stratifikation

Til at bestemme de optimale stikprøvestørrelser i en stratificeret model anvender vi Neymans allokeringsmetode^[4]. Metoden giver en optimal stikprøveallokering baseret på middelværdier og standardafvigelser i de enkelte strata.

Lad n_i^* betegne den optimale stikprøvestørrelse fra det i’te strata:

Antallet af stikprøver fra de enkelte strata kan illustreres i nedenstående figur:

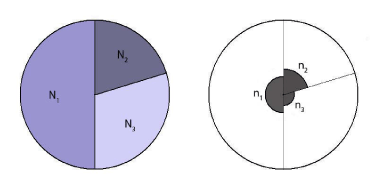
Cirklen i venstre side repræsenterer beskrivelsen af hele populationen, hvor farven, hørende til de enkelte strata, er en illustration af variansen (jo større varians desto mørkere farve). Cirklen i højre side repræsenterer stikprøven baseret på Neymans allokeringsmetode. Det ses af figuren, at metoden medfører, at der udtages relativt flest stikprøver fra strata med størst varians.

Hvis antallet af stikprøver fra den samlede population er givet, så er den optimale allokering af stikprøvestørrelser fra de enkelte strata entydigt givet ud fra middelværdier og standardafvigelser i de k forskellige normalfordelinger, der beskriver det samlede antal produkter i hvert stratum.

8.5 Analyse af stikprøve

På baggrund af resultatet af stikprøverne kan den ”mest sandsynlige” frekvens af ulovlige produkter bestemmes for hvert stratum, hér anvendes ML-estimatoren, der i sig selv er en stokastisk variabel med en standardafvigelse, der afhænger af u og n.

Næste skridt er at kombinere stikprøveanalysen med estimatet for det samlede antal produkter.

Formelt haves nu for alle strata:

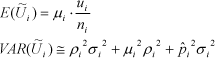
Formel

Alle resultater i modellen bygger på den antagelse, at de normalfordelinger, der beskriver den samlede population i de enkelte strata, er uafhængige. Der kan argumenteres for, at der vil være tendens til, at man enten konsekvent over- eller undervurderer middelværdi og varians i de forskellige strata, og at fordelingerne dermed ikke er uafhængige. Hvis uafhængighedsantagelsen ikke holder, vil den stratificerede model undervurdere usikkerheden, og det er på den baggrund afgørende for den statistiske models relevans at sikre, at de normalfordelinger, som beskriver de enkelte strata, er uafhængige.

8.6 Statistisk konklusion

Der er umiddelbart tre typer af konklusioner, som kan foretages på baggrund af den statistiske model.

På baggrund af estimatet for det samlede antal produkter på markedet og den udtagne stikprøve kan MST med {konfidensniveau} procents sikkerhed sige, at antallet af ulovlige produkter på markedet udgør mellem {min} og {max}.
På baggrund af estimatet for det samlede antal produkter på markedet og den udtagne stikprøve kan MST med {konfidensniveau} procents sikkerhed sige, at antallet af ulovlige produkter på markedet udgør mindst {min}.
På baggrund af estimatet for det samlede antal produkter på markedet og den udtagne stikprøve kan MST med {konfidensniveau} procents sikkerhed sige, at antallet af ulovlige produkter på markedet udgør højst {max}.

Konklusion 1 er tosidet, mens konklusion 2 og 3 er ensidede. Der gælder følgende sammenhæng:

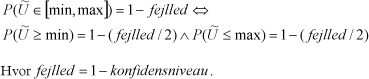
Formel

8.7 Samlet fremgangsmåde

Den samlede fremgangsmåde i forbindelse med planlægning, udtagning, analyse og konklusion af stikprøver kan opsummeres i følgende punkter:

Eksempel II (stratificeret model):
Lad igen estimatet for det samlede antal produkter på markedet være givet ved 10.000, men nu er markedet underopdelt i tre uafhængige strata. For hvert stratum skal der estimeres middelværdi og varians/standardafvigelse. Lad disse være givet ved følgende tabel:


Stratum, i	1	2	3
Middelværdi, µ_i	5.000	3.000	2.000
Standardafvigelse, σ_i	10 %	15 %	27,5 %

Bemærk, at det vægtede gennemsnit af de anvendte standardafvigelser er

15 %, dvs. lig med standardafvigelsen i eksempel I. Det skal dog vise sig, at standardafvigelsen af det samlede antal produkter på markedet i dette eksempel kun udgør 8,7 %! Der gælder nemlig, at standardafvigelsen omkring summen af uafhængige normalfordelte variable er mindre end summen af standardafvigelserne på de enkelte variable.

Vi udtager igen i alt 50 produkter, men denne gang underopdeles stikprøven i tre del-stikprøver. For at minimere den forventede varians af det samlede estimat anvendes Neymans allokeringsmetode, der medfører, at der skal udtages stikprøver fra det første stratum. Tilsvarende beregninger gennemføres for det andet og tredje stratum.

Lad resultatet af stikprøverne være givet ved følgende tabel:


Stratum, i	1	2	3
Stikprøve, n_i	25	14	11
Ulovlige, µ_i	8	4	3

Vi kan nu beregne ML-estimaterne for ’erne, der sammenholdt med

µ_i’erne giver os de forventede værdier af det samlede antal ulovlige produkter i hvert stratum. For det første stratum forventes således ulovlige produkter. Vi kan også beregne -estimatorernes standardafvigelser ρ_i. For det første stratum fås således:

Ved at sammenholde standardafvigelserne på ’erne med standardafvigelserne på ’erne kan vi beregne standardafvigelserne på estimatet af det samlede antal ulovlige produkter i det i’te stratum. Lad τ_i betegne standardafvigelsen på . Vi har således:


Stratum, i	1	2	3
Middelværdi,	1.584	880	540
Standardafvigelse, τ_i	491	397	314
Varians	491²	397²	314²

Næste skridt i analysen er at konsolidere resultaterne fra de enkelte strata til den samlede population. Vi udnytter, at variansen af uafhængige normalfordelinger er ”additiv”, dvs. at summen af varianserne er lig med variansen af summen. Vi får således, at variansen af , dvs. det samlede antal ulovlige produkter i hele populationen er lig med 491² + 397² + 314²= 491624, og standardafvigelsen af det samlede antal ulovlige produkter i hele populationen er dermed givet ved:

Det kan ses, at denne standardafvigelse er 12 % mindre end den tilsvarende standardafvigelse i eksempel I. Reduktionen skyldes, at en del af variationen, der er inden for de enkelte strata, ”udjævnes”, når man betragter hele populationen.

Med middelværdi og standardafvigelse på plads kan vi foretage statistiske konklusioner på baggrund af forskellige konfidensniveauer. I tabellen nedenfor er konfidensintervallerne angivet for en række ofte anvendte konfidensniveauer.


	Konfidensinterval
Konfidensniveau	Nedre grænse	Forventet værdi	Øvre grænse
80 %	2.414	3.004	3.594
90 %	2.105	3.004	3.903
95 %	1.851	3.004	4.157
97,5 %	1.630	3.004	4.378

Ved anvendelse af 95 procents konfidens ses det, at konfidensintervallet udgør [1851,4157], dvs. at på baggrund af estimatet for det samlede antal produkter på markedet og den udtagne stikprøve kan vi med 95 procents sikkerhed sige, at antallet af ulovlige produkter på markedet udgør mellem 1851 og 4157.

8.8 Excel-værktøj

Den statistiske model er blevet implementeret i et Excel-regneark. Der er tale om en prototype, der primært skal illustrere de muligheder, som en it-løsning kan levere.

I første omgang leverer regnearket den optimale allokering af del-stikprøver på baggrund af en række input om den samlede population og stikprøvestørrelse. På baggrund af faktiske stikprøveresultater leverer regnearket middelværdi og standardafvigelse af den stokastiske variabel, der beskriver det samlede antal ulovlige produkter. I et særskilt faneblad ”oversættes” resultaterne vedrørende middelværdi og standardafvigelse til konfidensintervaller ved anvendelse af forskellige konfidensniveauer.

Herunder er indsat eksempler på skærmbilleder fra Excel-modellens to nuværende faneblade:

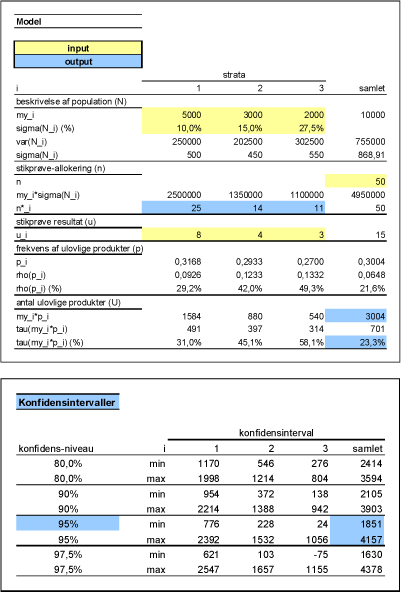
Det anbefales, at regnearket eller en tilsvarende løsning løbende udbygges og kvalitetssikres. I den forbindelse vurderes det, at følgende elementer kunne være relevante at modellere yderligere:

Sammenhæng mellem stikprøvestørrelser og omkostninger. Hvis modellen udvides med oplysninger om stikprøveomkostninger i de forskellige strata, så vil modellen kunne påbegynde at levere ”cost/benefit”-input til planlægningen af stikprøveudtagning.
Sammenhæng mellem stikprøvestørrelser og konfidens. Modellen vil forholdsvis let kunne udvides til at omfatte en funktion, der kan optimere stikprøvestørrelser i forhold til givne konfidensniveauer.
Sammenligning af kampagner. Det vil kunne være relevant at foretage opfølgning på tidligere udførte kampagner for eksempelvis at vurdere eventuelt ændret adfærd i de tilsynsbelagte virksomheder. I den forbindelse vil deciderede hypotesetest være et relevant værktøj.

En fuldt udbygget model vil således samlet kunne vurdere stikprøvestørrelser (fordelt på strata), konfidens af resultater og omkostninger forbundet med udtagelsen. Disse input kan i sammenhæng med den overordnede segmentering (beskrevet i afsnit 5, ”Målretning af tilsyn og kontrol”, side 17) give værdifuldt input til udvælgelse og prioritering af Kemikalieinspektionens fremtidige kampagner.

[4] J. Neyman: ”On two different aspects of the representative method: the method of stratified sampling and the method of purposive selection,” J. R. Statist. Soc. 97 (1934), 558-606.

9 Omkostninger ved implementering af nyt framework

Med framework menes den samlede struktur relateret til planlægning, udvælgelse, udtagelse, analyse og rapportering af stikprøver. Hjørnestenene i et framework er en segmentering af markedet, en struktureret dataindsamling og en dokumenteret statistisk model.

Med omkostninger forstås i første omgang de ressourcer, som MST skal sætte af for at implementere det i rapporten beskrevne framework i henhold til det nuværende ambitionsniveau.

Idet implementeringen af den statistiske model vil synliggøre usikkerheden i de statistiske konklusioner, som stikprøverne giver anledning til, kan implementeringen i sig selv give anledning til øgede omkostninger, hvis ambitionsniveauet i forhold til det nødvendige antal af stikprøver øges. Hvis MST fx beslutter, at der højst kan accepteres et givet spænd mellem (i) det forventede antal ulovlige produkter på markedet og (ii) det antal af ulovlige produkter, som man med et givet konfidensniveau kan sige, at antallet ikke vil overstige, så kan dette medføre et øget ambitionsniveau, dvs. at der skal udtages flere stikprøver i de enkelte kampagner.

Det antages i vurderingen af omkostningerne, at information om totalt antal ulovlige produkter opbygges, efterhånden som nye kampagner bliver gennemført. Det totale antal ulovlige produkter i segmenter, som tidligere er blevet testet, vil derfor ikke blive estimeret.

Følgende tiltag er vurderet:

Indsamling af information (stikprøver og totale antal produkter)
Segmentering af markedet (herunder udvælgelseskriterier)
Opbygning af model (forståelse og opbygning af model i Excel).

Det er svært at definere, hvad der kommer først i forhold til dataindsamling og segmentering, da man skal have en segmentering, inden man kan starte på dataindsamlingen, men segmenteringen vil afhænge af, hvad der er muligt i dataindsamlingen. Så der vil være en iterativ proces mellem segmenteringen og dataindsamlingen.

Dataindsamling

Der findes i dag information fra allerede gennemførte kampagner, som dog skal struktureres. Der findes mange muligheder for indhentning af information, som allerede er brugt hos MST i dag. Der kan eventuelt suppleres med nye datakilder enten i form af andre dataudbydere, spørgeskemaundersøgelser, faciliteret af MST, eller direkte spørgsmål til virksomhederne under kampagnerne. Specielt for det samlede antal produkter skal der lægges ressourcer, da der ikke findes en indsamlingsproces i dag.

At vurdere omkostninger i forhold til dataindsamlingen afhænger meget af de beslutninger, der tages i forbindelse med opbygning af database og datakilder, men et minimumsestimat for udviklingen af en struktureret opsamling af data er ca. 150 timer. Estimatet er baseret på en Excel-baseret database uden brug af spørgeskemaundersøgelser.

Opsætning af segmentering af markedet

Segmentering og udvælgelse kræver, at man - for at få en stabil metode - beslutter sig for de enkelte segmenteringsvariable og udvælgelseskriterier, inden estimeringen påbegyndes. Dvs. der skal udføres en del analysearbejde i forhold til segmenteringen for at fastlægge beslutningsvariablene.

Som udgangspunkt vil der skulle foretages en markedssegmentering pr. kontrolområde.

Som tidligere anført hænger beregnet ressourceforbrug meget sammen med dataindsamlingen. Der vil som minimum skulle forventes omkring 200 timers arbejde til opsætning af segmenteringen. Der skal opbygges helt nye processer - her i form af nye datakilder, segmenteringsmetode, vurdering af bedste segmenteringsvariable og udvælgelseskriterier. Samtidig skal der vurderes på vægtene for de enkelte udvælgelseskriterier.

Ibrugtagelse af Excel-værktøj

Da værktøjet vil blive brugt ad hoc, efterhånden som kampagnerne bliver gennemført, vurderes det ikke umiddelbart nødvendigt at indarbejde det i et decideret produktionsmiljø. På den baggrund er ressourceforbruget til ibrugtagelse af modellen estimeret til ca. 75 timer. Estimatet tager udgangspunkt i en implementering af prototypen, der er beskrevet i afsnit 8.8, ”Excel-værktøj”, side 34.

Udvidelse af model og værktøj

Tidsestimatet for udbygning af den statistiske model, herunder eventuelle it-værktøjer, vil være afhængig af, hvordan segmenteringen ser ud, og hvor detaljeret en stratificering der ønskes. Derudover er det også væsentligt for estimatet, om modellen primært skal anvendes til statiske analyser, eller om den også skal kunne anvendes til dynamiske analyser, fx hypotesetest.

I henhold til de anbefalede udvidelsesmuligheder beskrevet i afsnit 8.8 ” Excel-værktøj”, side 34, forventes et tidsforbrug på ca. 100 timer.

10 Konklusion og anbefalinger

På baggrund af en gennemgang af MST’s Kemikalieinspektions nuværende metodik for effektvurdering giver denne rapport et oplæg til samlet framework for stikprøvemetodik, dataindsamling og effektberegning.

Projektet har fokuseret på udviklingen af en robust, dokumenteret statistisk model samt en metode til målretning af det fremtidige tilsyn baseret på segmentering.

I afsnit 5, ”Målretning af tilsyn og kontrol” præsenterer rapporten et oplæg til den fremtidige strukturering af stikprøveudtagelse og øvrig dataindsamling.

I afsnit 8, ”Statistisk model” udleder og dokumenterer rapporten en model, der kan analysere og konkludere på MST’s nuværende praksis og samtidig fungere som base for mere avancerede statistiske analyser, som fx dynamiske analyser.

På baggrund af ovenstående analyser er det rapportens anbefaling, at der påbegyndes en gradvis implementering. Tiltagene vurderes at kunne medføre flere fordele:

På kort sigt kan implementeringen af den statistiske model underbygge og dokumentere den nuværende tilgang til udtagning og analyse af stikprøver.
På lidt længere sigt kan udviklingen af en metode, hvor der er sammenhæng mellem omkostninger og diverse beslutningsvariable, fx hvilke områder skal udvælges til kampagner? Hvor mange stikprøver skal udtages i hver kampagne? Hvilket statistisk konfidensniveau skal anvendes? Hvor mange kampagner kan/skal gennemføres årligt?

Det er rapportens vurdering, at en model, der både inddrager dataindsamling, stikprøveudtagelse, statistisk analyse og omkostninger til disse, kan skabe et robust grundlag for prioriteringer.

Implementeringen af ovenstående skal prioriteres. Det er rapportens umiddelbare vurdering, at følgende prioritering af opgaver er hensigtsmæssig:

Implementere den statistiske model
Påbegynde segmenteringsanalyser
Strukturere fremtidig dataindsamling
Analysere ”gamle” kampagner mv. med henblik på dataopsamling
Integrere økonomiske beslutningsvariable i modellen.

I tilknytning til ovenstående anbefales det, at den statistiske model og dertil knyttede it-værktøjer løbende tilpasses.

11 Definitioner

Binominalfordeling:

En diskret fordeling inden for sandsynlighedsregning. Den er en af de mest fundamentale og samtidig meget grundlæggende fordelinger. Meget kort fortalt beskriver den sandsynligheden for at få k-succeser i n-forsøg.

Ekstrapolere:

Bestemme en tilnærmet værdi for variable på baggrund af allerede givne værdier.

Framework:

Den samlede struktur relateret til planlægning, udvælgelse, udtagelse, analyse og rapportering af stikprøver.

Hypotesetest:

En statistisk metode, der benyttes til at undersøge, om en hypotese understøttes af en stikprøve eller ej.

Indiceret familie:

En mængde af sandsynlighedsfordelinger sorteret efter indekstegn.

Konfidens:

Den grad af sikkerhed, hvormed statistiske konklusioner kan udtales.

Kontinuert stokastisk variabel:

I statistik bruges kontinuert om en nummerisk stokastisk variabel (se beskrivelse nedenfor), som kan antage reelle eller komplekse værdier (eventuelt inden for et interval) i modsætning til en diskret variabel, som kun kan antage heltalsværdier (eller en endelig mængde reelle eller komplekse værdier).

Kortlægningshåndbogen:

Manual, der beskriver en metode til at identificere aktører beskæftiget med udvalgte produktgrupper.

Miljøstyrelsen:

Forkortes MST

NACE-koder:

Opdeling af virksomhedsbrancher i sekscifrede koder.

PricewaterhouseCoopers:

Forkortes PwC

Segmenteringsvariable:

Faktorer, der danner baggrund for opdeling af markederne under tilsyn.

Statisk model:

Model, der ikke inddrager udviklinger over tid (modsat dynamisk).

Stokastisk variabel:

En type variabel, der beskriver et tilfældigt forsøg, hvor udfaldet ikke er kendt.

Stratifikation:

Opdeling af den samlede population i homogene grupper (strata-lag).

Symboler:

De græske tegn, der er anvendt i den statistiske model, er:

Tegn	Udtale
µ	My
σ	Sigma
ρ	Rho
τ	Tau

12 Appendiks

12.1 Materiale modtaget fra MST

Smykkekortlægning:

http://www2.mst.dk/common/Udgivramme/Frame.asp?
http://www2.mst.dk/Udgiv/publikationer/2008/978-87-7052-773-6/html/default.htm

Negleprojekt:

http://www.mst.dk/Udgivelser/Publikationer/2008/07/978-87-7052-786-6.htm

Projektbeskrivelse for et tilsynsprojekt:

Modtaget i Word

Designguide, logo og retningslinjer for opbygningen af udgivelser og projektartikler fra MST:

http://www.mst.dk/Kontakt/Specielt+for+leverandører/Designprogam/

Årsberetninger:

http://www.mst.dk/Kemikalier/Kontrol+og+tilsyn/Aarsberetninger/

Tidsforbrug pr. produkt:

Modtaget i Word

Manual til kortlægning af producenter, importører og forhandlere:

http://www2.mst.dk/common/Udgivramme/Frame.asp?http://www2.mst.dk/ udgiv/publikationer/2008/978-87-7052-800-9/html/default.htm

RoHS substances (Hg, Pb, Cr(VI), Cd, PBB and PBDE) in electrical and electronic equipment in Belgium:

Modtaget i pdf

12.2 Kontaktpersoner i MST

PwC har haft kontakt med følgende personer i MST:

Flemming Hovgaard Jørgensen
Birte Børglum
Dorrit Skals.

12.3 Udledning af fejlleddet

En tommelfingerregel for (maksimal eller ”konservativ”) andelen B kan udledes af, at estimatet for en andel, (hvor X er antallet af ”succes”-observationer) er en binomial fordeling, som har en maksimal varians på 0,25 for parameter ρ = 0,5). Så stikprøven X/n har højst en varians på 0,25/n. For tilstrækkeligt store n vil fordelingen kunne estimeres ved en normalfordeling med det samme gennemsnit og varians.

Denne tilnærmelse kan bruges til at påvise, at 95 % af denne fordelings sandsynlighed ligger inden for to standardafvigelser af gennemsnittet. Derfor vil et interval af formen:

danne et 95 procents konfidensinterval omkring den sande andel.

Hvis vi kræver, at fejlleddet ε ikke overstiger grænsen B, kan vi løse ligningen:

som giver os

12.4 Stikprøvestørrelser for hypotesetest

Et almindeligt problem for statistikere er beregning af stikprøvestørrelsen krævet til at give en vis præcision til en stikprøve, givet en forudbestemt Type I-error α (fejlmargin). Et typisk eksempel for dette følger:

Lad x_i, i = 1, 2, ..., n være uafhængige observationer fra en normalfordeling med middelværdi µ og varians σ². Lad os betragte to hypoteser, en nul-hypotese:

H₀: µ = 0

og en alternativ hypotese:

H_alt: µ = µ^*

for en ”mindste signifikante forskel” µ^* > 0. Dette er den mindste værdi, som vi interesserer os for i forbindelse med at iagttage en forskel.

Hvis vi ønsker at (1) forkaste H₀ med en sandsynlighed på mindst 1-β, når H_alt er korrekt (dvs. en styrke på 1- β), og (2) afvise H₀ med sandsynlighed α, når H_alt er sand, så får vi brug for følgende:

Hvis z_α er den øvre α -procentpoint-værdi af standard-normalfordelingen (middelværdi 0 og varians 1), så gælder det at:

og udsagnet ”forkast H₀, hvis vores stikprøvegennemsnit α er større end ”, er en beslutningsregel, der opfylder (2). (Bemærk, at der her er tale om en ensidet test).

Nu ønsker vi, at dette kan ske med en sandsynlighed på mindst 1- β, når H_alt er sand. I dette tilfælde vil vores stikprøvegennemsnit komme fra en normalfordeling med middelværdi µ^*. På den baggrund vil vi kræve, at:

Ved omskrivning kan det vises at være opfyldt, når

hvor Φ er normalfordelingens fordelingsfunktion.

12.5 Udledning af den statistiske model

I det følgende beskrives udledningen af den statistiske model til beskrivelse af det samlede antal ulovlige produkter på markedet.

I tabellen nedenfor er de væsentligste statistiske egenskaber ved normalfordelingen og binomialfordelingen anført:


Fordeling	Middelværdi	Varians	Standardafvigelse
Bin(n,ρ)	n · ρ	nρ(1-ρ)
N (µ, σ²)	µ	σ²	σ

Antal produkter i populationen, N

Det samlede antal produkter i populationen, , antages at være normalfordelt med parametre µ og σ, dvs. formelt:

De statistiske egenskaber ved fordelingen for er ligetil:

Frekvensen af ulovlige produkter i populationen, ρ

Frekvensen af ulovlige produkter i populationen, ρ, estimeres på baggrund af en stikprøve givet ved:

Antallet af observationer, n og antallet af fundne ulovlige produkter, u.

ML-estimatet for ρ er dermed givet ved (idet vi ser usom realisationen af en binomialfordelt stokastisk variabel):

ML-estimatoren også er binomialfordelt, man siger, at . Variansen af estimatoren er derfor givet ved ρ² = ρ(1- ρ)/n, og standardafvigelsen er dermed givet ved ρ.

Ulovlige produkter i populationen, U

Antag, at antallet af ulovlige produkter i populationen er binomialfordelt med antalsparameter og sandsynlighedsparameter ρ, dvs. .

De statistiske egenskaber (middelværdi, varians og standardafvigelse) ved fordelingen for er givet ved:

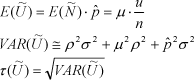
Formel

I beregningen af variansen udnyttes approksimationen, at for tilpas store n gælder det, at binomialfordelingen med parametre (n,ρ) ”ligner” normalfordelingen med parametre (nρ, nρ(1 - ρ)), og derefter anvendes formlen for varians af produktet af to normalfordelte variable..

| Til Top | | Forside |